Непрерывность элементарных функций
Теорема 4.7*. Всякая элементарная функция непрерывна в каждой точке, в которой она определена.
Докажем непрерывность некоторых из элементарных функций.
1. Функция 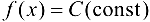 непрерывна для
непрерывна для 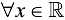 .
.
Действительно, 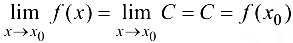 .
.
2. Функция 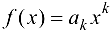 , где
, где 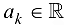 , непрерывна для
, непрерывна для 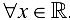 . Действительно,
. Действительно,
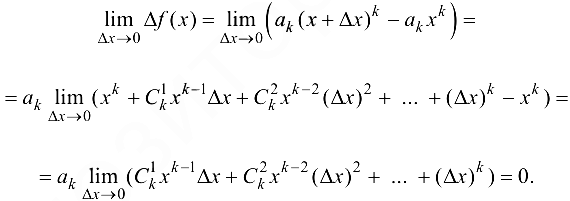
Тогда многочлен от 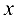 степени
степени 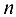
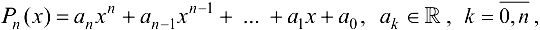
будет непрерывной функцией как сумма непрерывных функций вида 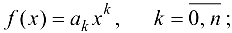 рациональная функция
рациональная функция 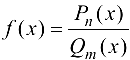 будет непрерывной функцией во всех точках, где
будет непрерывной функцией во всех точках, где 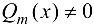 как отношение двух непрерывных функций.
как отношение двух непрерывных функций.
3. Функция 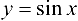 непрерывна на всей числовой прямой. Предварительно покажем, что
непрерывна на всей числовой прямой. Предварительно покажем, что 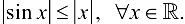 Действительно, (4.3) верно при
Действительно, (4.3) верно при 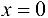 .
.
При 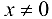 если
если 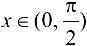 , то
, то 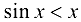 согласно доказательству первого замечательного предела; если
согласно доказательству первого замечательного предела; если 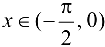 , то (4.3) будет выполнено, так как функция
, то (4.3) будет выполнено, так как функция 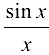 четная; если
четная; если 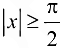 , то (4.3) верно, так как
, то (4.3) верно, так как 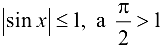 . Тогда
. Тогда
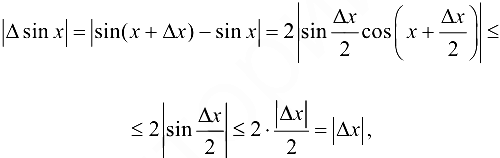
согласно (4.3), т. е. 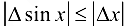 . Отсюда следует, что если
. Отсюда следует, что если 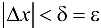 , то
, то 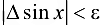 , т. е. функция
, т. е. функция 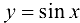 непрерывна на всей числовой прямой.
непрерывна на всей числовой прямой.
Аналогичным образом доказывается непрерывность функции 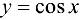 на всей числовой прямой.
на всей числовой прямой.
Функция 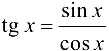 непрерывна в точках, где
непрерывна в точках, где 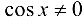 , т. е. в точках
, т. е. в точках 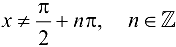 . Функция
. Функция 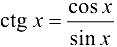 непрерывна в точках, где
непрерывна в точках, где 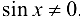 , т. е. в точках
, т. е. в точках 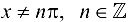 .
.
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:

