Функция
Пусть X и К — некоторые числовые множества.
Определение 1.1. Функцией называется множество 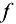 упорядоченных пар чисел
упорядоченных пар чисел 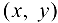 таких, что
таких, что 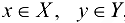 , и каждое
, и каждое 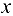 входит в одну и только одну пару этого множества, а каждое у входит по крайней мере в одну пару. При этом говорят, что числу х поставлено в соответствие число
входит в одну и только одну пару этого множества, а каждое у входит по крайней мере в одну пару. При этом говорят, что числу х поставлено в соответствие число 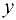 , и пишут
, и пишут 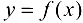 . Число у называется значением функции
. Число у называется значением функции 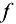 в точке
в точке 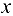 . Переменную у называют зависимой переменной, а переменную
. Переменную у называют зависимой переменной, а переменную 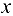 — независимой переменной (или существования); множество X — областью определения (или существования) функции (
— независимой переменной (или существования); множество X — областью определения (или существования) функции (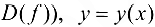 , а множество
, а множество 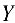 — множеством значений функции (
— множеством значений функции (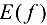 ).
).
Кроме буквы 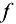 для обозначения функции используют и другие буквы, например:
для обозначения функции используют и другие буквы, например: 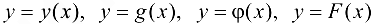 и т. д. Другими буквами могут обозначаться зависимая и независимая переменные. Иногда зависимую переменную также называют функцией.
и т. д. Другими буквами могут обозначаться зависимая и независимая переменные. Иногда зависимую переменную также называют функцией.
На плоскости функция изображается в виде графика — множества точек 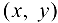 , координаты которых связаны соотношением
, координаты которых связаны соотношением 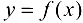 , называемым уравнением графика.
, называемым уравнением графика.
График функции может представлять собой некоторую «сплошную» линию (кривую или прямую), может состоять из отдельных точек, например график функции 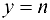 !
!
Заметим, что не всякая линия является графиком какой-либо функции. Например, окружность 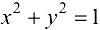 не является графиком функции, так как каждое значение
не является графиком функции, так как каждое значение 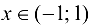 входит не в одну, а в две пары чисел
входит не в одну, а в две пары чисел 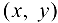 этого множества с разными значениями
этого множества с разными значениями 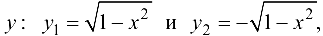 что противоречит требованию однозначности в определении функции. Однако часть окружности, лежащая в нижней полуплоскости, является графиком функции
что противоречит требованию однозначности в определении функции. Однако часть окружности, лежащая в нижней полуплоскости, является графиком функции 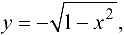 , а другая ее часть, лежащая в верхней полуплоскости, — графиком функции
, а другая ее часть, лежащая в верхней полуплоскости, — графиком функции 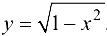 .
.
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:
| Грани числовых множеств |
| Предельные точки числового множества |
| Способы задания функций с примерами |
| Основные характеристики функции |

