Пример задачи 5.15
Определить угол поворота и прогиб сечения В консольной балки (в долях от жесткости сечения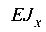 
), рис. 5.28.
Решение
Эпюра изгибающих моментов от заданной нагрузки (грузовая эпюра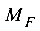 
) показана на рис. 5.28, а.
Для определения прогиба в сечении В к свободной от заданной нагрузки балке (вспомогательное состояние) в названном сечении прикладывается вспомогательная единичная сосредоточенная сила (F = 1) и строится эпюра изгибающих моментов — единичная эпюра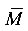 
(рис. 5.28, б). Единичная сила направляется произвольно, т. е. в положительном или отрицательном направлении оси У.
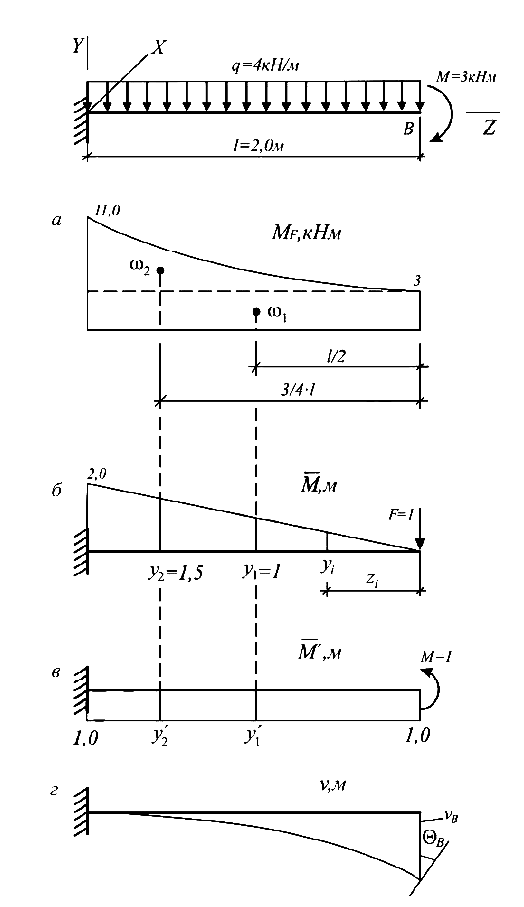
Аналогичная операция производится для определения угла поворота сечения. Только в качестве вспомогательной единичной силы выступает единичный вспомогательный момент (М = 1), направляемый произвольно относительно оси X. Эпюра от единичного момента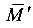 
показана на рис. 5.28, в.
На рис. 5.28, б и в схема балки и единичные эпюры совмещены. Заметим, что балка имеет один расчетный участок как для ,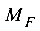
так для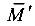 
и что единичные эпюры прямолинейны и имеют вид треугольника или прямоугольника, а грузовая — криволинейна и имеет сложное очертание.
Для определения перемещений по способу Верещагина используются эпюры изгибающих моментов (грузовые и единичные). От одних из них берутся площади эпюр (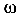
), из других — ординаты (у) под центром тяжести первых. Поскольку грузовая эпюра 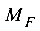имеет криволинейное очертание, площадь 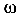должна браться с этой эпюры.
Для проведения расчета эпюра 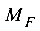сложного очертания делится на простые фигуры: прямоугольник (от момента М) площадью
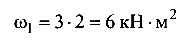
и параболический треугольник (от нагрузки q) площадью
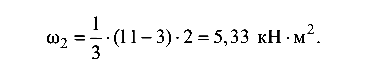
На выделенных простых фигурах отмечаются их центры тяжести (см. табл. 5.1).
На единичных эпюрах отмечаются ординаты у, лежащие под центром тяжести составляющих частей грузовой эпюры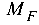 
. В данном примере ордината определяется как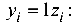 
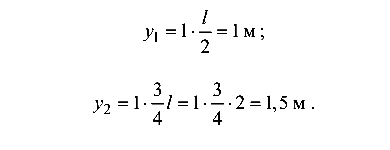
Для определения углов поворота сечений ординаты берутся из единичной эпюры :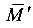
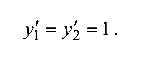
Прогиб в сечении В по формуле (5.12):
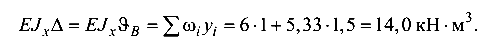
Все слагаемые в выражении прогибов положительны, так как площади 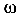и ординаты у лежат по одну сторону от оси эпюры. Положительные значения 
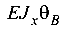означают, что прогиб происходит в направлении единичной силы, т. е. вниз.
Угол поворота сечения В
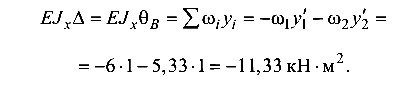
В полученном выражении слагаемые отрицательны, так как площади 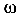и ординаты у лежат по разную сторону от оси эпюры. Отрицательное значение 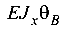означает, что поворот сечения происходит в направлении, противоположном направлению единичного момента, т. е. по ходу часовой стрелки (рис. 5.28, г).
Эпюра прогибов показана на рис. 5.28, г.
Таким образом, перемещения на свободном конце балки (в долях от жесткости сечения)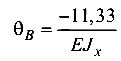 
(по ходу часовой стрелки),
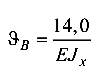(вниз).
Этот пример решения задачи взят со страницы решения задач с примерами по всем темам предмета «Сопротивление материалов»:
Примеры решения задач по сопротивлению материалов
Дополнительные задачи которые вам будут полезны:
