Пример задачи 5.11
Для консольной балки определить углы поворота и прогибы сечений В и С (в долях от жесткости сечения балки — 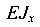 ), рис. 5.22.
), рис. 5.22.
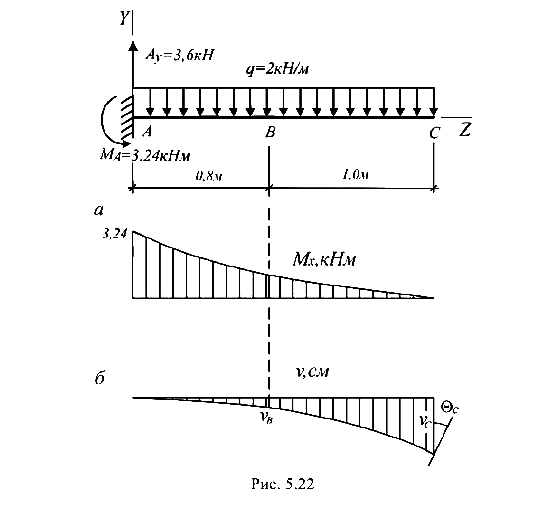
Начало координатных осей помещаем в крайнем левом сечении балки (защемлении).
Опорные реакции определяются из условий равновесия:
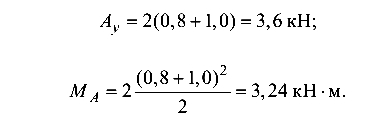
Балка имеет один расчетный участок. Эпюра изгибающих моментов показана на рис. 5.22, а. Составим уравнения оси изогнутой балки по формулам (5.9) и (5.10).
Уравнение углов поворота сечений
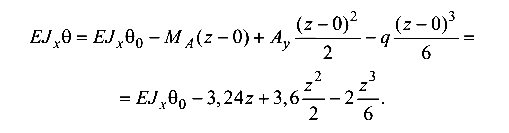
Уравнение прогибов
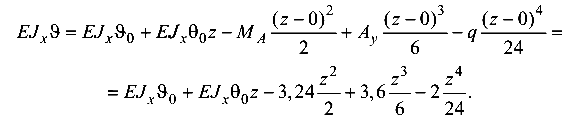
Заметим, что слагаемыми уравнений являются выражения изгибающих моментов (с их знаками) от соответствующих силовых факторов (например, 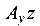 ), проинтегрированные в уравнении углов поворота сечений один раз
), проинтегрированные в уравнении углов поворота сечений один раз 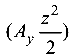 , а в уравнении прогибов — два раза
, а в уравнении прогибов — два раза 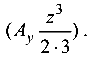
Начальные параметры (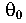 и
и 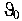 в составленных уравнениях определяются исходя из деформативных условий в начале координат.
в составленных уравнениях определяются исходя из деформативных условий в начале координат.
Поскольку начало координат помещено на опоре А — защемлении, где невозможны ни линейные, ни угловые перемещения, начальные параметры 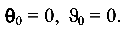
Уравнения перемещений оси балки примут вид
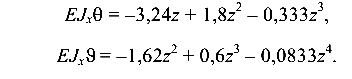
Определяем перемещения в названных сечениях. При z = 0,8 м (сечение В)
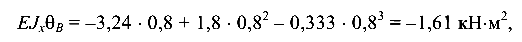
— откуда угол поворота сечения 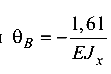 (направлен по ходу часовой стрелки);
(направлен по ходу часовой стрелки);
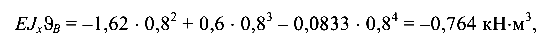
откуда прогиб 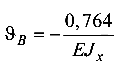 (направлен вниз от оси Z).
(направлен вниз от оси Z).
При z = 1,8 м (сечение С)

откуда 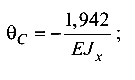
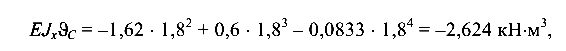
откуда прогиб 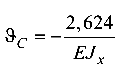 (направлен вниз).
(направлен вниз).
По вычисленным значениям можно построить эпюры углов поворота сечений 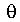 и прогибов
и прогибов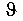 . Эпюра
. Эпюра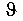 показана на рис. 5.22, б, где отмечен также угол
показана на рис. 5.22, б, где отмечен также угол 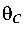 . Полностью эпюра
. Полностью эпюра 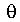 строится редко.
строится редко.
Результаты вычислений показывают, что в данном примере наибольшие перемещения претерпевает концевое сечение балки (сечение С).
Эпюра изгибающих моментов 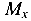 и эпюра прогибов
и эпюра прогибов 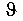 связаны между собой следующей зависимостью: ординаты эпюры
связаны между собой следующей зависимостью: ординаты эпюры 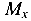 должны лежать с выпуклой стороны изогнутой балки, где волокна ее растянуты. В строительном проектировании эпюру
должны лежать с выпуклой стороны изогнутой балки, где волокна ее растянуты. В строительном проектировании эпюру 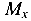 принято строить со стороны растянутых волокон.
принято строить со стороны растянутых волокон.
Этот пример решения задачи взят со страницы решения задач с примерами по всем темам предмета «Сопротивление материалов»:
Примеры решения задач по сопротивлению материалов
Дополнительные задачи которые вам будут полезны:
