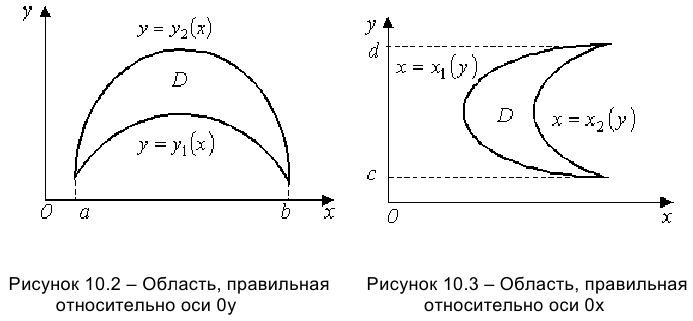
Область  называется правильной относительно оси
называется правильной относительно оси 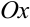 , если прямая, параллельная этой оси, проходящая через внутреннюю точку области
, если прямая, параллельная этой оси, проходящая через внутреннюю точку области  , пересекает границу области в двух точках. Аналогично определяется правильная область относительно оси
, пересекает границу области в двух точках. Аналогично определяется правильная область относительно оси 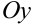 .
.
Область  , правильную относительно как
, правильную относительно как 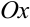 , так и
, так и 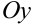 , называют просто правильной областью.
, называют просто правильной областью.
Если область  — правильная относительно
— правильная относительно 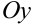 (рисунок 10.2), двойной интеграл вычисляется по формуле:
(рисунок 10.2), двойной интеграл вычисляется по формуле:
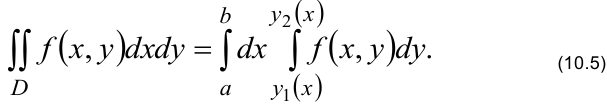
Правую часть формулы (10.5) называют повторным (двукратным)
интегралом.
Вычисление повторного интеграла начинаем с вычисления внутреннего интеграла 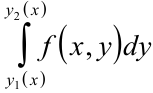 в котором переменную
в котором переменную 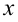 надо принять при интегрировании за постоянную величину. После подстановки пределов интегрирования в первообразную получаем некоторую функцию от
надо принять при интегрировании за постоянную величину. После подстановки пределов интегрирования в первообразную получаем некоторую функцию от 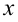 , которую затем интегрируем на отрезке
, которую затем интегрируем на отрезке 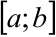 .
.
Если область  является правильной относительно оси
является правильной относительно оси 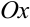 (рисунок 10.3), двойной интеграл вычисляется по формуле:
(рисунок 10.3), двойной интеграл вычисляется по формуле:
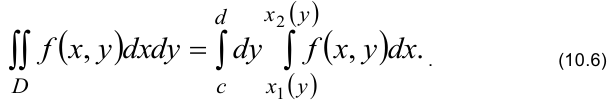
Если область  — просто правильная, можно применять как формулу (10.5), так и формулу (10.6). При этом переход от одной формулы к другой называют изменением порядка интегрирования.
— просто правильная, можно применять как формулу (10.5), так и формулу (10.6). При этом переход от одной формулы к другой называют изменением порядка интегрирования.
Сам процесс перехода от двойного интеграла к повторному и расстановка пределов интегрирования для внешнего и внутреннего интегралов называют приведением двойного интеграла к повторному.
Правило расстановки пределов:
- В пределах внутреннего интеграла (интеграла по первой переменной) в общем случае стоят функции второй переменной.
- В пределах внешнего интеграла (по второй переменной) стоят постоянные числа.
В результате вычисления двойного интеграла получается некоторое постоянное число.
Если область не является правильной ни относительно оси 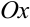 , ни относительно оси
, ни относительно оси 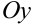 , её разбивают на конечное число областей
, её разбивают на конечное число областей 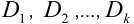 , правильных относительно одной из осей и при вычислении применяют свойство 2.
, правильных относительно одной из осей и при вычислении применяют свойство 2.
Пример выполнения задания
Изобразить на плоскости область интегрирования  . Вычислить двойной интеграл
. Вычислить двойной интеграл 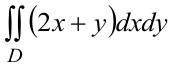 . Граница области
. Граница области  задана уравнениями:
задана уравнениями:
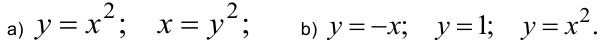
Решение:
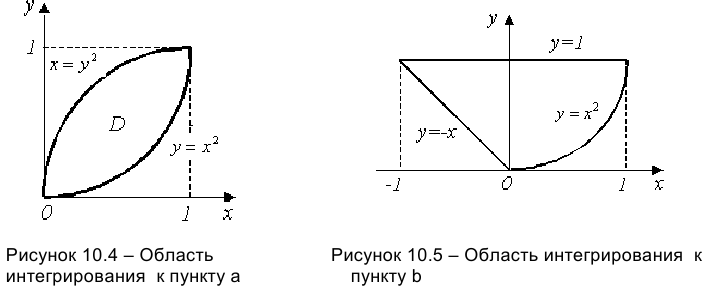
а) Построив кривые, получим область  (рисунок 10.4). Область правильная. Применим формулу (10.5). При этом уравнение верхней границы области
(рисунок 10.4). Область правильная. Применим формулу (10.5). При этом уравнение верхней границы области 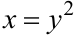 преобразуем к виду
преобразуем к виду 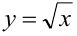 :
:
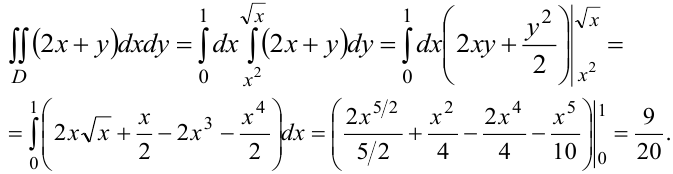
Изменим порядок интегрирования и применим формулу (10.6):
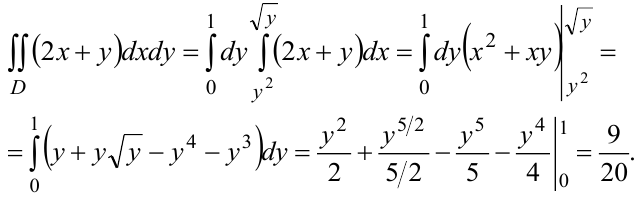
b) Область  построена на рисунке 10.5. Область
построена на рисунке 10.5. Область  правильная. Выбираем для интегрирования формулу (10.6):
правильная. Выбираем для интегрирования формулу (10.6):
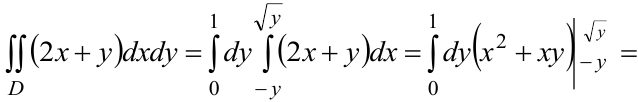
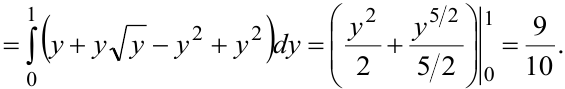
Изменим порядок интегрирования. При этом нижняя граница области  задана двумя аналитическими выражениями
задана двумя аналитическими выражениями 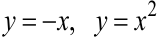 . В этом случае область
. В этом случае область  нужно разбить на две области
нужно разбить на две области 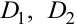 с помощью прямой, проходящей по оси
с помощью прямой, проходящей по оси 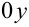 . На основании свойства 2 двойного интеграла получаем:
. На основании свойства 2 двойного интеграла получаем:
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:

