Оглавление:
Уравнение вида:
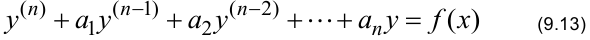
называется линейным неоднородным дифференциальным, сокращенно ЛНДУ. Соответствующее ему однородное уравнение имеет вид:
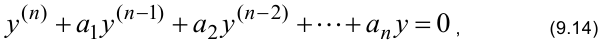
Общее решение неоднородного линейного уравнения есть сумма общего решения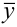 
однородного уравнения, соответствующего данному неоднородному, и частного решения неоднородного уравнения 
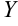. С учетом формулы (9.10) общее решение ЛНДУ имеет вид:
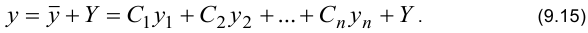
Формула (9.15) определяет структуру общего решения ЛНДУ.
Неоднородные линейные уравнения со специальной правой частью
Если найдена фундаментальная система решений ЛОДУ, то для любой правой части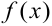 
ЛНДУ частное решение 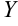можно определить интегрированием.
Если неоднородное линейное уравнение имеет правую часть 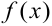определенного вида, рассматриваемого ниже, то частное решение 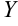можно определить, не прибегая к методу интегрирования. Рассматривается два вида правой части, которые называются специальными.
1) Правая часть вида
где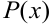 
— многочлен степени 
.
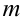Частное решение нужно искать в виде
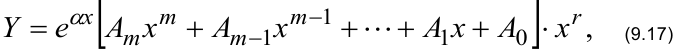
где неизвестные заранее коэффициенты 
определяются методом неопределенных коэффициентов, показатель 
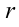равен количеству корней характеристического уравнения, равных коэффициенту в показателе экспоненты.
2) Правая часть вида
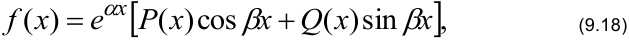
где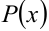 
, 
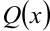— многочлены по степеням 
.
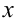Частное решение нужно искать в виде
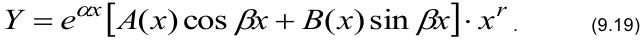
При этом многочлены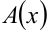 
и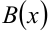 
должны быть одинаковой степени, большей из степеней многочленов 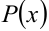и 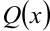. Показатель 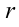равен количеству пар комплексных сопряженных корней характеристического уравнения, у которых действительная часть совпадает с коэффициентом в показателе экспоненты 
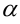, а мнимая — с коэффициентом 
.
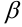Многочлены 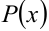и 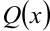в формулах (9.16) и (9.18) могут не содержать некоторых степеней 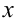. Частное решение (9.17) и (9.19) должно содержать многочлены той же степени со всеми коэффициентами.
Наличие в правой части (9.16) многочлена без экспоненты говорит о том, что показатель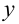 
экспоненты равен нулю, и для определения числа 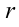в формуле (9.17) проверяют наличие нулевых корней характеристического уравнения.
Правая часть (9.18) может содержать только одну из функци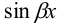й 
или 
, но частное решение (9.19) должно записываться с обеими этими функциями.
Коэффициенты многочленов 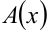и 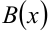определяются методом неопределенных коэффициентов.
Метод неопределенных коэффициентов основан на том, что любое решение дифференциального уравнения превращает его в тождество. Если решение 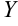подставить в данное ЛНДУ, уравнение превратится в тождество, в котором при одинаковых функциях левой и правой части должны стоять одинаковые коэффициенты. Приравнивая коэффициенты при одинаковых степенях 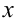или других функциях, получаем систему уравнений относительно неизвестных коэффициентов в многочленах 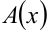и .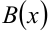
Пример 9.7
Найти общее решение ЛНДУ: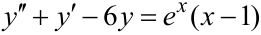 
.
Решение:
Вначале определяется общее решение соответствующего ЛОДУ (см. пример 9.5в):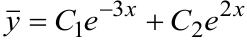 
. Далее находим частное решение ЛНДУ. Коэффициент в показателе экспоненты в правой части не равен корню характеристического уравнения, следовательно, 
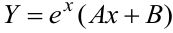. Для нахождения неизвестных 
, 
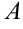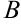применяем метод неопределенных коэффициентов.
Подставим 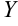в заданное уравнение. Для этого нужно найти 
.
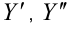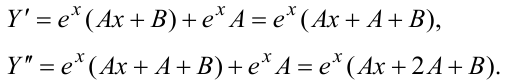
Подставляя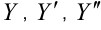 
в уравнение, получаем
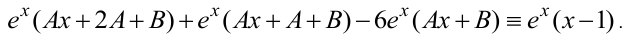
Разделим тождество на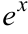 
, а затем приравняем коэффициенты при
одинаковых степенях :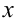
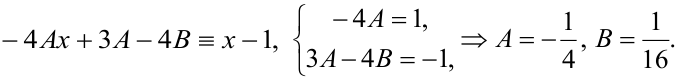
Следовательно, искомое общее решение записывается как
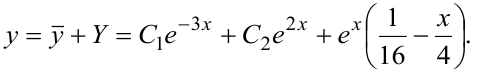
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
| Линейные уравнения первого порядка |
| Задача Коши для уравнения 1-го порядка |
| Двойной интеграл. Объём цилиндрического тела |
| Основные свойства и приложения двойного интеграла |
