Частные производные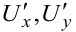 
от функции 
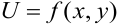определяют скорость изменения функции в направлении осей 
, 
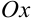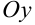. Если требуется знать скорость изменения функции в заданной точке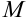 
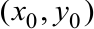в направлении, образующем угол 
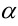с осью 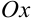, то эта задача решается нахождением производной по направлению.
Определение. Производной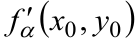 
функции 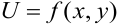в точке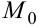 
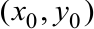направлении 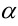называется предел отношения приращения 
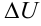функции, возникшего при перемещении точки 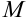из положения 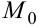вдоль луча, составляющего угол 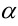с положительным направлением оси 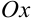, к величине 
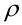такого перемещения, когда 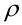стремится к нулю.
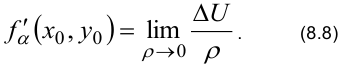
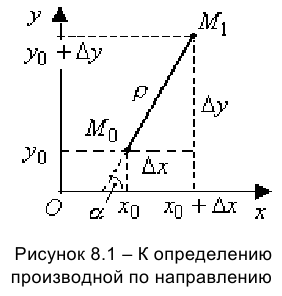
Из рисунка 7.1 следует, что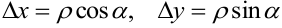 
. Используя эквивалентность полного приращения функции и полного дифференциала, из определения производной по направлению получим:
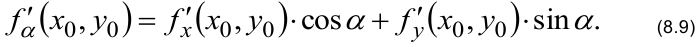
Пример:
Вычислить в точке 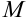(1;2) производную от функции 
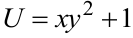в направлении, составляющем угол 
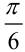с осью .
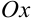Решение:
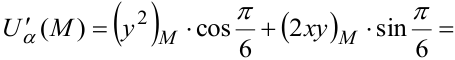
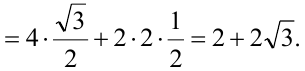
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
