Оглавление:
Понятие несобственного интеграла является обобщением понятия определенного интеграла от непрерывной функции на конечном отрезке.
Интегралы с бесконечными пределами
Пусть функция 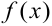 определена и непрерывна при всех значениях аргумента
определена и непрерывна при всех значениях аргумента 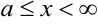 . Для такого бесконечного интервала понятие интегральной суммы не определено.
. Для такого бесконечного интервала понятие интегральной суммы не определено.
Если существует конечный предел от интеграла с переменным верхним пределом
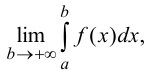
то он называется несобственным интегралом от функции 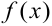 на интервале
на интервале 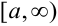 и обозначается интегралом, в верхнем пределе которого стоит знак бесконечности:
и обозначается интегралом, в верхнем пределе которого стоит знак бесконечности:
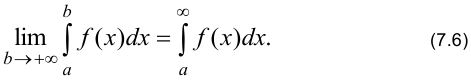
В этом случае несобственный интеграл существует (сходится). Если не существует конечного предела (7.6), то несобственный интеграл не существует (расходится).
Аналогично определяются несобственный интеграл с бесконечным нижним пределом и несобственный интеграл с бесконечными верхним и нижним пределами:
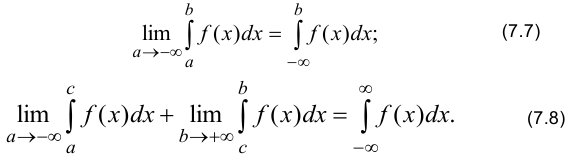
Формулы (7.6), (7.7), (7.8) кроме определения несобственного интеграла показывают способ его вычисления.
Интегралы от разрывных функций
Пусть функция 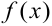 определена и непрерывна при
определена и непрерывна при 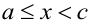 , а при
, а при 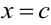 либо не определена, либо терпит разрыв. В этом случае нельзя говорить об интеграле
либо не определена, либо терпит разрыв. В этом случае нельзя говорить об интеграле
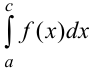
как о пределе интегральных сумм, так как функция 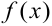 не является непрерывной на интервале
не является непрерывной на интервале 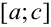 .
.
Если существует конечный предел интеграла от разрывной при 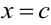 функции, то он называется несобственным сходящимся интегралом:
функции, то он называется несобственным сходящимся интегралом:
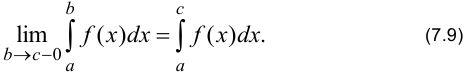
В противном случае интеграл называется расходящимся.
Если функция имеет разрыв при 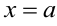 , то по определению
, то по определению
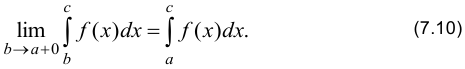
Если функция имеет разрыв при  , где точка с лежит внутри интервала интегрирования
, где точка с лежит внутри интервала интегрирования  , то
, то
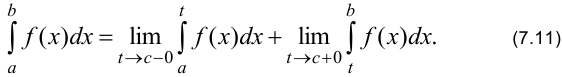
Пример:
Вычислить несобственные интегралы и установить их сходимость: a) 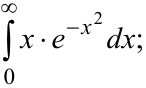 б)
б) 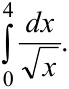
Решение:
а) Интеграл с бесконечным верхним пределом вычисляем по формуле (7.6):
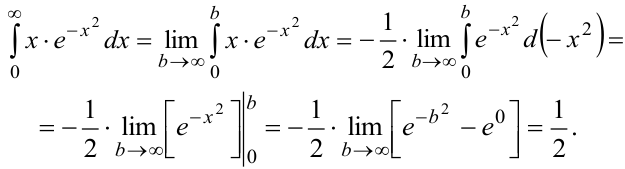
Интеграл сходится.
б) Несобственный интеграл имеет разрыв в нижнем пределе интегрирования функции, интеграл вычисляем по формуле (7.10):
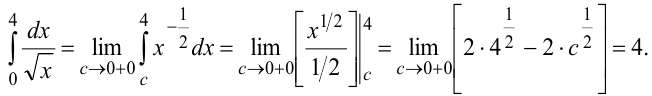
Интеграл сходится.
О функциях, интегралы от которых не выражаются через элементарные функции
По сути вопроса можно сказать следующее:
- во-первых, всякая непрерывная на отрезке функция имеет на нем первообразную;
- во-вторых, не всякая первообразная может быть выражена комбинацией конечного числа элементарных функций.
Такие первообразные выражены интегралами 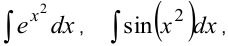
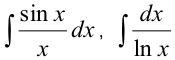 и многими другими.
и многими другими.
Применение формулы Ньютона — Лейбница в случае «не берущихся» интегралов затруднительно.
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:

