Оглавление:
Метод табличного (непосредственного) интегрирования заключается в том, что с помощью эквивалентных преобразований подынтегральной функции и на основании свойств неопределённого интеграла заданные интегралы преобразуются в табличные.
Пример №1
Найти неопределённый интеграл
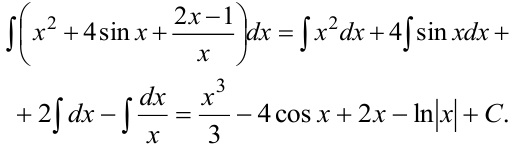
При интегрировании были использованы свойства №3, 4, 5 неопределённого интеграла и табличные интегралы №1,2, 5.
Значения интегралов от основных элементарных функций получены на основе формул дифференцирования.
Таблица 3 — Таблица интегралов

Из свойств дифференциала вытекает, что 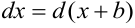 и
и 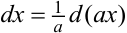 , где
, где 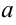 и
и 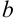 — постоянные величины. Поэтому из свойства №6 неопределенного интеграла следуют формулы, полезные при нахождении неопределенных интегралов: если
— постоянные величины. Поэтому из свойства №6 неопределенного интеграла следуют формулы, полезные при нахождении неопределенных интегралов: если 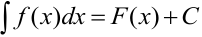 , то
, то
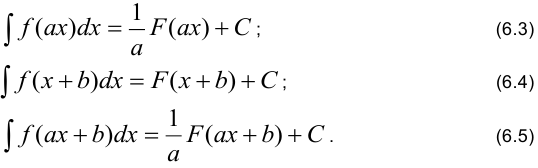
Пример №2
Найти неопределённые интегралы
a) 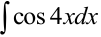 ;
;
б)  .
.
Решение:
а) По формуле (6.3):  , так как
, так как  .
.
б) По формуле (6.5)  , так как
, так как 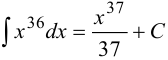 .
.
Пример №3
Методом непосредственного интегрирования найти неопределенный интеграл:
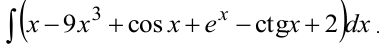
Решение:
Заданный интеграл от суммы функций записываем суммой интегралов, при этом постоянные множители выносим за знак интегралов.
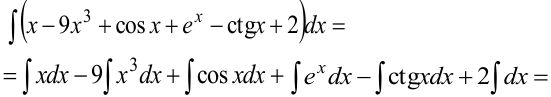
= (для каждого интеграла определяем первообразную по таблице 3) =

Произвольная постоянная 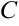 проставляется после определения всех первообразных.
проставляется после определения всех первообразных.
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
| Применение 1-й и 2-й производной для исследования функций |
| Первообразная. Неопределённый интеграл и его свойства |
| Интегрирование по частям |
| Интегрирование подстановкой |

