Рассмотрим функцию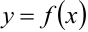 
. По определению производной 
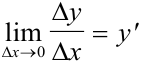. Откуда 
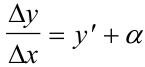, где 
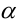— бесконечно малая при 
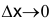, т.е. 
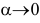. Умножим последнее равенство на 
:
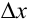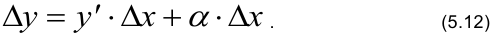
В правой части равенства (5.12) слагаемое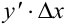 
— бесконечно малая низшего порядка малости по сравнению со слагаемым 
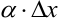, оно считается главной частью приращения функции 
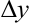и называется дифференциалом функции, что обозначается так:
Из формулы (5.13) следует, что производную можно обозначить как отношение дифференциала функции к дифференциалу аргумента:
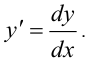
Свойства дифференциала
- Дифференциал аргумента равен его приращению.
- Дифференциал функции эквивалентен приращению функции при 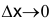, т.е.
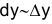. - Дифференциал функции вычисляется по формуле (5.13), где
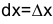. - Свойство инвариантности формы дифференциала заключается в том, что дифференциал сложной функции имеет тот же вид, какой он имел бы в том случае, если бы промежуточный аргумент и был независимой переменной: если
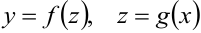, то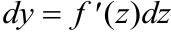 
. - Так как задача нахождения дифференциала равносильна нахождению производной, то правила дифференцирования функций сохраняют свою силу и для дифференциала, а именно:
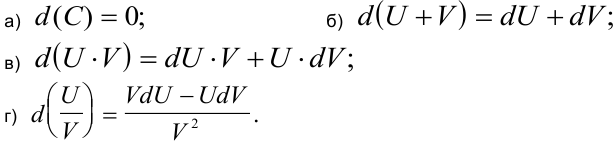
Дифференциал функции находит применение в приближённых вычислениях, основанных на формуле
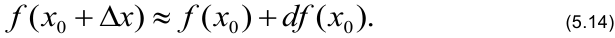
Формула следует из эквивалентности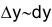 
.
Если известно значение функции при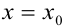 
, то, используя (5.14) легко найти значение функции при 
.
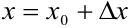Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
