Оглавление:
Если два вектора перемножаются по векторному произведению и результат скалярно умножается на третий вектор, то такое произведение векторов называется смешанным.
Свойства смешанного произведения
1. При круговой перестановке сомножителей произведение не изменяется:
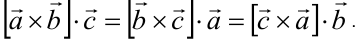
2. Смешанное произведение не изменится, если поменять местами знаки векторного и скалярного произведений: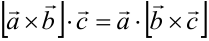 
.
Это позволяет записывать смешанное произведение векторов вообще без знаков умножения: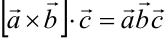 
. В дальнейшем смешанное произведение трёх векторов будет записываться без знаков умножения.
3. При перестановке двух сомножителей знак произведения меняется на противоположный.
4. Смешанное произведение равно нулю, если:
а) один из векторов нулевой;
б) два вектора коллинеарные;
в) три вектора компланарные.
Смешанное произведение вычисляется как определитель, составленный из координат векторов
Геометрический смысл смешанного произведения состоит в том, что его модуль равен объёму параллелепипеда, построенного на векторах, как на рёбрах.
При этом если тройка векторов правая, то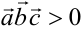 
, если тройка векторов левая, то 
.
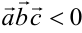Если на тех же векторах строить не параллелепипед, а треугольную пирамиду — тетраэдр, то его объём вычисляется по формуле
На формулах (3.12) и (3.14) основано решение задания 4.
На свойстве 4 смешанного произведения и формуле (3.12) основано условие компланарности трёх векторов:
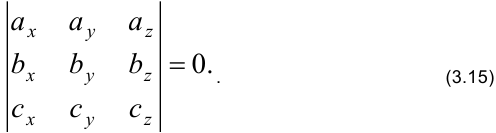
Пример выполнения задания
Пример:
Вычислить объём треугольной пирамиды с вершинами в точках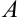 
(0,0,1), 
(2,3,5),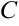 
(6,2,3), 
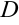(3,7,2).
Решение:
Найдём векторы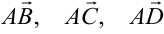 
, совпадающие с рёбрами пирамиды и выходящие из точки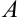
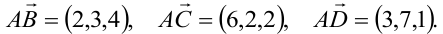
В фигурных скобках записаны компоненты векторов. Обозначим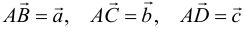 
. Применяем формулу (3.12), затем (3.14).
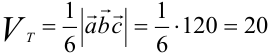(куб. ед.)
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
