Оглавление:
Векторным произведением двух векторов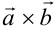 
называется третий вектор 
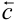, длина которого равна
Вектор 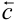перпендикулярен векторам 
, 
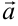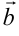(следовательно, перпендикулярен плоскости этих векторов) и направлен так, что тройка векторов — правая, т.е. из конца вектора 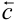видно, что поворот вектора 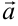до совмещения с вектором 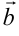по кратчайшему пути происходит против часовой стрелки.
Свойства векторного произведения
- При перестановке сомножителей знак векторного произведения меняется на противоположный.
- Скалярный множитель выносится за знак векторного произведения.
- Векторное произведение равно нулевому вектору, если один из векторов нулевой или векторы коллинеарные.
Векторное произведение вычисляется по формуле:
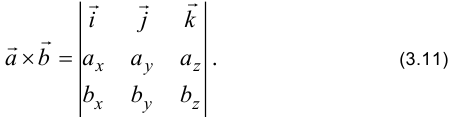
Правая часть формулы — определитель 3-го порядка, вычисляемый по формуле (1.4). Теперь этот определитель — выражение, а не число, так как элементами определителя служат и числа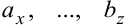 
и орты 
.
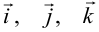Из формулы (3.10) следует, что модуль векторного произведения численно равен площади параллелограмма, построенного на векторах, как на сторонах. Площадь треугольника, построенного на этих векторах, равна половине площади параллелограмма. На этом факте основано задание 3.
Пример выполнения задания
Пример:
Вычислить площадь треугольника с вершинами в точках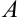 
(2,2,2), 
(4,0,3),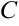 
(0,1,0).
Решение:
Площадь треугольника, построенного на векторах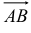 
, 
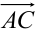равна половине модуля их векторного произведения
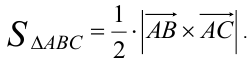
Находим векторы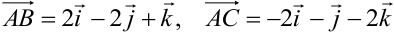 
.
Находим векторное произведение по формуле (3.11)
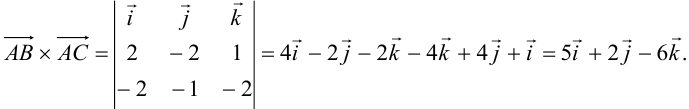
Модуль вектора определяем по формуле (3.2)
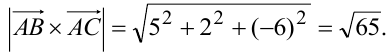
Ответ: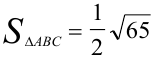 
(кв. ед.).
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
