Минором 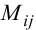 элемента
элемента 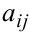 данного определителя называется определитель, полученный из данного путём вычёркивания строки и столбца, на пересечении которых стоит элемент
данного определителя называется определитель, полученный из данного путём вычёркивания строки и столбца, на пересечении которых стоит элемент 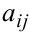 . Здесь
. Здесь 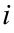 — номер строки,
— номер строки, 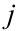 — номер столбца.
— номер столбца.
Например, для элемента 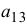 определителя (1.4) минор имеет вид:
определителя (1.4) минор имеет вид:
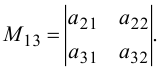
Алгебраическим дополнением 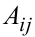 элемента
элемента 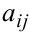 называется минор этого элемента, умноженный на (-1) в степени, равной сумме номеров строки и столбца:
называется минор этого элемента, умноженный на (-1) в степени, равной сумме номеров строки и столбца:

Каждый определитель может быть вычислен как сумма произведений элементов какого-либо ряда на их алгебраические дополнения:
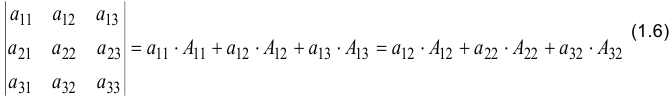
Здесь приведено вычисление определителя в двух вариантах: по элементам первой строки и по элементам второго столбца.
Формула (1.6) называется разложением определителя по элементам ряда.
Примечание — сумма произведений элементов одного ряда на алгебраические дополнения параллельного ряда всегда равна нулю. В этом легко убедиться на примере определителя второго порядка 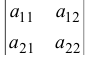 .
.
Для него 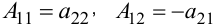 .
.
Тогда 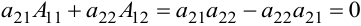 .
.
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
| Операции с матрицами: определения и пример с решением |
| Определители 2 и 3 порядков, вычисление, свойства |
| Обратная матрица, её вычисление |
| Решение определенных систем с помощью обратной матрицы |
