Оглавление:
Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью
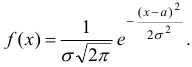
Нормальное распределение определяется двумя параметрами: 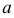 — математическим ожиданием,
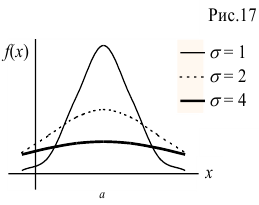
— математическим ожиданием, 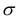 — средне квадратическим отклонением нормального распределения. График плотности нормального распределения (кривая Гаусса) для значений
— средне квадратическим отклонением нормального распределения. График плотности нормального распределения (кривая Гаусса) для значений 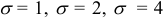 показан на рис. 17. Рассматривая эти кривые, видим, что чем меньше
показан на рис. 17. Рассматривая эти кривые, видим, что чем меньше 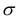 , тем максимум функции
, тем максимум функции 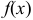 больше, а рассеивание значений случайной величины относительно математического ожидания
больше, а рассеивание значений случайной величины относительно математического ожидания 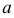 меньше.
меньше.
Вероятность того, что случайная величина, распределенная по нормальному закону, примет значение, принадлежащее интервалу 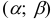 , определяется формулой
, определяется формулой
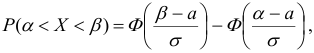
где 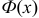 — функция Лапласа.
— функция Лапласа.
Правило трех сигм
Если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения, а именно: 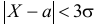 .
.
Теорема Ляпунова (центральная предельная теорема)
Если случайная величина 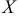 представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю суму ничтожно мало, то
представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю суму ничтожно мало, то 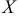 имеет распределение близкое к нормальному.
имеет распределение близкое к нормальному.
Из этой теоремы следует, что нормально распределенные случайные величины широко распространены на практике.
При изучении распределений, отличных от нормального, возникает необходимость количественно оценить это различие. С этой целью вводят специальные характеристики, в частности асимметрию и эксцесс.
Асимметрией теоретического распределения называют отношение центрального момента третьего порядка к кубу средне квадратического отклонения:
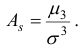
Если длинная часть кривой расположена правее моды 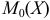 (точки максимума функции), то асимметрия положительна (рис. 18(a)), если слева — отрицательна (рис. 18(б)).
(точки максимума функции), то асимметрия положительна (рис. 18(a)), если слева — отрицательна (рис. 18(б)).
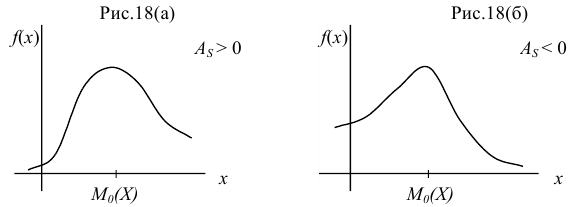
Эксцессом теоретического распределения называют характеристику, которая определяется равенством 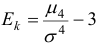 .
.
Эксцесс нормального распределения равен нулю.
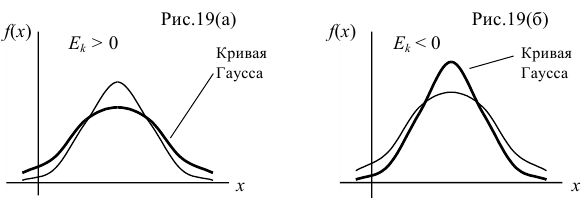
Если эксцесс некоторого распределения отличен от нуля, то кривая этого распределения отличается от нормальной кривой: если 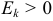 , то кривая имеет более высокую и острую вершину, чем нормальная кривая (рис. 19(a)); если
, то кривая имеет более высокую и острую вершину, чем нормальная кривая (рис. 19(a)); если 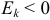 , то кривая имеет более низкую и плоскую вершину, чем нормальная кривая (рис. 19(б)). При этом предполагается, что нормальное и теоретическое распределения имеют одинаковые математические ожидания и дисперсии.
, то кривая имеет более низкую и плоскую вершину, чем нормальная кривая (рис. 19(б)). При этом предполагается, что нормальное и теоретическое распределения имеют одинаковые математические ожидания и дисперсии.
Пример:
Математическое ожидание 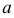 и среднее квадратическое отклонение
и среднее квадратическое отклонение 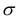 нормально распределенной величины
нормально распределенной величины 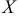 соответственно равны 5 и 2. Найти вероятность попадания этой величины в заданный интервал (3; 8).
соответственно равны 5 и 2. Найти вероятность попадания этой величины в заданный интервал (3; 8).
Решение:
Воспользуемся формулой 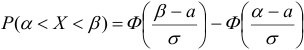 , где
, где 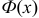 — функция Лапласа. Подставив
— функция Лапласа. Подставив 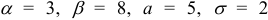 , получим
, получим 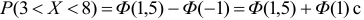 с учетом того, что функция Лапласа
с учетом того, что функция Лапласа 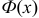 нечетна:
нечетна: 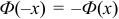 . По таблице приложения находим:
. По таблице приложения находим: 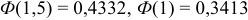 . Искомая вероятность
. Искомая вероятность 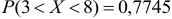 .
.
На этой странице размещён краткий курс лекций по теории вероятностей и математической статистике с теорией, формулами и примерами решения задач:
Теория вероятностей краткий курс для школьников и студентов
Возможно вам будут полезны эти страницы:

