Оглавление:
Определение 1. Двумерной 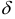 — окрестностью точки
— окрестностью точки 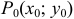 называется множество точек
называется множество точек 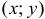 , принадлежащих открытому кругу радиуса
, принадлежащих открытому кругу радиуса 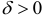 с центром в точке
с центром в точке 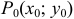 и обозначается
и обозначается 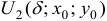 .
.
Если при фиксированном числе 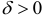 точка
точка 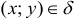 — окрестности (символика
— окрестности (символика 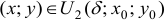 ), то говорят, что точка
), то говорят, что точка 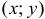 близка к точке
близка к точке 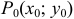 . Если точка
. Если точка 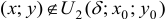 , то говорят, что точка
, то говорят, что точка 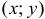 далека от точки
далека от точки 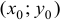 .
.
Если точка 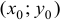 принадлежит множеству
принадлежит множеству 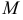 вместе со своей
вместе со своей 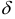 — окрестностью
— окрестностью 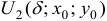 , т.е. со всеми своими близкими точками
, т.е. со всеми своими близкими точками 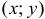 , то она (точка
, то она (точка 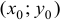 ) называется внутренней точкой множества
) называется внутренней точкой множества 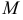 .
.
Определение 2. Точка 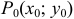 называется точкой локального максимума (минимума) функции
называется точкой локального максимума (минимума) функции 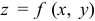 , если для всех точек
, если для всех точек 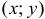 из области определения функции, близких к точке
из области определения функции, близких к точке 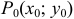 выполняется неравенство
выполняется неравенство 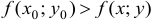 (соответственно,
(соответственно, 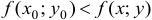 ).
).
Значение функции 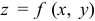 в точке максимума (минимума) называется максимумом (минимумом) функции.
в точке максимума (минимума) называется максимумом (минимумом) функции.
Если точка 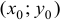 — точка локального максимума (минимума) функции
— точка локального максимума (минимума) функции 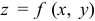 , то около точки
, то около точки 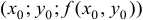 трехмерного пространства график функции
трехмерного пространства график функции 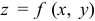 имеет вид «шапочки» (соответственно, перевернутой «шапочки») см. рис.
имеет вид «шапочки» (соответственно, перевернутой «шапочки») см. рис.
Слова «максимум» и «минимум» можно заменить одним «экстремум». Аналогично определяется экстремум функции трех и большего числа переменных.
Экстремум функции нескольких переменных может достигаться лишь в точках, лежащих внутри области ее определения, в которых все частные производные первого порядка обращаются в нуль. Такие точки называются стационарными. Для функции двух переменных 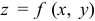 стационарные точки находятся из системы уравнений:
стационарные точки находятся из системы уравнений:

Условия (1) являются необходимыми условиями существования экстремума.
Достаточные условия экстремума для функции 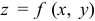 выражаются с помощью определителя
выражаются с помощью определителя 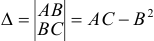 .
.
где 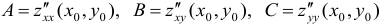 , а именно:
, а именно:
1) если 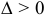 , то
, то 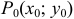 — точка экстремума: при
— точка экстремума: при 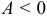 (или
(или 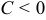 ) — точка максимума, при
) — точка максимума, при 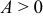 ( или
( или 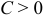 ) — точка минимума.
) — точка минимума.
2) если 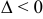 , то в точке
, то в точке 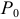 нет экстремума.
нет экстремума.
3) Если 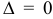 , то вопрос о наличии или отсутствии экстремума функции остается открытым (требуется дальнейшее исследование функции, например, по знаку приращения
, то вопрос о наличии или отсутствии экстремума функции остается открытым (требуется дальнейшее исследование функции, например, по знаку приращения 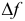 вблизи этой точки).
вблизи этой точки).
Пример №1
Найти экстремум функции 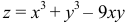 .
.
Решение:
1) Находим частные производные первого порядка
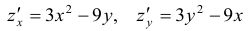
2) Воспользовавшись необходимыми условиями, находим стационарные точки
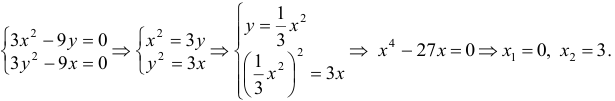
Из первого уравнения системы получим 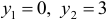 . Таким образом, найдены две стационарные точки
. Таким образом, найдены две стационарные точки 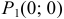 и
и 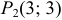 .
.
3) Находим частные производные второго порядка и их значения в стационарных точках: 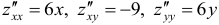 .
.
В точке 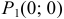
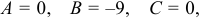
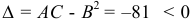 и в точке
и в точке 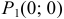 нет экстремума.
нет экстремума.
В точке 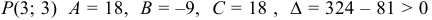 ,
, 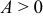 и в точке
и в точке 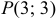 функция имеет минимум. Величина этого минимума
функция имеет минимум. Величина этого минимума 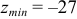 .
.
Пример №2
Исследовать функцию 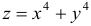 на экстремум.
на экстремум.
Решение:
Здесь стационарной точкой является (0; 0). В этой точке 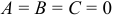 и поэтому
и поэтому 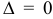 , т. е. теорема не применима. Но поскольку в точке (0; 0) будет
, т. е. теорема не применима. Но поскольку в точке (0; 0) будет 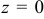 , а во всех остальных точках
, а во всех остальных точках 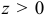 , то ясно, что здесь мы имеем минимум. Разумеется, что не всегда дело обстоит так просто.
, то ясно, что здесь мы имеем минимум. Разумеется, что не всегда дело обстоит так просто.
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Производные и дифференциалы высших порядков |
| Касательная плоскость и нормаль к поверхности |
| Условный экстремум |
| Производная в данном направлении. Градиент функции |

