Оглавление:
Касательной плоскостью к поверхности в данной точке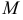 
(точке касания) называется плоскость, в которой лежат касательные в этой точке к всевозможным кривым, проведенным на данной поверхности через указанную точку.
Нормалью к поверхности называется перпендикуляр к касательной плоскости в точке касания.
Для поверхности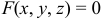 
уравнения касательной плоскости и нормали в точке 
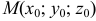имеют вид:
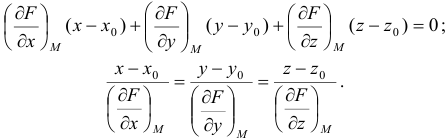
Для поверхности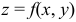 
уравнения касательной плоскости и нормали в точке 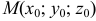принимают вид:
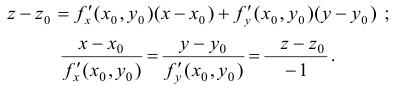
Пример №1
Составить уравнение касательной плоскости и нормали к поверхности:
а)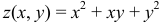 
в точке 
,
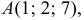б)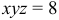 
в точке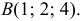 
Решение:
а) Для составления уравнений касательной плоскости и нормали к поверхности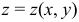 
в точке 
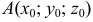используем формулы:
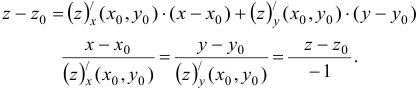
Из условия имеем: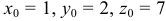 
, точка 
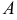принадлежит данной поверхности.
Подставляя значения частных производных и координат т. 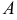в уравнения, получим
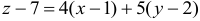— уравнение касательной плоскости.
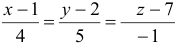— уравнение нормали.
б) Для поверхности, заданной уравнением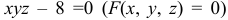 
используем формулы:
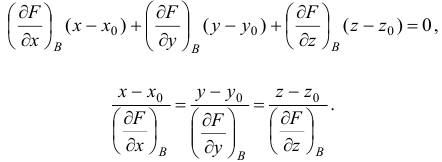
В нашем случае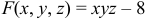 
,
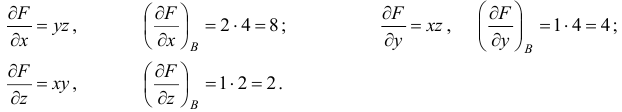
Уравнение касательной плоскости имеет вид: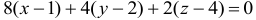 
или 
.
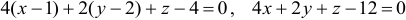Уравнение норма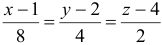ли:
или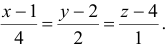 
Пример №2
Определить плоскость, касательную к поверхности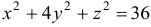 
и параллельной плоскости 
.
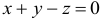Решение:
Уравнение искомой плоскости имеет вид
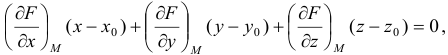
где 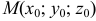— точка касания,
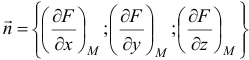— нормальный вектор.
По условию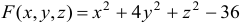 
. Следовательно,
Так как искомая плоскость параллельна данной плоскости 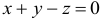с нормальным вектором 
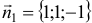, параллельным вектору 
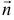, то их координаты будут пропорциональны 
.
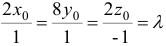Поскольку точка 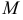принадлежит поверхности, то ее координаты можно вычислить, решив систему:
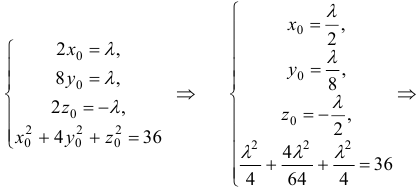
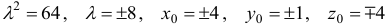. Имеем две точки касания 
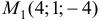и 
.
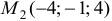Для точки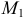 
уравнение касательной плоскости имеет вид
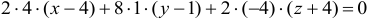или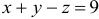 
.
Для точки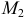 
уравнение касательной плоскости имеет вид
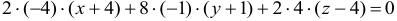или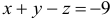 
.
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Частные производные и полный дифференциал функции |
| Производные и дифференциалы высших порядков |
| Экстремум функции нескольких переменных |
| Условный экстремум |
