Рассмотрим функцию трех переменных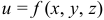 
. Без указания направления движения точки 
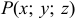нельзя говорить о скорости изменения функции (иначе, о производной функции в этой точке). Но производная по любому направлению есть линейная комбинация частных производных (производных по направлениям, параллельным осям координат). В направлении, параллельном оси 
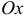, остаются постоянными другие аргументы и функция 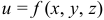становится функцией одного переменного 
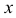. Частная производная
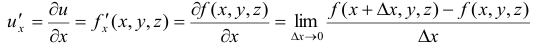
есть предел отношения частного приращения
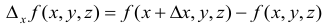
функции к приращению соответствующего аргумента, когда приращение аргумента стремится к нулю. Так же определяются для функции трех переменных две другие частные производные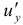 
и 
.
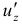Механический смысл частных производных ясен. Они указывают быстроту изменения функции 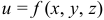в точке 
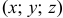по направлениям, параллельным осям координат.
Нетрудно понять и геометрический смысл частной производной. При постоянных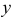 
и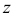 
уравнению 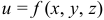отвечает кривая и 
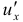— угловой коэффициент ее касательной в точке 
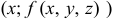. Аналогичный смысл имеют и другие частные производные.
Все правила и формулы дифференцирования, выведенные для функций одной переменной, полностью сохраняются при нахождении частных производных нескольких переменных. Важно только помнить, что при нахождении, например, производной по 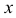с остальными аргументами обращаются как с постоянными величинами.
Существование частных производных в окрестности точки и непрерывность в точке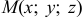 
обеспечивает дифференцируемость функции в этой точке. Выражение 
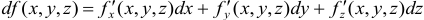называется полным дифференциалом дифференцируемой функции .
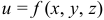Пример №1
Найти частные производные первого порядка функции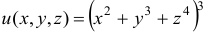 
.
Решение:
Для заданной функции существуют три частные производные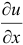 
, 
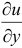и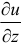 
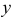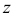. Считая и постоянными и дифференцируя 
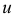как функцию от 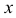, получим частную производную по переменной : 
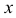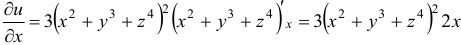, т.е. 
.
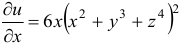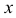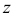Аналогично, считая и постоянными и дифференцируя 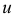как функцию от 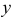, получим частную производную по переменной :
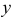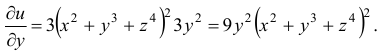
И, наконец,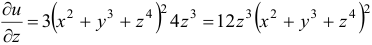 
.
Пример №2
Найти частные производные первого порядка функции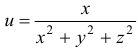 
по переменным 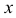и .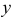
Решение:
Пользуясь правилами нахождения частных производных, получим:
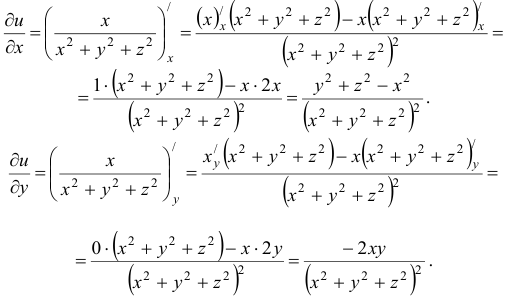
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Действия с комплексными числами, заданными в тригонометрической форме |
| Функций многих переменных |
| Производные и дифференциалы высших порядков |
| Касательная плоскость и нормаль к поверхности |
