Пусть даны два комплексных числа: 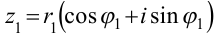 и
и 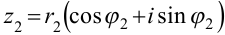 .
.
Теорема 1. Модуль произведения двух комплексных чисел равен произведению их модулей, а аргумент — сумме их аргументов.
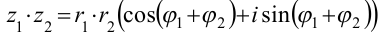
Теорема справедлива для любого числа сомножителей, т. е. при любом 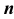 .
.
В частном случае, когда все сомножители равны между собой, получаем формулу Муавра:
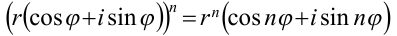
Теорема 2. Модуль частного двух комплексных чисел равен частному модулей делимого и делителя, а аргумент — разности аргументов делимого и делителя.
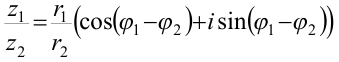
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Решение алгебраических уравнений в поле комплексных чисел |
| Тригонометрическая форма комплексных чисел |
| Функций многих переменных |
| Частные производные и полный дифференциал функции |
