Множество всех действительных чисел находится во взаимно однозначном соответствии с множеством всех точек числовой прямой.
Множество всех комплексных чисел находится во взаимном однозначном соответствии с множеством всех точек плоскости. То есть, каждому комплексному числу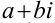 
соответствует одна определенная точка на плоскости с координатами 
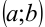и наоборот.
С каждой точкой плоскости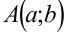 
можно связать вектор 
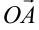, выходящий из начала координат и оканчивающийся в точке 
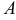. Координаты вектора 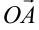при этом будут такими же, как и координаты точки 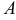. Очевидно, множество всех комплексных чисел находится во взаимном однозначном соответствии с множеством всех векторов плоскости, выходящих из начала координат.
Пусть комплексному числу 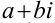соответствует вектор 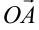с
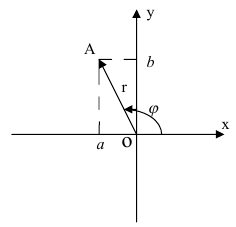
координатами 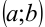(см рис 32). Обозначим длину вектора 
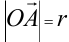, а угол, который он образует с осью 
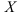, через 
.
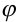По определению синуса и косинуса: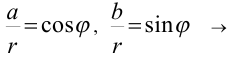 
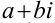. Комплексное число можно записать в виде: 
.
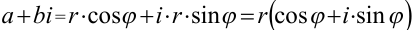Итак, любое комплексное число 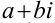можно представить в тригонометрической форме: 
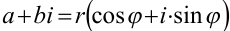, где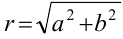 
, а угол определяется из условия:
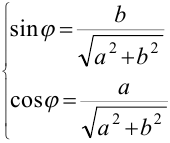или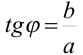 
.
Число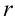 
называется модулем 
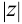, а угол 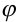— аргументом 
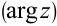комплексного числа 
.
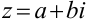На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
