Понятие числа прошло длинный путь исторического развития.
Одним из простейших числовых множеств является множество натуральных чисел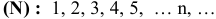 
В нем всегда выполнимы два основных (прямых) алгебраических действия: сложение и умножение. Это означает, что, каковы бы ни были натуральные числа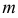 
и 
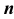, сумма их 
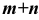, а также произведение 
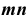являются непременно натуральными числами.
При этом соблюдаются следующие пять законов:
1) коммутативный ( переместительный) закон сложения:
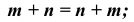
2) ассоциативный (сочетательный) закон сложения:
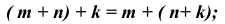
3) коммутативный ( переместительный) закон умножения:
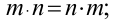
4) ассоциативный (сочетательный) закон умножения:
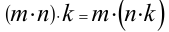
5) дистрибутивный ( распределительный) закон умножения относительно сложения:
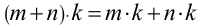
Вычитание и деление в множестве натуральных чисел выполнимы не всегда.
Чтобы действие вычитания было выполнимым всегда, множество натуральных чисел нужно расширить путем присоединения к нему всех отрицательных целых чисел и нуля. В результате мы получим множество всех целых чисел (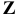
):
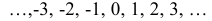
Числовое множество, в котором всегда выполнимы сложение и умножение, подчиненные указанным выше пяти законам, а также вычитание, называется кольцом.
Таким образом, множество 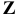образует кольцо . Чтобы действие деления было всегда выполнимым , множество целых чисел расширили путем присоединения к нему всех обыкновенных дробей, то есть чисел вида 
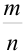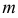, где и 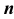— произвольные целые числа и 
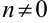. В результате такого расширения мы получаем множество всех рациональных чисел. Любую обыкновенную дробь можно представить в виде бесконечной периодической дроби, поэтому рациональные числа — это числа, представимые в виде бесконечных периодических десятичных дробей.
Множество чисел, в котором всегда выполнимы действия сложения и умножения, подчиненные пяти основным законам, а также действия вычитания и деления ( кроме деления на нуль), называется полем.
Множество рациональных чисел является простейшим числовым полем.
Числа, которые можно представить, в виде бесконечных непериодических десятичных дробей, называются иррациональными ( т. е. нерациональными).
Все рациональные и все иррациональные числа, взятые вместе, образуют множество действительных чисел (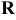 
).
Множество 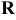образует поле. Заметьте, что множество иррациональных чисел поля не образует. Так, например, 
.
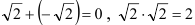На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
