Системой дифференциальных уравнений называется совокупность уравнений, в каждое из которых входит независимая переменная, искомые функции и их производные.
Решение системы, состоящей из нескольких уравнений с таким же числом неизвестных функций, можно привести к решению дифференциального уравнения с одной неизвестной функцией.
Нормальная система уравнений:
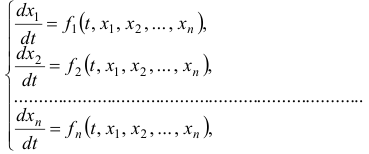
как правило, может быть заменена одним дифференциальным уравнением, порядок которого равен порядку системы.
Пример:
Найти общее решение системы уравнений
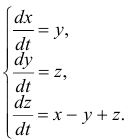
Решение:
Продифференцировав первое уравнение по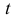 
, заменим производную 
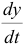ее выражением из второго уравнения: 
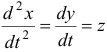. Продифференцировав полученное уравнение еще раз, заменим производную 
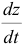ее выражением из третьего уравнения: 
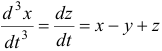. Подставляя в последнее уравнение 
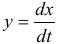и 
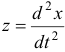, окончательно получим 
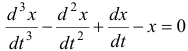. Решим это уравнение. Соответствующее ему характеристическое уравнение 
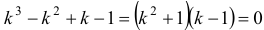имеет корни 
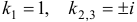. Следовательно, 
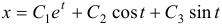. Функци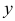и 
и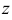 
в соответствии с соотношениям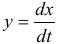и и 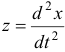после дифференцирования полученного для 
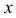выражения имеют вид: 
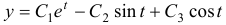и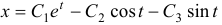 
.
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
