Оглавление:
Рассмотрим сначала понятие однородной функции двух переменных.
Функция двух переменных 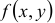 называется однородной функцией измерения
называется однородной функцией измерения 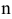 ,если при любом
,если при любом 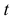 справедливо тождество
справедливо тождество 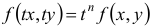 .
.
Пример:
Функция 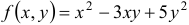 есть однородная функция второго измерения, т.к.
есть однородная функция второго измерения, т.к.
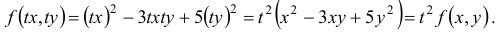
С понятием однородной функции связано понятие однородного дифференциального уравнения.
Уравнение 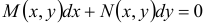 называется однородным дифференциальным уравнением первого порядка, если функции
называется однородным дифференциальным уравнением первого порядка, если функции 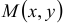 и
и 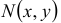 являются однородными функциями одного и того же измерения.
являются однородными функциями одного и того же измерения.
Однородные дифференциальные уравнения решаются введением новой переменной 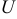 по формуле
по формуле 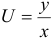 или
или 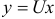 , при этом
, при этом 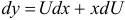 .
.
После подстановки данное однородное уравнение будет являться уравнением с разделяющимися переменными 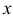 и
и 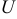 ; из него определяется
; из него определяется 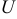 , а из формулы
, а из формулы 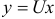 искомая функция
искомая функция 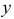 .
.
Пример:
Решить уравнение 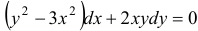 , если
, если 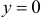 при
при 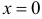 .
.
Решение:
Здесь 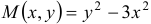 и
и 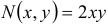 — однородные функции второго измерения. Применим подстановку
— однородные функции второго измерения. Применим подстановку 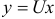 , при этом
, при этом 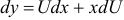 . Получим:
. Получим: 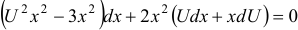 , или
, или 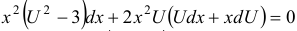 . Сгруппируем слагаемые относительно
. Сгруппируем слагаемые относительно 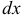 и
и 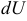 :
: 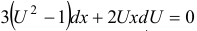 . Разделим переменные:
. Разделим переменные:
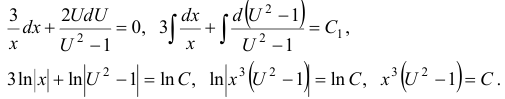
Так как 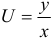 , то
, то 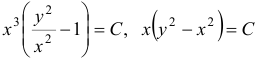 — общий интеграл. Используя начальные условия
— общий интеграл. Используя начальные условия 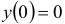 имеем
имеем 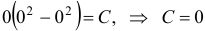 . Тогда
. Тогда 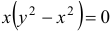 и
и 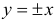 — частное решение данного уравнения.
— частное решение данного уравнения.
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Дифференциальные уравнения первого порядка: основные понятия |
| Уравнения с разделяющимися переменными |
| Линейные уравнения первого порядка |
| Уравнение Бернулли |

