Если дифференциальное уравнение первого порядка можно привести к виду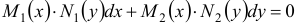 
, где множители 
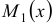и 
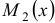зависят только от переменной 
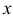, а множител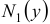и 
и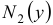 
зависят только от переменной 
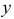, то оно называется уравнением с разделяющимися переменными.
Это уравнение решается путем деления обеих его частей на выражение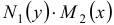 
:
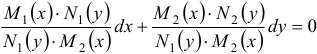или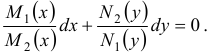 
Общий интеграл полученного уравнения имеет вид
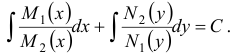
Пример:
Найти общий интеграл дифференциального уравнения
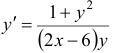или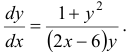 
Решение:
Разделим переменные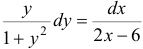 
и интегрируем 
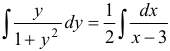. В результате вычисления интегралов получим: 
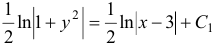. Это выражение можно записать в иной форме: 
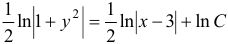, т.к. всякое число можно представить в виде логарифма другого.
Таким образом, общий интеграл данного уравнения будет иметь вид
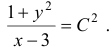
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Определенный интеграл |
| Дифференциальные уравнения первого порядка: основные понятия |
| Однородные уравнения первого порядка |
| Линейные уравнения первого порядка |
