Оглавление:
Общая схема исследования функции и построения ее графика:
- Найти область определения функции (
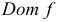 ). Исследовать поведение
). Исследовать поведение 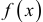 в граничных точках
в граничных точках 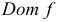 .
. - Установить, не является ли
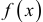 четной (или нечетной).
четной (или нечетной). - Является ли
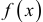 периодической?
периодической? - Исследовать
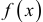 на непрерывность. Найти точки разрыва и установить их характер. Указать вертикальные асимптоты.
на непрерывность. Найти точки разрыва и установить их характер. Указать вертикальные асимптоты. - Найти уравнения наклонных асимптот.
- Найти нули
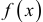 , т.е.
, т.е. 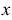 :
: 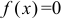 , и
, и 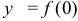 . Найти интервалы знакопостоянства.
. Найти интервалы знакопостоянства. - Вычислить
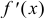 . Исследовать
. Исследовать 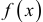 на монотонность и экстремумы.
на монотонность и экстремумы. - Вычислить
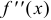 . Найти промежутки выпуклости и точки перегиба.
. Найти промежутки выпуклости и точки перегиба. - Свести результаты в таблицу, добавить значения функции в характерных точках (экстремума, перегиба и т.д.) и построить эскиз графика
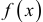 .
.
К числу характерных точек графика относятся точки пересечения его с осями координат. В случае непрерывной функции 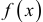 для нахождения абсцисс точек пересечения графика с осью
для нахождения абсцисс точек пересечения графика с осью 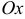 нужно найти корни уравнения
нужно найти корни уравнения 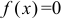 , лежащие в области существования графика. Удаляя из этой области найденные точки, получим разбиение области определения функции на интервалы знакопостоянства.
, лежащие в области существования графика. Удаляя из этой области найденные точки, получим разбиение области определения функции на интервалы знакопостоянства.
Из теоремы Ферма следует, что в точках локального экстремума непрерывной функции 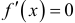 , если производная существует. Точки, удовлетворяющие этому условию, называются критическими точками функции
, если производная существует. Точки, удовлетворяющие этому условию, называются критическими точками функции 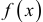 . Достаточные условия локального экстремума в критической точке
. Достаточные условия локального экстремума в критической точке 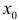 заключаются в смене знака
заключаются в смене знака 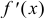 при переходе через эту точку из левой ее полуокрестности в правую. При этом смена знака с (+) на (-) отвечает максимуму, а смена знака с (-) на (+) — минимуму. Другой достаточный признак экстремума связан со знаком второй производной в критической точке. Если дважды дифференцируемая функция такова, что
при переходе через эту точку из левой ее полуокрестности в правую. При этом смена знака с (+) на (-) отвечает максимуму, а смена знака с (-) на (+) — минимуму. Другой достаточный признак экстремума связан со знаком второй производной в критической точке. Если дважды дифференцируемая функция такова, что 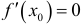 ,
, 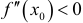 , то
, то 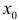 — точка локального максимума. Если же
— точка локального максимума. Если же 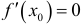 ,
, 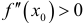 , то
, то 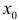 — точка локального минимума. На практике для нахождения интервалов монотонности нужно удалить из области определения функции все точки локального экстремума. Оставшееся множество состоит из интервалов монотонности. О возрастании и убывании функции на этих интервалах можно судить по знаку
— точка локального минимума. На практике для нахождения интервалов монотонности нужно удалить из области определения функции все точки локального экстремума. Оставшееся множество состоит из интервалов монотонности. О возрастании и убывании функции на этих интервалах можно судить по знаку 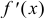 .
.
Дуга графика на интервале 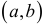 называется выпуклой вверх, если она расположена под каждой касательной к ней. Достаточным условием выпуклости вверх является
называется выпуклой вверх, если она расположена под каждой касательной к ней. Достаточным условием выпуклости вверх является 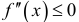 для всех
для всех 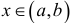 . Аналогично, дуга графика на интервале
. Аналогично, дуга графика на интервале 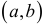 называется выпуклой вниз, если она расположена над каждой касательной к ней. Достаточным условием выпуклости вниз является
называется выпуклой вниз, если она расположена над каждой касательной к ней. Достаточным условием выпуклости вниз является 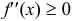 для всех
для всех 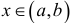 .
.
Точки перегиба на графике дифференцируемой функции обладают свойством: по обе стороны от них график имеет разное направление выпуклости. Достаточным условием перегиба является существование 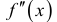 в окрестности точки
в окрестности точки 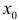 и смена знака
и смена знака 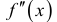 при переходе через точку
при переходе через точку 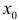 . При этом
. При этом 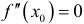 .
.
Вертикальные асимптоты к графику функции 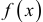 — это прямые вида
— это прямые вида 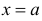 , такие, что хотя бы один из односторонних пределов этой функции при
, такие, что хотя бы один из односторонних пределов этой функции при 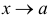 равен бесконечности. Это может иметь место в точках разрыва второго рода либо в граничных точках области определения функции. Наклонная асимптота при
равен бесконечности. Это может иметь место в точках разрыва второго рода либо в граничных точках области определения функции. Наклонная асимптота при 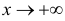 — это прямая
— это прямая 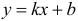 , где
, где 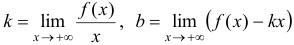 . Аналогично определяется наклонная асимптота при
. Аналогично определяется наклонная асимптота при 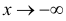 . Наклонные асимптоты возможны только в случае, когда область определения функции не ограничена.
. Наклонные асимптоты возможны только в случае, когда область определения функции не ограничена.
Пример 1.
Исследовать методами дифференциального исчисления функцию 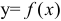 и, используя результаты исследования, построить ее график: а)
и, используя результаты исследования, построить ее график: а) 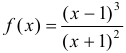 , б)
, б) 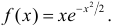
Решение:
а) 1. Очевидно, что 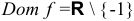 .
.
2. 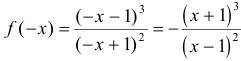 . Заметим, что
. Заметим, что 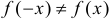 и
и 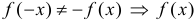 не является ни четной, ни нечетной.
не является ни четной, ни нечетной.
3. Функция 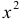 не является периодической , поскольку
не является периодической , поскольку 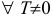
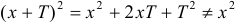 .
.
Аналогично убеждаемся в том, что 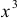 не является периодической функцией. Следовательно,
не является периодической функцией. Следовательно, 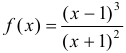 не является периодической функцией.
не является периодической функцией.
4. 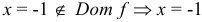 — точка разрыва. Найдем
— точка разрыва. Найдем 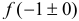 .
.
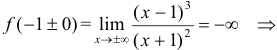 прямая
прямая 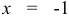 является вертикальной асимптотой.
является вертикальной асимптотой.
5. Найдем уравнения наклонных асимптот. Вычисления дают:
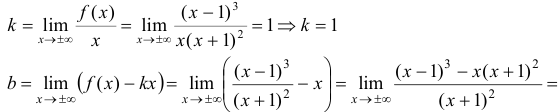
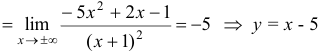 — наклонная асимптота при
— наклонная асимптота при 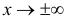 .
.
6. Заметим, что 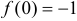 и
и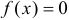 при
при 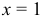 .
.
7. Находим: 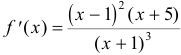 . Тогда, исследуя знаки
. Тогда, исследуя знаки  методом интервалов, заключаем, что
методом интервалов, заключаем, что  возрастает на
возрастает на 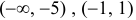 и
и 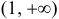 и убывает на
и убывает на 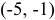 . Таким образом, в точке
. Таким образом, в точке 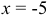
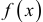 имеет экстремум:
имеет экстремум: 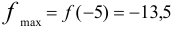 . В точке
. В точке 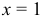 экстремума нет (почему мы не рассматриваем точку
экстремума нет (почему мы не рассматриваем точку 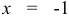 ?). Однако указанные особенности поведения функции еще не позволяют нам однозначно судить о виде графика
?). Однако указанные особенности поведения функции еще не позволяют нам однозначно судить о виде графика 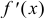 . Очевидно, что окончательный ответ на этот вопрос мы можем получить, только исследовав промежутки выпуклости
. Очевидно, что окончательный ответ на этот вопрос мы можем получить, только исследовав промежутки выпуклости 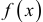 .
.
8. Находим: 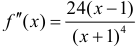 . Точка возможного перегиба —
. Точка возможного перегиба — 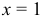 , интервалы выпуклости —
, интервалы выпуклости — 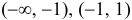 и
и 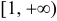 . Установим знаки
. Установим знаки 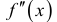 на каждом из этих интервалов. Заключаем, что
на каждом из этих интервалов. Заключаем, что 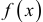 выпукла вверх на
выпукла вверх на 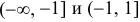 и выпукла вниз на
и выпукла вниз на 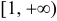 . Точка
. Точка 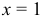 является точкой перегиба.
является точкой перегиба.
9. Сведем полученные данные в таблицу 1. Добавим значение 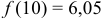 .
.
Таблица 1
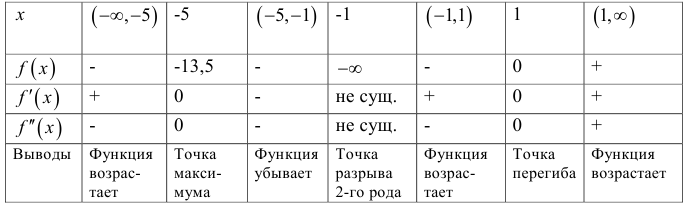
Эскиз графика 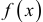 представлен на (рис. 19).
представлен на (рис. 19).
б) 1. Функция определена и непрерывна на 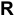 .
.
2. Функция нечетная: 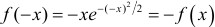 . Следовательно, ее график симметричен относительно начала координат.
. Следовательно, ее график симметричен относительно начала координат.
3. Не периодическая.
4. Точек разрыва нет, следовательно, нет вертикальных асимптот.
5. Ищем наклонные асимптоты:
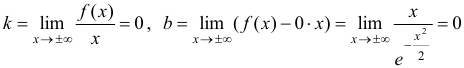
(предел находится по правилу Лопиталя). Итак, наклонная асимптота имеет уравнение 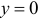 .
.
6. Очевидно, 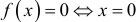 . График проходит через начало координат и других общих точек с осями координат не имеет. На
. График проходит через начало координат и других общих точек с осями координат не имеет. На 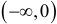 имеем
имеем 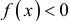 , следовательно, график расположен ниже оси абсцисс. На
, следовательно, график расположен ниже оси абсцисс. На 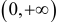 имеем
имеем 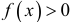 , следовательно, график расположен выше оси абсцисс.
, следовательно, график расположен выше оси абсцисс.
7. Исследуем функцию с помощью 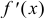 . Имеем
. Имеем 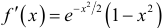 .
. 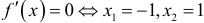 — критические точки. На
— критические точки. На 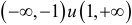 функция убывает, так как
функция убывает, так как 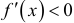 . На (-1,1) функция возрастает, так как
. На (-1,1) функция возрастает, так как 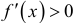 . Следовательно,
. Следовательно, 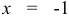 — точка минимума,
— точка минимума, 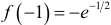 ;
; 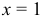 — точка максимума,
— точка максимума, 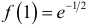 .
.
8. Исследуем функцию с помощью 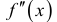 . Имеем
. Имеем 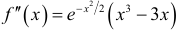 . Отсюда
. Отсюда 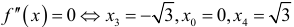 — точки возможного перегиба. На
— точки возможного перегиба. На 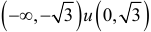
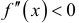 — график выпуклый вверх. На интервалах
— график выпуклый вверх. На интервалах 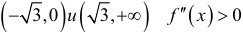 — график выпуклый вниз. Точки перегиба
— график выпуклый вниз. Точки перегиба 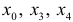 . Значения функции в этих точках
. Значения функции в этих точках 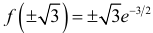 ,
, 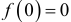 .
.
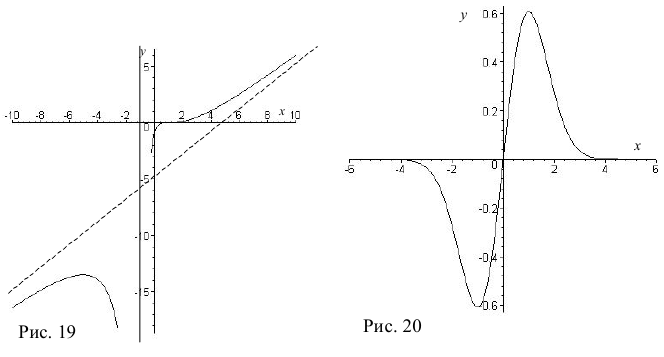
9. Сводим результаты исследования в таблицу 2, пользуясь нечетностью функции, и строим эскиз графика (рис. 20).
Таблица 2

Пример 2.
Дан прямой круговой конус 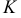 с радиусом основания
с радиусом основания 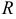 , образующая его наклонена к плоскости основания под углом
, образующая его наклонена к плоскости основания под углом 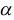 . Требуется вписать в
. Требуется вписать в 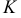 прямой круговой конус
прямой круговой конус 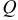 наибольшего объема при условии, что вершина
наибольшего объема при условии, что вершина 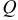 совпадает с центром основания конуса
совпадает с центром основания конуса 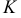 .
.
Решение:
Сделаем чертеж (рис. 21). Рассмотрим осевое сечение конуса 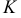 . Пусть
. Пусть 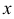 — радиус основания вписанного конуса. Его высота
— радиус основания вписанного конуса. Его высота 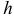 находится из прямоугольного треугольника
находится из прямоугольного треугольника 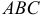 . Так как
. Так как 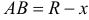 , то
, то 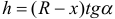 . Итак, объем вписанного конуса
. Итак, объем вписанного конуса 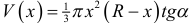 . Найдем максимум этой функции на промежутке
. Найдем максимум этой функции на промежутке 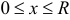 . Производная
. Производная 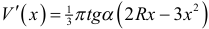 . Отсюда
. Отсюда 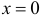 или
или 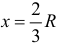 . При
. При 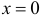 объем конуса
объем конуса 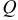 равен нулю. При переходе через вторую критическую точку производная
равен нулю. При переходе через вторую критическую точку производная 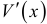 меняет знак с плюса на минус. Значит, объем конуса будет максимальным при
меняет знак с плюса на минус. Значит, объем конуса будет максимальным при 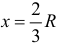 .
.
Ответ: 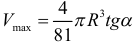 . Объем конуса
. Объем конуса 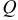 составляет
составляет 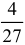 объема конуса
объема конуса 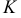 .
.
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:

