Оглавление:
Если дифференцируемая функция 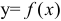 удовлетворяет уравнению
удовлетворяет уравнению 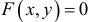 , то производная
, то производная 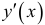 этой неявной функции может быть найдена из уравнения
этой неявной функции может быть найдена из уравнения 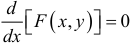 , где
, где 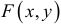 рассматривается как сложная функция переменной
рассматривается как сложная функция переменной 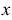 .
.
Пример 1.
Найти производные 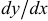 данных функций:
данных функций:
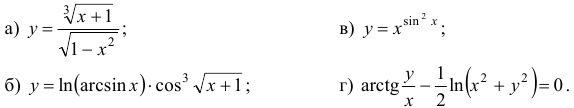
Решение:
а) Комбинируя правила нахождения производных сложной функции и частного, получим
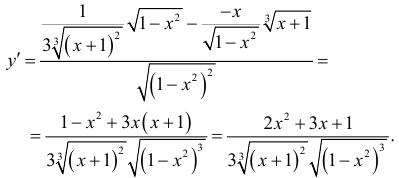
б) Комбинируя правила нахождения производных сложной функции и произведения функций, будем иметь
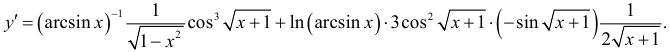
в) Запишем данную функцию в виде 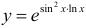 и применим правило дифференцирования сложной функции:
и применим правило дифференцирования сложной функции:
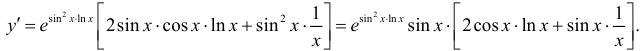
г) Продифференцируем обе части тождества по 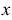 , считая
, считая 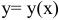 .
.
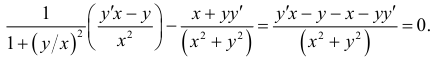
Следовательно, числитель последней дроби равен нулю: 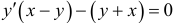 . В итоге получаем
. В итоге получаем 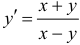 .
.
Пример 2.
Найти 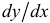 и
и 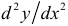 для заданных функций:
для заданных функций:

Решение:
а) 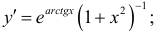
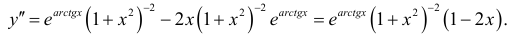
б) Применим правила нахождения производных от функции, заданной параметрически 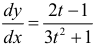 . Так как
. Так как 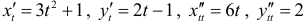 , то
, то
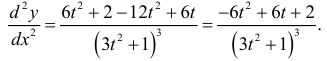
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:

