Оглавление:
Если вектор 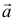 векторно умножается на вектор
векторно умножается на вектор 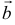 , а затем получившийся при этом вектор
, а затем получившийся при этом вектор 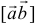 скалярно умножается на вектор
скалярно умножается на вектор 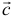 , то в результате получается число
, то в результате получается число 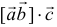 , называемое смешанным произведением векторов
, называемое смешанным произведением векторов 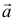 ,
, 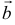 и
и 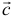 .
.
Геометрическое свойство смешанного произведения
Смешанное произведение 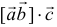 равно объему параллелепипеда, построенного на приведенных к общему началу векторах
равно объему параллелепипеда, построенного на приведенных к общему началу векторах 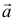 и
и 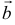 , взятому со знаком плюс, если тройка
, взятому со знаком плюс, если тройка 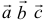 правая, и со знаком минус, если тройка
правая, и со знаком минус, если тройка 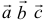 левая.
левая.
Свойства смешанного произведения
1) знаки операций «крест» и «точка» можно менять местами:
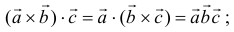
2) необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения;
3) смешанное произведение трех векторов, два из которых совпадают, равно нулю;
4) от перестановки двух сомножителей смешанное произведение меняет знак:
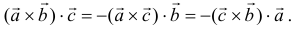
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Сферическая система координат |
| Векторное произведение векторов |
| Векторное и смешанное произведения в декартовых координатах |
| Алгебраические линии и поверхности |

