Три вектора называются упорядоченной тройкой (или просто тройкой), если указано, какой из этих векторов является первым, какой — вторым и какой — третьим.
Тройка некомпланарных векторов 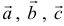 называется правой (левой), если выполнено условие: находясь внутри телесного угла, образованного приведением к общему началу векторами
называется правой (левой), если выполнено условие: находясь внутри телесного угла, образованного приведением к общему началу векторами 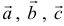 , мы видим поворот от
, мы видим поворот от 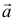 к
к 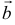 и от него к
и от него к 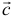 , совершающийся против часовой стрелки (по часовой стрелки).
, совершающийся против часовой стрелки (по часовой стрелки).
Декартова система координат называется правой (левой), если три базисных вектора образуют правую (левую) тройку.
В дальнейшем мы будем рассматривать только правые системы координат.
Векторным произведением вектора 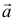 на вектор
на вектор 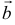 называется вектор
называется вектор 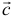 , обозначаемый
, обозначаемый 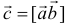 или
или 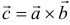 и отвечающий следующими требованиям:
и отвечающий следующими требованиям:
- длина вектора
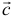 равна произведению длин векторов
равна произведению длин векторов 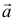 и
и 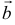 на синус угла
на синус угла 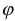 между ними:
между ними: 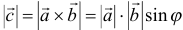 , причем
, причем 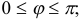
- вектор с ортогонален к каждому из векторов
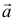 и
и 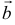 ;
; - вектор с направлен так, что тройка векторов
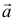 ,
, 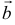 и
и 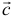 является правой.
является правой.
Геометрические свойства векторного произведения
- Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения.
- Длина (модуль) векторного произведения
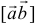 равняется площади параллелограмма, построенного на приведенных к общему началу векторах
равняется площади параллелограмма, построенного на приведенных к общему началу векторах 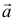 и
и 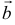 .
.
Алгебраические свойства векторного произведения:

На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Цилиндрическая система координат |
| Сферическая система координат |
| Смешанное произведение трех векторов |
| Векторное и смешанное произведения в декартовых координатах |

