Оглавление:
Определения
Систему уравнений вида
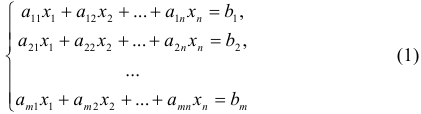
называют системой 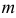 линейных уравнений с
линейных уравнений с 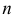 неизвестными.
неизвестными. 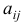 называют коэффициентами этих уравнений, которые записываются в виде матрицы (матрица системы):
называют коэффициентами этих уравнений, которые записываются в виде матрицы (матрица системы):
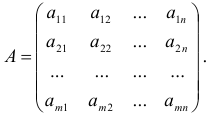
Числа, стоящие в правых частях уравнений, обозначают столбцом 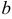 , называемым столбцом свободных членов.
, называемым столбцом свободных членов.
Матрица системы, дополненная справа столбцом свободных членов.
называется расширенной матрицей системы:
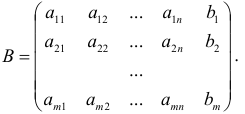
Нашу систему уравнений можно записать в матричной форме 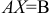 , где
, где 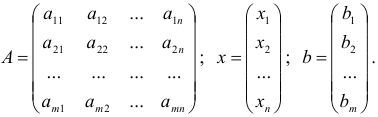
Если все свободные члены равны нулю, то систему называют однородной.
Совокупность 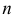 чисел (
чисел (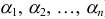 ) называется решением системы (1), если каждое ее уравнение обращается в числовое равенство после подстановки в него чисел
) называется решением системы (1), если каждое ее уравнение обращается в числовое равенство после подстановки в него чисел 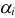 , вместо соответствующих неизвестных
, вместо соответствующих неизвестных 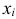 для всех
для всех 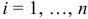 .
.
Система, имеющая хотя бы одно решение, называется совместной, а не имеющая — несовместной.
Решение называется тривиальным, если нулевой вектор 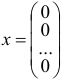 является решением системы.
является решением системы.
Решение систем 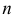 линейных уравнений с
линейных уравнений с 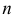 неизвестными с помощью формул Крамера.
неизвестными с помощью формул Крамера.
Для простоты рассмотрим систему трех линейных уравнений с тремя неизвестными: 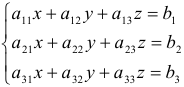
Определитель, составленный из коэффициентов при неизвестных, называется главным и обозначается символом  , т.е.
, т.е.
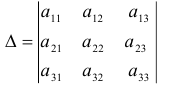
Вспомогательные определители системы для вычисления переменных 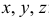 :
:
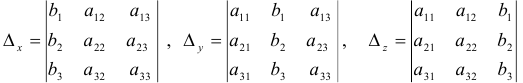
Нетрудно увидеть закономерность при составлении вспомогательных определителей!
Теорема Крамера
1) Если главный определитель системы не равен нулю, то система имеет единственное решение. Это решение находится по формулам 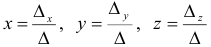 .
.
2) Если главный определитель системы равен нулю, а хотя бы один из вспомогательных определителей не равен нулю, то такая система не имеет решения (несовместна).
3) Если главный определитель системы равен нулю и все вспомогательные определители равны нулю т. е. 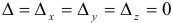 , то такая система имеет бесчисленное множество решений.
, то такая система имеет бесчисленное множество решений.
Пример 1.
Решить систему уравнений
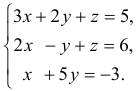
Решение:
По теореме Крамера имеем 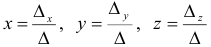 .
.
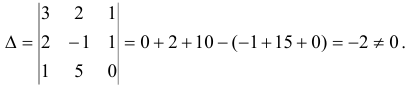
Определитель матрицы системы отличен от нуля. Следовательно, по теореме Крамера система имеет единственное решение. Найдем вспомогательные определители системы:
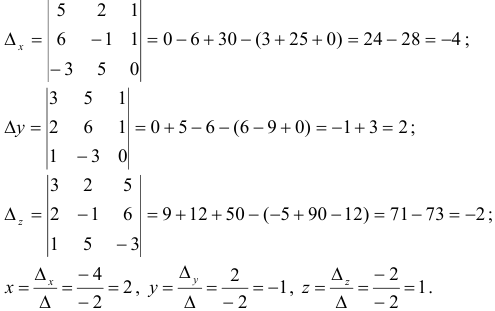
Ответ: 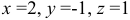 .
.
Если определитель  однородной системы не равен нулю (
однородной системы не равен нулю (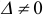 ), то эта система имеет только тривиальное решение.
), то эта система имеет только тривиальное решение.
Если однородная система уравнений имеет нетривиальное решение, то ее определитель  равен нулю.
равен нулю.
Решение двух однородных линейных уравнений с тремя неизвестными
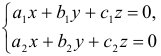
когда хотя бы один из миноров 2-го порядка отличен от нуля удобно искать по формулам:
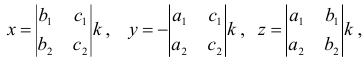
где 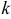 — произвольное число.
— произвольное число.
Теорема Кронекера — Капелли
Неоднородная система линейных уравнений совместна тогда, и только тогда, когда ранг матрицы системы 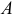 равен рангу расширенной матрицы системы
равен рангу расширенной матрицы системы 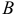 .
.
Следствие. Если ранг матрицы 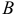 не равен рангу матрицы
не равен рангу матрицы 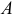 , то система не имеет решений (она несовместна).
, то система не имеет решений (она несовместна).
Пример 2.
Определить совместны ли системы:

Решение:
а) 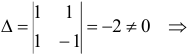 система совместна, т.к.
система совместна, т.к. 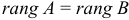 .
.
б) 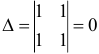 .
.
Найдем ранг матрицы. Вычитаем из второй строки первую, а потом вычеркиваем нулевую строку:
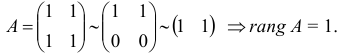
Найдем ранг расширенной матрицы. Вычитаем из второй строки первую, а потом переставляем 2-й и 3-й столбцы местами:
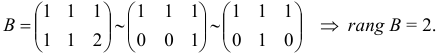
Так как 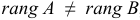 , то система несовместна.
, то система несовместна.
Ответ: а) система совместна, б) система несовместна.
Метод последовательных исключений Жордана — Гаусса
С помощью элементарных преобразований строк расширенная матрица системы приводится к треугольному виду. Обычно нули получают ниже главной диагонали.
При решении методом Жордана — Гаусса системы трех линейных уравнений с тремя неизвестными после приведения расширенной матрицы системы к треугольному виду получится:
а) 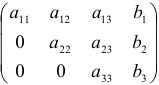 , где
, где 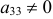 (система будет иметь единственное решение);
(система будет иметь единственное решение);
б) 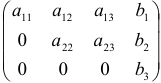 , где
, где 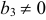 (система будет несовместной);
(система будет несовместной);
в) 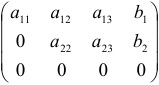 (система будет иметь множество решений).
(система будет иметь множество решений).
Задача:
Используя теорему Кронекера — Капелли, доказать совместность системы линейных уравнений и решить её двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления.
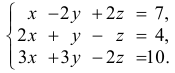
Решение:
Найдем ранг 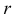 матрицы системы методом окаймляющих миноров.
матрицы системы методом окаймляющих миноров.
Рассмотрим минор 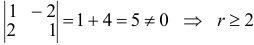 . Найдем определитель матрицы системы:
. Найдем определитель матрицы системы:
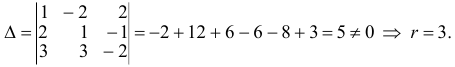
Ранг расширенной матрицы системы также равен трем, поскольку система содержит три уравнения, а ранг матрицы системы равен трем. Следовательно, согласно теореме Кронекера — Капелли, система совместна.
Первый способ решения (метод Гаусса):
Умножим первую строку на (-2) и результат прибавим ко второй, потом умножим первую строку на (-3) и результат прибавим к третьей:
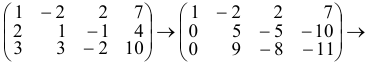
Разделим вторую строку на 5, потом умножим ее на (-9) и результат прибавили к третьей:
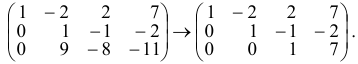
Из последней матрицы имеем 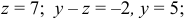
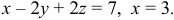
Второй способ решения:
Найдем алгебраические дополнения матрицы системы:
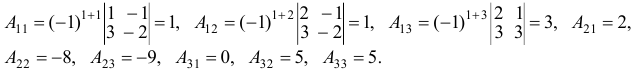
Запишем присоединенную матрицу и транспонируем ее:
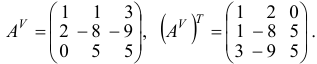
Решение системы:
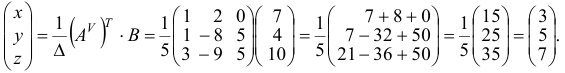
Ответ: 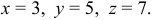
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Определители матрицы: алгоритм, примеры вычисления |
| Матрицы. Операции над матрицами |
| Векторная алгебра: основные понятия и определения |
| Проекция вектора на ось |

