Оглавление:
Ниже предлагается набор из нескольких задач преимущественно «транспортноэкономического» содержания. В каждой из них нужно найти минимум той или иной функции: времени передвижения, расходов на перевозку грузов и т. п. Иногда речь может идти о максимуме: например, о максимуме прибыли. Поэтому иногда подобные задачи мы будем называть также экстремальными.
Задача 1.
О кратчайшем пути для двух точек и прямой.
Дана прямая и две точки 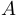 и
и 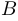 по одну сторону от нее. Где на прямой следует выбрать точку
по одну сторону от нее. Где на прямой следует выбрать точку 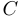 так, чтобы длина пути
так, чтобы длина пути 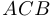 была бы наименьшей?
была бы наименьшей?
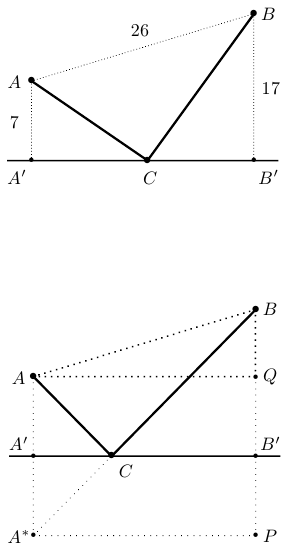
Чему равна длина этого пути, если расстояния от точек до прямой равны 7 км и 17 км, а расстояние между точками 26 км?
Решение:
Построим точку 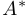 , симметричную точке
, симметричную точке 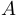 относительно заданной прямой. Путь из
относительно заданной прямой. Путь из 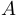 в
в 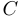 по длине совпадает с путем из
по длине совпадает с путем из 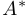 в
в 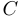 . В то же время самый короткий по длине путь из
. В то же время самый короткий по длине путь из 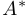 в
в 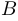 — это отрезок прямой, соединяющий
— это отрезок прямой, соединяющий 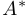 и
и 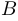 . Точка
. Точка 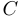 строится как точка пересечения отрезка
строится как точка пересечения отрезка 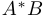 и заданной прямой.
и заданной прямой.
Для того чтобы вычислить длину пути 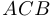 , заметим, что она равна длине отрезка
, заметим, что она равна длине отрезка 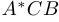 , то есть длине гипотенузы прямоугольного треугольника
, то есть длине гипотенузы прямоугольного треугольника 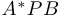 , где
, где 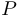 — основание перпендикуляра, опущенного из точки
— основание перпендикуляра, опущенного из точки 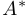 на вертикальную прямую
на вертикальную прямую 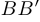 . Длина
. Длина 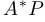 равна 24 (см. рисунок) и равна длине
равна 24 (см. рисунок) и равна длине 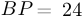 . Следовательно, искомая длина равна
. Следовательно, искомая длина равна 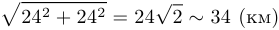 .
.
Задача 2.
О наиболее выгодном перемещении груза между двумя точками. Два пункта 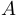 и
и 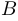 лежат по одну сторону от дороги
лежат по одну сторону от дороги 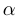 . Известно, что 1 км перевозки груза по дороге обходится в два раза дешевле, чем по любому другому пути вне дороги. Как следует двигаться, чтобы затраты на перевозку груза из
. Известно, что 1 км перевозки груза по дороге обходится в два раза дешевле, чем по любому другому пути вне дороги. Как следует двигаться, чтобы затраты на перевозку груза из 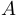 в
в 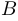 были бы наименьшими?
были бы наименьшими?
Чему равны эти затраты, если расстояние от пунктов 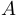 и
и 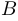 до дороги равны 60 км и 200 км, расстояние между точками
до дороги равны 60 км и 200 км, расстояние между точками 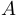 и
и 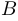 «напрямую» равно 500 км, а провоз груза на расстояние 1 км по дороге обходится в 10 экю?
«напрямую» равно 500 км, а провоз груза на расстояние 1 км по дороге обходится в 10 экю?
Какой будет траектория и какими будут затраты, если расстояние между 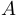 и
и 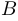 равно не 500, а 400 км?
равно не 500, а 400 км?
Решение:
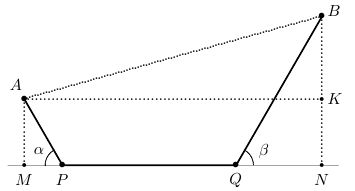
Опустим перпендикуляры 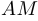 и
и 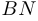 из точек
из точек 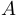 и
и 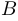 на прямую
на прямую 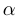 . По условию
. По условию 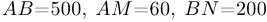 . Опустим перпендикуляр
. Опустим перпендикуляр 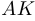 на
на 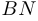 .
. 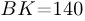 и по теореме Пифагора
и по теореме Пифагора 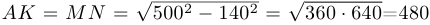 . Если движение производится по пути
. Если движение производится по пути 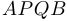 , то заметим, что точки
, то заметим, что точки 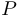 и
и 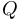 должны быть выбраны так, чтобы минимизировать стоимостную функцию
должны быть выбраны так, чтобы минимизировать стоимостную функцию 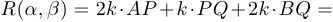
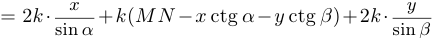 , где
, где 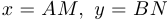 , а
, а 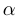 и
и 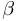 равны соответственно углам
равны соответственно углам 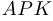 и
и 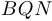 .
.
Представим 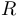 в виде
в виде
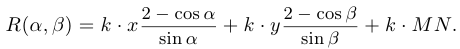
Поскольку величины 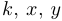 , и
, и 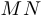 являются постоянными, то минимум функции
являются постоянными, то минимум функции 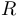 достигается при тех значениях углов
достигается при тех значениях углов 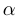 и
и 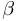 , при которых имеет минимум функция
, при которых имеет минимум функция
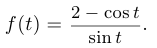
Подсчитаем производную этой функции.
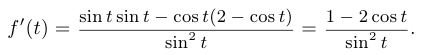
Таким образом,
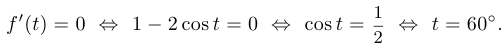
Поскольку минимум достигается в некоторой точке интервала (0, 90°), а критическое значение единственно, то оно и есть искомое. Таким образом, 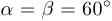 и поскольку
и поскольку 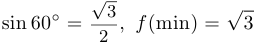 , то
, то
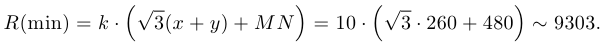
Поскольку расходы на перевозку по прямому пути 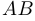 равны 10 000 экю, то этот путь менее выгоден. Следовательно, двигаться следует по пути
равны 10 000 экю, то этот путь менее выгоден. Следовательно, двигаться следует по пути 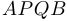 , где углы
, где углы 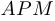 и
и 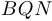 равны 60°.
равны 60°.
Отметим, что если 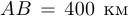 , то подсчет показывает, что движение по пути
, то подсчет показывает, что движение по пути 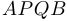 обходится приблизительно в 8250 экю, что означает, что движение по прямой
обходится приблизительно в 8250 экю, что означает, что движение по прямой 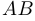 более выгодно.
более выгодно.
Задача 3.
О кратчайшем соединении для четырех точек. Четыре точки: 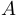 ,
, 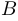 ,
, 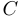 и
и 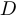 являются вершинами квадрата со стороной 1. Как следует соединить эти точки дорогами, чтобы было возможно проехать из любой точки в любую и чтобы сумма длин дорог была бы наименьшей? Какова при этом будет суммарная длина дорог?
являются вершинами квадрата со стороной 1. Как следует соединить эти точки дорогами, чтобы было возможно проехать из любой точки в любую и чтобы сумма длин дорог была бы наименьшей? Какова при этом будет суммарная длина дорог?
Решение:
Подсказка: На рисунке указаны несколько «допустимых» соединений, но среди них нет оптимального.

При разборе следующей задачи нам понадобится вспомогательное утверждение из элементарной геометрии, доказательство которого предлагается в качестве упражнения.
Лемма об окружности, описанной вокруг правильного треугольника. Сумма расстояний от произвольной точки на плоскости до двух ближайших вершин правильного треугольника всегда больше или равна расстоянию до третьей вершины, причем равенство достигается только для точек, лежащих на окружности, описанной вокруг этого треугольника.
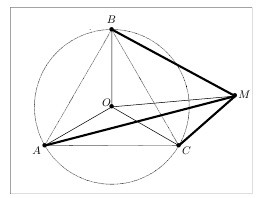
Упр. 1. 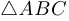 — правильный.
— правильный. 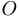 — центр описанной окружности.
— центр описанной окружности. 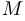 — произвольная точка на плоскости. Докажите, что
— произвольная точка на плоскости. Докажите, что 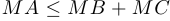 .
.
Упр. 2. 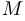 лежит на дуге
лежит на дуге 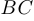 (меньшей) описанной окружности. Докажите, что
(меньшей) описанной окружности. Докажите, что 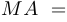
 .
.
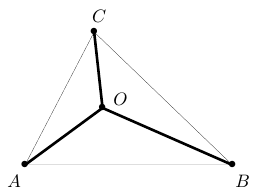
Задача 4.
Задача о точке Торричелли. Рассматривается произвольный треугольник 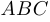 при предположении, что каждый из его углов меньше 120°. Найти такую точку на плоскости, для которой сумма расстояний до вершин треугольника является наименьшей.
при предположении, что каждый из его углов меньше 120°. Найти такую точку на плоскости, для которой сумма расстояний до вершин треугольника является наименьшей.
Решение:
Вне треугольника 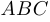 построим на каждой его стороне равносторонние треугольники и опишем вокруг них окружности. У этих окружностей единственная общая точка пересечения (докажите это!). Назовем ее
построим на каждой его стороне равносторонние треугольники и опишем вокруг них окружности. У этих окружностей единственная общая точка пересечения (докажите это!). Назовем ее 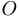 . Заметим, что
. Заметим, что 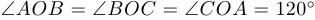 .
.
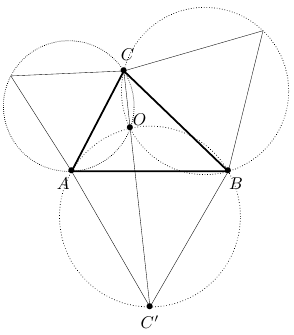
Покажем, что точка 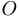 является искомой. Если искомая точка
является искомой. Если искомая точка 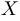 не совпадает с точкой
не совпадает с точкой 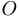 , то она находится вне одной из окружностей. Предположим, что это окружность, описанная вокруг треугольника
, то она находится вне одной из окружностей. Предположим, что это окружность, описанная вокруг треугольника 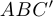 . Поскольку
. Поскольку 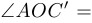
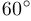 , а
, а 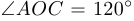 , то
, то 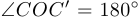 , то есть
, то есть 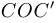 — прямая.
— прямая.
Далее в соответствии с леммой об окружности, описанной вокруг правильного треугольника, имеем, что 
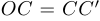 , в то время как
, в то время как 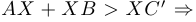
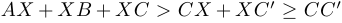 . Утверждение доказано.
. Утверждение доказано.
На этой странице найдёте другие готовые курсовые работы во высшей математике:
Много готовых курсовых работ по высшей математике
Можете посмотреть другие готовые курсовые работы по высшей математике:
| Курсовая работа на тему: решение уравнений большой степени |
| Курсовая работа на тему: выпуклые множества и функции |
| Курсовая работа на тему: Множества и операции с ними |
| Курсовая работа на тему: функции |

