Оглавление:
«Большой степенью» мы, в соответствии с традицией, называем степень больше двух. Если степень многочлена больше четырех, то мы будем называть ее «очень большой степенью». Задача этой лекции — рассказать о том, как решаются уравнения большой степени. Но перед этим мы должны сформулировать результат, который, несмотря на свою привычность, остается непростым. Основная теорема алгебры: Всякий отличный от константы многочлен с комплексными коэффициентами имеет хотя бы один комплексный корень. Следствие. Любой многочлен степени 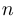 с комплексными коэффициентами имеет ровно
с комплексными коэффициентами имеет ровно 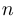 (комплексных) корней с учётом их кратности.
(комплексных) корней с учётом их кратности.
Более привычной является следующая формулировка основной теоремы.
Основная теорема алгебры: Всякий многочлен с вещественными коэффициентами можно разложить в произведение линейных и квадратичных множителей с вещественными коэффициентами.
Замечание 1. Если многочлен с вещественными коэффициентами имеет комплексный корень 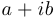 , то он имеет и комплексно-сопряженный корень
, то он имеет и комплексно-сопряженный корень 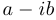 .
.
Замечание 2. Всякий многочлен с вещественными коэффициентами нечетной степени имеет хотя бы один вещественный корень.
Две следующие теоремы имеют непосредственное отношение к теме:
Теорема Безу. Если многочлен 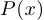 имеет корень
имеет корень 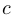 , то
, то  является его множителем (многочлен делится на
является его множителем (многочлен делится на  ).
).
Другими словами, если 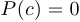 , то многочлен делится на
, то многочлен делится на  .
.
Следствие. Остаток от деления многочлена 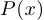 на
на  равен
равен 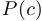 .
.
Теорема Виета. Если многочлен 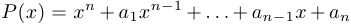 имеет корни
имеет корни 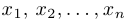 , (комплексные, каждый корень повторяется столько раз, какова его кратность), то
, (комплексные, каждый корень повторяется столько раз, какова его кратность), то
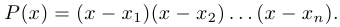
Следствие. (Формулы Виета). Справедливы равенства
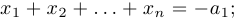
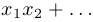 всевозможные попарные произведения
всевозможные попарные произведения 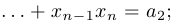
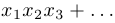 всевозможные произведения по три
всевозможные произведения по три 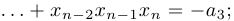
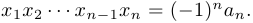
Замечание 3. Каждой паре комплексно-сопряженных корней 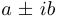 соответствует квадратичная функция
соответствует квадратичная функция 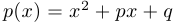 , где
, где 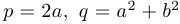 .
.
Пример 1.
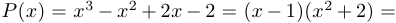
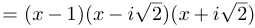 . Здесь
. Здесь 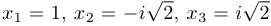 .
.
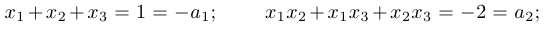
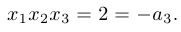
Пример 2.
Написать многочлен, корнями которого являются числа 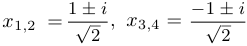 .
.
Решение:
Воспользовавшись замечанием 3, запишем две квадратичные функции: 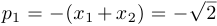 ,
, 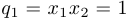 ;
; 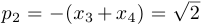 ,
, 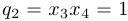 . Таким образом,
. Таким образом, 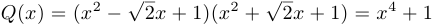 .
.
Ответ: 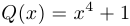 .
.
Решение кубических уравнений.
Кубическим уравнением общего вида называется уравнение 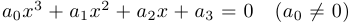 . Разделив обе части равенства на
. Разделив обе части равенства на 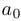 , получим
, получим
приведенное уравнение 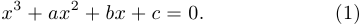
Нашей задачей является решение этого уравнения в вещественной области, то есть нахождение всех вещественных корней. На первых шагах мы преобразуем его к более удобному и простому виду.
Шаг 1. Приведение к «неполному виду»: 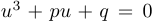 . Сделаем в приведенном уравнении замену
. Сделаем в приведенном уравнении замену 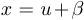 , где
, где 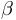 — некоторое число, которое нам предстоит определить. Подставив в уравнение, получим
— некоторое число, которое нам предстоит определить. Подставив в уравнение, получим 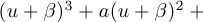
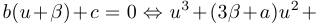
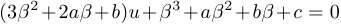 . Положив
. Положив 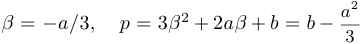 ,
, 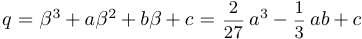 , мы и получим уравнение нужного нам вида, а именно,
, мы и получим уравнение нужного нам вида, а именно,
неполное уравнение 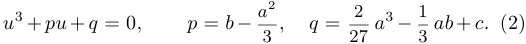
Пример 3.
Уравнение 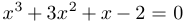 после замены
после замены 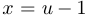 приводится к виду
приводится к виду 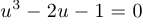 .
.
Частный случай. Если 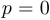 , то уравнение имеет единственное вещественное решение
, то уравнение имеет единственное вещественное решение 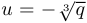 .
.
В дальнейшем будем предполагать, что 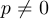 .
.
Шаг 2. Приведение к «нормальной форме»:  , где
, где 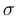 равно 3 или —3. В уравнении
равно 3 или —3. В уравнении 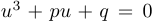 сделаем замену
сделаем замену 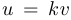 , где
, где 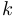 — некоторое число
— некоторое число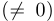 , которое нам предстоит определить. Подставив в уравнение, получим
, которое нам предстоит определить. Подставив в уравнение, получим 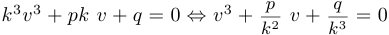 . Положим
. Положим
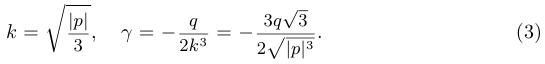
Теорема 1. Кубическое уравнение 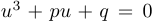 заменой
заменой 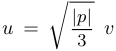 водится к нормальной форме вида
водится к нормальной форме вида  при
при 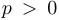 или
или 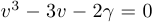 при
при 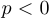 . При этом в обоих случаях
. При этом в обоих случаях 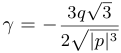 .
.
Пример 4.
Уравнение 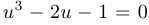 после замены
после замены 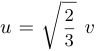 приводится к виду
приводится к виду 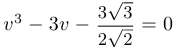 .
.
Шаг 3. Решение уравнения  . Сделаем еще одну замену:
. Сделаем еще одну замену: 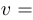
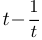 . После подстановки в уравнение получим:
. После подстановки в уравнение получим:  , где
, где 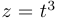 . Получившееся квадратное уравнение имеет корни
. Получившееся квадратное уравнение имеет корни 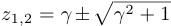 , которые удовлетворяют условию
, которые удовлетворяют условию 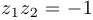 .
.
Обозначим 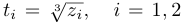 . Поскольку
. Поскольку 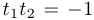 числа
числа 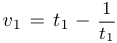 и
и 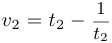 равны, следовательно, решение уравнения имеет вид
равны, следовательно, решение уравнения имеет вид
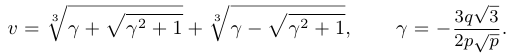
Пример 5.
Уравнение 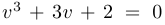 имеет единственное вещественное решение
имеет единственное вещественное решение
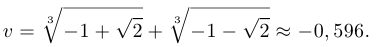
Шаг 4. Решение уравнения 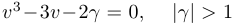 . Сделаем замену:
. Сделаем замену: 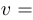
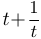 . После подстановки в уравнение получим:
. После подстановки в уравнение получим: 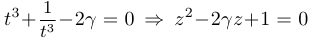 , где
, где 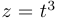 . Получившееся квадратное уравнение имеет корни
. Получившееся квадратное уравнение имеет корни 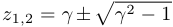 .
.
Обозначим 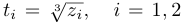 . Поскольку
. Поскольку 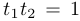 числа
числа 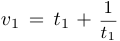 и
и 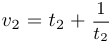 равны, следовательно, решение уравнения имеет вид
равны, следовательно, решение уравнения имеет вид
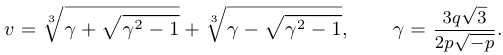
Пример 6.
Уравнение 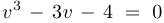 имеет единственное вещественное решение
имеет единственное вещественное решение
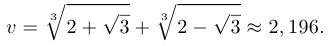
Частные случаи:
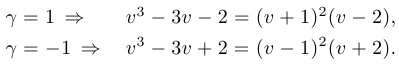
Шаг 5. Решение уравнения 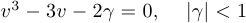 .
.
В этом случае замена имеет вид 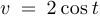 . Воспользовавшись формулой косинуса тройного угла (
. Воспользовавшись формулой косинуса тройного угла (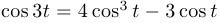 ) получим, что
) получим, что 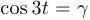 .
.
Обозначим  . Тогда
. Тогда
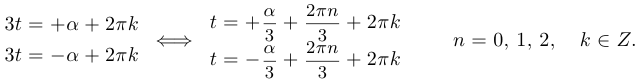
Таким образом, мы имеем шесть значений:
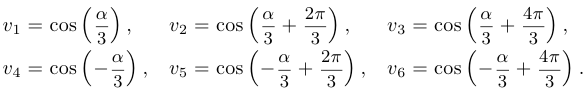
Однако, из свойств косинуса следует, что 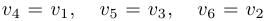 . Также несложно проверить, что поскольку
. Также несложно проверить, что поскольку 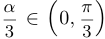 , числа
, числа 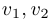 и
и 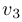 из различны. Они и составляют набор из трех корней уравнения.
из различны. Они и составляют набор из трех корней уравнения.
Пример 7.
Уравнение 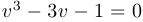 . Здесь
. Здесь
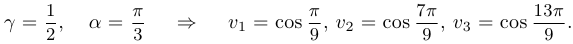
Решение уравнений четвертой степени.
Уравнением четвертой степени общего вида называется уравнение 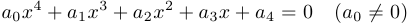 . Разделив обе части равенства на
. Разделив обе части равенства на 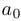 и обозначая для удобства
и обозначая для удобства 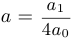 , получим
, получим
приведенное уравнение специального вида 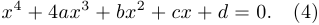
Нашей задачей является решение этого уравнения в вещественной области, то есть нахождение всех вещественных корней. На первых шагах мы преобразуем его к более удобному и простому виду.
Шаг 1. Приведение к «неполному виду»: 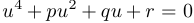 . Сделаем замену
. Сделаем замену 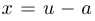 :
: 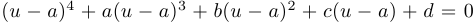 . После приведения подобных членов получим неполное уравнение
. После приведения подобных членов получим неполное уравнение 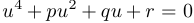 , где
, где

Пример 8.
Уравнение 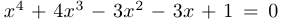 после замены
после замены 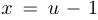 приводится к виду
приводится к виду 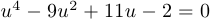 .
.
Частный случай. Если 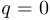 , то уравнение является биквадратным и решается заменой
, то уравнение является биквадратным и решается заменой 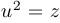 .
.
В дальнейшем будем предполагать, что 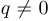 .
.
Шаг 2. Разложение на квадратичные множители. Каждый многочлен четвертой степени можно представить в виде произведения двух квадратичных. Мы покажем это для нашего случая «де факто», а именно, покажем, что найдутся вещественные числа 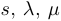 такие, что
такие, что
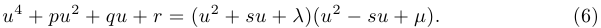
Для этих чисел должны выполняться равенства
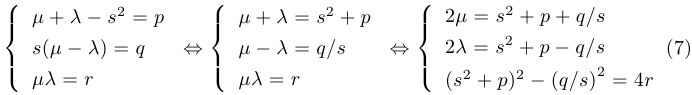
Шаг 3. Решение вспомогательного кубического уравнения. Обозначим 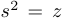 . Последнее уравнение системы 7 является кубическим относительно
. Последнее уравнение системы 7 является кубическим относительно 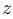 . Назовем его вспомогательным кубическим уравнением:
. Назовем его вспомогательным кубическим уравнением:
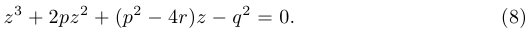
Заметим, что это уравнение всегда имеет положительный корень, поскольку при 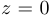 левая часть отрицательна, а при достаточно большом
левая часть отрицательна, а при достаточно большом 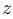 она положительна. Обозначим этот корень через
она положительна. Обозначим этот корень через 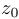 . Тогда
. Тогда 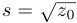 , а коэффициенты
, а коэффициенты 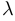 и
и 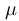 находятся по формулам 7. Таким образом, разложение 6 получено.
находятся по формулам 7. Таким образом, разложение 6 получено.
Пример 9.
Решить уравнение 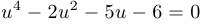 .
.
Решение:
Здесь 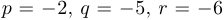 . Вспомогательное кубическое уравнение имеет вид
. Вспомогательное кубическое уравнение имеет вид 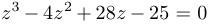 . Оно имеет положительный корень
. Оно имеет положительный корень 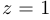 , следовательно,
, следовательно,
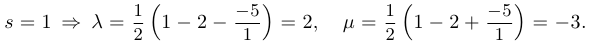
Таким образом, 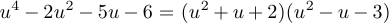 и корнями уравнения являются два вещественных числа
и корнями уравнения являются два вещественных числа 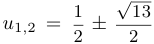 и два комплексных числа
и два комплексных числа 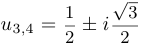 .
.
Пример 10.
Решить уравнение 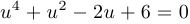 .
.
Решение:
Здесь 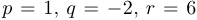 . Вспомогательное кубическое уравнение имеет вид
. Вспомогательное кубическое уравнение имеет вид 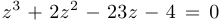 . Оно имеет положительный корень
. Оно имеет положительный корень 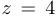 , следовательно,
, следовательно,
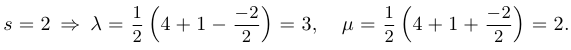
Таким образом, 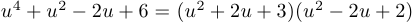 . Уравнение имеет четыре комплексных корня:
. Уравнение имеет четыре комплексных корня: 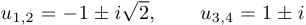 .
.
На этой странице найдёте другие готовые курсовые работы во высшей математике:
Много готовых курсовых работ по высшей математике
Можете посмотреть другие готовые курсовые работы по высшей математике:
| Курсовая работа на тему: системы линейных уравнений |
| Курсовая работа на тему: комплексные числа |
| Курсовая работа на тему: выпуклые множества и функции |
| Курсовая работа на тему: оптимизационные задачи |

