Оглавление:
Определение предела последовательности можно считать частным случаем определения предела функции на бесконечности (при 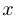 , стремящемся к
, стремящемся к  ), поскольку значения
), поскольку значения 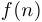 образуют последовательность, которая тем более будет стремиться к
образуют последовательность, которая тем более будет стремиться к 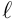 , если
, если  .
.
Число 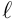 называется пределом функции
называется пределом функции 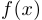 при
при 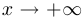 , если
, если
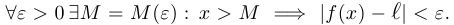
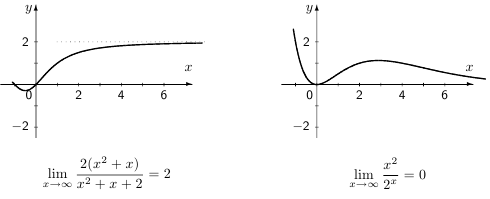
При этом, разумеется, естественно считать, что имеет смысл говорить о том, что 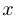 стремится к бесконечности, лишь когда область определения не является ограниченным множеством. Прежде чем перейти к случаю, когда
стремится к бесконечности, лишь когда область определения не является ограниченным множеством. Прежде чем перейти к случаю, когда 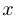 стремится к конечному числу, введем несколько вспомогательных понятий.
стремится к конечному числу, введем несколько вспомогательных понятий.
Замыкание множества.
Окрестностью точки 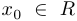 называется любой интервал
называется любой интервал 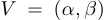 , содержащий точку
, содержащий точку 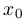 , или любое множество, содержащее такой интервал,
, или любое множество, содержащее такой интервал, 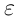 -окрестностью точки
-окрестностью точки 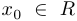 называется интервал
называется интервал  . Проколотой окрестностью точки
. Проколотой окрестностью точки 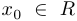 называется окрестность
называется окрестность 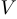 без самой точки, то есть множество
без самой точки, то есть множество 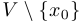 .
.
Пусть 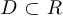 . Будем говорить, что точка
. Будем говорить, что точка 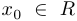 является точкой сгущения, или предельной точкой, множества
является точкой сгущения, или предельной точкой, множества 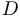 , если в любом интервале (
, если в любом интервале (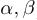 ), содержащем точку
), содержащем точку 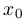 , найдется хотя бы одна другая точка множества
, найдется хотя бы одна другая точка множества 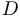 . Если точка множества не является точкой сгущения этого множества, то она называется изолированной. Объединение множества
. Если точка множества не является точкой сгущения этого множества, то она называется изолированной. Объединение множества 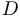 и множества его точек сгущения называется замыканием множества
и множества его точек сгущения называется замыканием множества 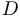 и обозначается через
и обозначается через 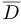 . Для множества точек сгущения нет специального обозначения, но это множество получится, если из замыкания множества выкинуть все изолированные точки. Говорят также, что бесконечность является предельной точкой множества
. Для множества точек сгущения нет специального обозначения, но это множество получится, если из замыкания множества выкинуть все изолированные точки. Говорят также, что бесконечность является предельной точкой множества 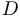 , если
, если 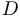 не является ограниченным.
не является ограниченным.
Если некоторая точка не является предельной для области определения функции, то в ней понятие предела этой функции не имеет смысла.
Пример 1.
Пусть: 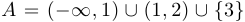 ,
, 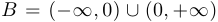 ,
, 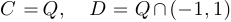 . Тогда:
. Тогда: 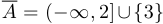 ,
, 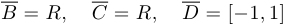 . При этом множество точек сгущения множества
. При этом множество точек сгущения множества 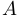 совпадает с
совпадает с 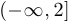 . Для
. Для 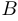 ,
, 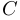 и
и 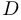 множество точек сгущения совпадает с их замыканиями. Бесконечность является предельной точкой для множеств
множество точек сгущения совпадает с их замыканиями. Бесконечность является предельной точкой для множеств 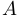 ,
, 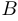 и
и 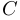 .
.
Предел функции. Пусть 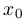 — точка сгущения множества
— точка сгущения множества 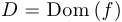 .
.
Число 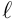 называется пределом функции
называется пределом функции 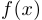 при
при 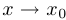 , если
, если
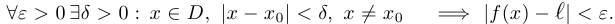
Число 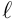 является пределом функции
является пределом функции 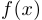 при
при  (пределом функции справа), если
(пределом функции справа), если
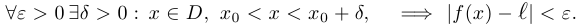
Аналогично определяется предел функции слева и на бесконечности.
Число 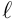 называется пределом функции
называется пределом функции 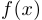 при
при 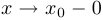 (пределом функции слева), если
(пределом функции слева), если
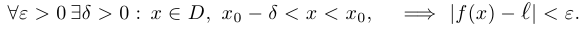
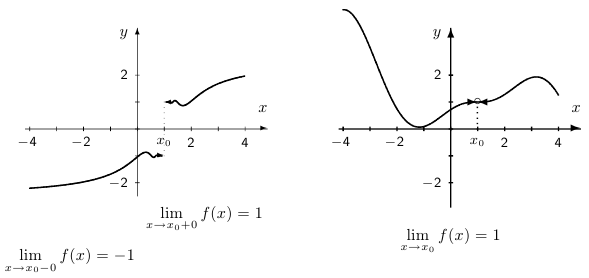
Говорят, что функция 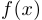 стремится к + бесконечности при
стремится к + бесконечности при 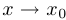 , если
, если
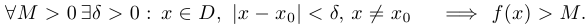
Теорема об арифметических операциях с пределами. Если функции 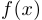 и
и 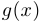 имеют предел в точке хо, то функции
имеют предел в точке хо, то функции 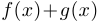 ,
, 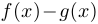 ,
, 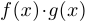 также имеют предел, причем:
также имеют предел, причем:
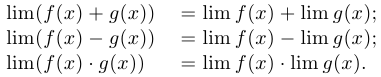
Все то же самое верно и для отношения 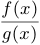 , но при дополнительном предположении, что
, но при дополнительном предположении, что 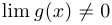 .
.
Дробно-рациональной функцией называется функция вида 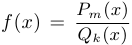 , где
, где 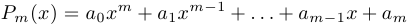 ,
, 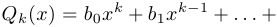
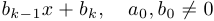 .
.
Теорема о дробно-рациональной функции.
Пусть 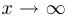 . Тогда: если
. Тогда: если 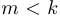 , то
, то 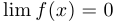 ;
;
если 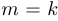 , то
, то 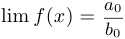 ;
;
если 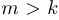 , то
, то 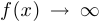 .
.
Пусть 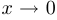 . Тогда: если
. Тогда: если 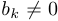 , то
, то 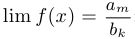 ;
;
если 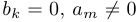 , то
, то 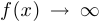 .
.
Пример 2.

Теорема о переходе к пределу в неравенстве. Если функции 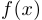 и
и 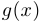 имеют предел в некоторой точке и
имеют предел в некоторой точке и 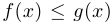 в какой-либо окрестности этой точки, то в этой точке
в какой-либо окрестности этой точки, то в этой точке 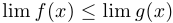 .
.
Теорема о сжатой функции. Пусть три функции 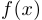 ,
, 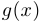 и
и 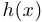 в некоторой окрестности точки
в некоторой окрестности точки 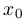 удовлетворяют неравенствам
удовлетворяют неравенствам 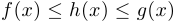 . Если функции
. Если функции 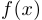 и
и 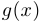 имеют предел в этой точке и при этом
имеют предел в этой точке и при этом 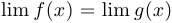 , то функция
, то функция 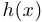 также имеет предел и
также имеет предел и 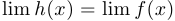 .
.
Ограниченные, бесконечно малые и бесконечно большие.
Функция 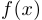 называется бесконечно малой в точке
называется бесконечно малой в точке 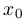 , если
, если 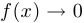 при
при 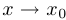 .
.
Функция 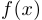 называется ограниченной на интервале (
называется ограниченной на интервале (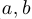 ), если
), если 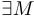 такое, что
такое, что 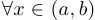 верно неравенство
верно неравенство 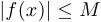 .
.
Функция 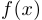 называется ограниченной в окрестности точки
называется ограниченной в окрестности точки 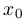 , если существует интервал, содержащий точку
, если существует интервал, содержащий точку 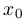 , такой, что
, такой, что 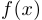 ограничена на этом интервале.
ограничена на этом интервале.
Утверждение. Произведение функции, бесконечно малой в некоторой точке, на ограниченную в окрестности этой же точки есть бесконечно малая в этой точке функция.
Функция 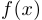 называется бесконечно большой в точке
называется бесконечно большой в точке 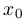 , если
, если 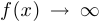 при
при 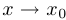 .
.
Утверждение. Произведение бесконечно малой на ограниченную есть бесконечно малая. Если ограниченную разделить на бесконечно большую, то получится бесконечно малая.
Примеры бесконечно малых функций:
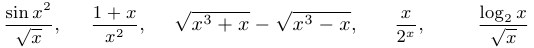 при
при 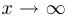 ;
;
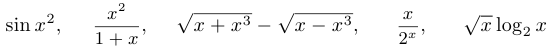 при
при 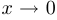 ;
;
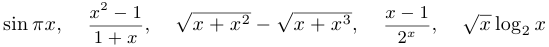 при
при 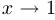 .
.
Примеры бесконечно больших функций:
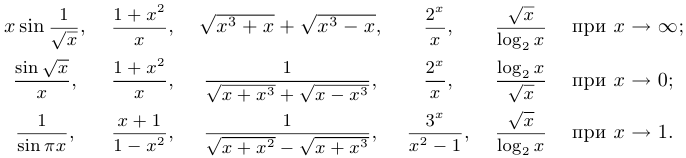
Эквивалентные функции.
Две функции 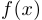 и
и 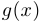 называются эквивалентными в точке
называются эквивалентными в точке 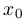 , если существует предел
, если существует предел 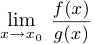 и если этот предел равен 1. При этом мы пишем:
и если этот предел равен 1. При этом мы пишем: 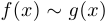 при
при 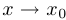 .
.
Две функции 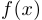 и
и 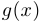 будем называть эквивалентными в точке
будем называть эквивалентными в точке 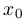 с точностью до постоянной (с точностью до постоянного множителя), если существует предел
с точностью до постоянной (с точностью до постоянного множителя), если существует предел 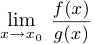 и если этот предел не равен 0. Обозначив этот предел через
и если этот предел не равен 0. Обозначив этот предел через 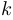 , получим, что
, получим, что 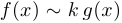 при
при 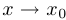 .
.
Замечательные пределы.
Два предела принято называть замечательными:

Иногда замечательными называют также соотношения, являющиеся следствиями указанных двух:
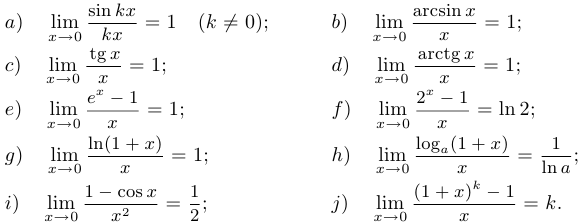
Символ Ландау.
Если 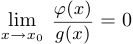 , то говорят, что функция
, то говорят, что функция 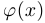 есть
есть 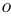 -маленькое от
-маленькое от 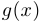 при
при 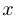 , стремящемся к
, стремящемся к 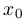 и пишут:
и пишут: 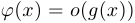 при
при 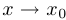 . Значок «
. Значок «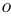 » называется символом Ландау.
» называется символом Ландау.
Примеры:  при
при 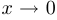 ,
, 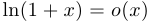 при
при 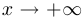 .
.
Если обе функции 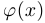 и
и 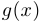 являются бесконечно малыми в точке
являются бесконечно малыми в точке 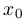 , то говорят, что
, то говорят, что 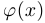 является бесконечно малой более высокого порядка, чем
является бесконечно малой более высокого порядка, чем 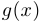 .
.
Примеры: 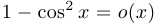 при
при 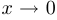 ,
, 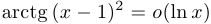 при
при 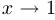 .
.
Теорема о выделении линейной части. Пусть функции 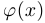 и
и 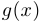 определены в некоторой окрестности точки
определены в некоторой окрестности точки 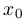 и при этом в точке
и при этом в точке 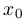 существует предел
существует предел 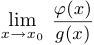 . Обозначим этот предел через
. Обозначим этот предел через 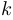 . Тогда
. Тогда
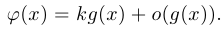
Выражение 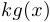 и называется линейной частью функции
и называется линейной частью функции 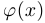 относительно
относительно 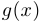 . В частности, запись «
. В частности, запись «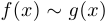 при
при 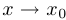 » эквивалентна записи «
» эквивалентна записи «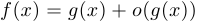 при
при 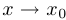 ».
».
Примеры: 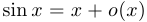 при
при 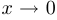 ,
, 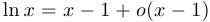 при
при 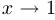 .
.
Ниже приведены примеры нескольких наиболее часто встречающихся эквивалентностей при 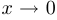 .
.
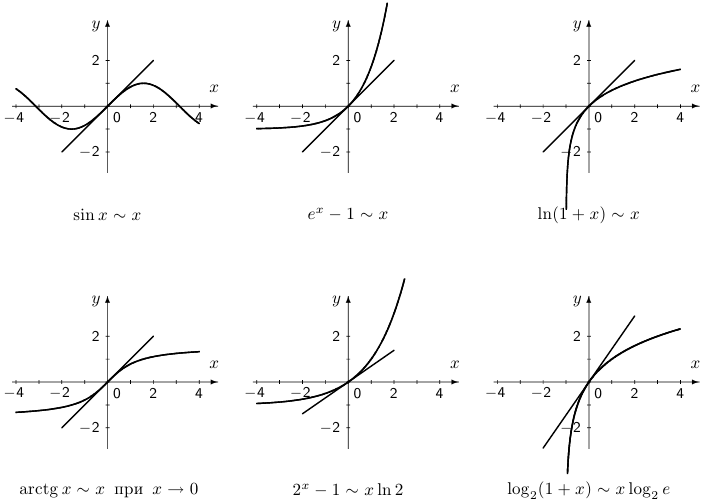
Упр. 1. В каждом из рассмотренных примеров укажите также предел отношения двух функций при 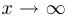 .
.
Теорема о замене на эквивалентную под знаком предела. Если 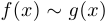 при
при 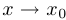 , то:
, то:
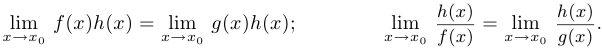
Пример 3.
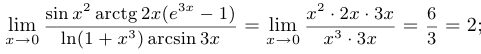
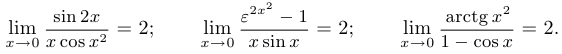
Пример 4.
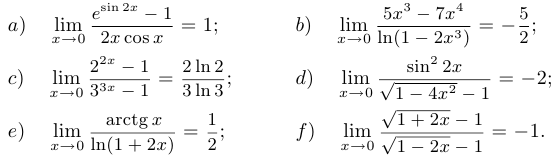
Определение предела на языке последовательностей.
Определение предела, которое было дано в начале главы принято называть определением на языке эпсилон-дельта или на языке Коши.
Иногда удобно использовать и другое, эквивалентное определение, которое называют определением на языке последовательностей или на языке Гейне (в честь немецкого математика XIX века).
Число 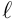 является пределом функции
является пределом функции 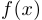 при
при 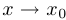 , если для любой последовательности
, если для любой последовательности 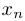 , стремящейся к
, стремящейся к 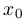 , такой, что
, такой, что 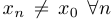 , верно, что
, верно, что 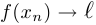 при
при  .
.
Прежде чем продемонстрировать на примере, как используется эквивалентность двух определений предела, приведем без доказательства еще одно важное соотношение:
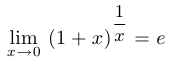
Подставив в указанное соотношение последовательность 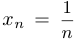 , получим уже доказанное ранее соотношение
, получим уже доказанное ранее соотношение 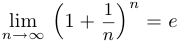 .
.
Пример 5.
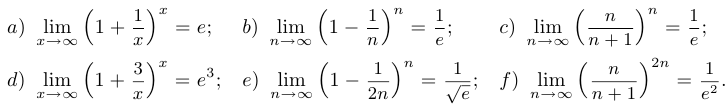
Непрерывность функции.
Функция 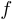 называется непрерывной в точке
называется непрерывной в точке  , если предел в этой точке существует (в случае, если
, если предел в этой точке существует (в случае, если  — точка сгущения множества
— точка сгущения множества 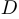 ) и равен значению функции в этой точке.
) и равен значению функции в этой точке.
Если  — изолированная точка множества
— изолированная точка множества 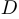 , то мы будем считать функцию непрерывной в этой точке (это вопрос чисто формальной договоренности).
, то мы будем считать функцию непрерывной в этой точке (это вопрос чисто формальной договоренности).
Если пределы слева и справа существуют, то у непрерывной функции они должны быть равны между собой.
Таким образом, предел непрерывной функции в точке равен значению функции в точке. Вспоминая определение предела функции в точке мы можем дать «явное» определение непрерывности.
Функция 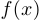 называется непрерывной в точке
называется непрерывной в точке  , если
, если
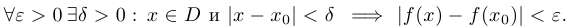
Эквивалентное определение можно дать и на языке последовательностей.
Функция 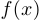 называется непрерывной в точке
называется непрерывной в точке  , если для любой последовательности
, если для любой последовательности 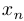 , стремящейся к
, стремящейся к  , верно, что
, верно, что 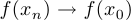 при
при 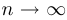 .
.
Понятие непрерывности достаточно естественно.
В частности, тем, что выполняются простые условия, обеспечивающие работу с непрерывными функциями.
Теорема об арифметических операциях замене с непрерывными функциями. Если 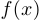 и
и 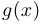 — функции, непрерывные в точке
— функции, непрерывные в точке  , то в этой же точке непрерывны функции
, то в этой же точке непрерывны функции 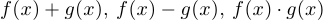 , а также
, а также 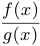 , при дополнительном предположении, что
, при дополнительном предположении, что 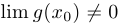 .
.
Теорема о непрерывности суперпозиции. Если функция 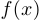 непрерывна в точке
непрерывна в точке  , а
, а 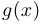 непрерывна в точке
непрерывна в точке 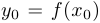 , то в точке
, то в точке  непрерывна функция
непрерывна функция  .
.
Функция 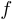 называется непрерывной на множестве
называется непрерывной на множестве 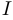 , если она непрерывна в каждой точке этого множества.
, если она непрерывна в каждой точке этого множества.
Для множества функций, непрерывных на промежутке 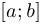 принято следующее обозначение:
принято следующее обозначение: 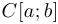 . Таким образом, запись
. Таким образом, запись 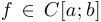 означает, что функция
означает, что функция 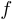 определена и непрерывна на отрезке
определена и непрерывна на отрезке 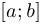 .
.
Теорема о непрерывности обратной функции. Если 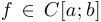 и у
и у 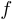 существует обратная функция
существует обратная функция 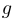 , то
, то 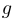 непрерывна на
непрерывна на 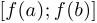 (или
(или 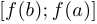 , если
, если 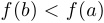 ).
).
Пример 6.
Дробно-рациональная функция 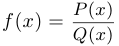 непрерывна в каждой точке
непрерывна в каждой точке  вещественной прямой, в которой
вещественной прямой, в которой 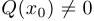 .
.
Пример 7.
Функции 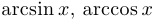 и
и 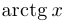 непрерывны на своих областях определения, то есть на промежутках
непрерывны на своих областях определения, то есть на промежутках 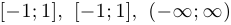 .
.
Пример 8.
Функции 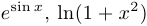 , и
, и 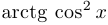 непрерывны на всей вещественной прямой.
непрерывны на всей вещественной прямой.
Также без доказательства сформулируем еще две важные теоремы об ограниченности непрерывных функций на замкнутом промежутке.
1-я теорема Вейерштрасса. Если функция определена и непрерывна на промежутке 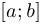 , то она ограничена на этом промежутке.
, то она ограничена на этом промежутке.
Карл Вейерштрасс (Karl Weierstras, 1815 — 1897) — выдающийся немецкий математик, «отец современного анализа». Занимался теорией аналитических функций. В значительной степени ему мы обязаны современными формулировками теорем, ставших классическими, крылатой фразой «нельзя быть настоящим математиком, не будучи немного поэтом», а также славой Софьи Ковалевской.
2-я теорема Вейерштрасса. Если функция определена и непрерывна на промежутке 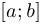 , то в некоторых точках этого промежутка она принимает свои наибольшее и наименьшее значения.
, то в некоторых точках этого промежутка она принимает свои наибольшее и наименьшее значения.
Пример 9.
а) Функция 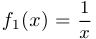 определена и непрерывна на
определена и непрерывна на  , однако не является ограниченной на этом промежутке;
, однако не является ограниченной на этом промежутке;
b) Функция 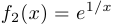 при
при 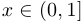 ,
, 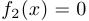 при
при 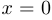 , определена на
, определена на 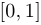 , однако не является ограниченной на этом промежутке;
, однако не является ограниченной на этом промежутке;
c) Функция 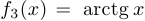 определена и непрерывна на
определена и непрерывна на 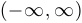 , является ограниченной на этом промежутке, но не принимает ни в какой точке наибольшее или наименьшее значения.
, является ограниченной на этом промежутке, но не принимает ни в какой точке наибольшее или наименьшее значения.
Следующая теорема иногда называется теоремой о промежуточном значении. Она была доказана Больцано в 1817 году и позже Коши в 1821 году.
Теорема Больцано (Больцано — Коши). Пусть дана непрерывная функция на отрезке 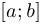 (
(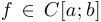 ). причем
). причем 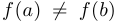 . Без ограничения общности предположим, что
. Без ограничения общности предположим, что 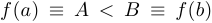 . Тогда для любого
. Тогда для любого 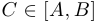 существует
существует 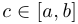 такое, что
такое, что 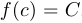 .
.
Следующее важное следствие иногда называют 1-й теоремой Больцано — Коши: Если функция принимает в концах отрезка значения разных знаков, то существует точка, в которой она равна нулю.
Пример 10.
Многочлены 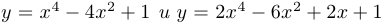 имеют по 4 корня, расположенных в интервалах
имеют по 4 корня, расположенных в интервалах 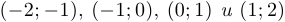 .
.
Действительно, в обоих случаях числа 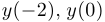 и
и 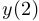 положительны, а
положительны, а 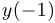 и
и 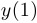 отрицательны.
отрицательны.
Точки разрыва. Говорят, что в точке  функция имеет устранимый разрыв, если существует предел функции в этой точке, однако само значение функции в этой точке либо не определено, либо не совпадает с этим пределом. Говорят, что в точке
функция имеет устранимый разрыв, если существует предел функции в этой точке, однако само значение функции в этой точке либо не определено, либо не совпадает с этим пределом. Говорят, что в точке  функция имеет разрыв 1 рода, или скачок, если пределы функции в этой точке слева и справа существуют и различны. Во всех остальных случаях говорят, что функция имеет разрыв 2 рода.
функция имеет разрыв 1 рода, или скачок, если пределы функции в этой точке слева и справа существуют и различны. Во всех остальных случаях говорят, что функция имеет разрыв 2 рода.
На этой странице найдёте другие готовые курсовые работы во высшей математике:
Много готовых курсовых работ по высшей математике
Можете посмотреть другие готовые курсовые работы по высшей математике:
| Курсовая работа на тему: элементы комбинаторики |
| Курсовая работа на тему: числовые последовательности |
| Курсовая работа на тему: производная |
| Курсовая работа на тему: монотонность и экстремумы |

