Логические функции

Самым простым множеством, на котором можно задать нетривиальные функции, является двухточечное множество. Пусть этими двумя точками являются символы «О» и «1».

Одноместные функции на двухточечном множестве.

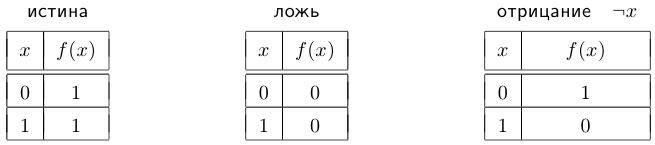
Рассмотрим множество 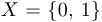и все возможные функции, заданные на нем и принимающие те же значения. Таких функций, кроме тождественной, всего три: две постоянные и одна — меняющая значение. Они имеют соответствующие названия: истина, ложь и отрицание. Задать эти функции можно с помощью так называемых таблиц истинности, то есть буквальным указанием, какое значение принимает функция в каждой точке.

Двуместные функции.

Двуместные функции являются функциями двух переменных, или, как говорят, функциями с областью определения, являющейся прямым произведением множеств, которые пробегает каждая из переменных. В данном случае 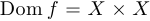. Все двуместные функции имеют также свои названия и также задаются таблицами истинности.

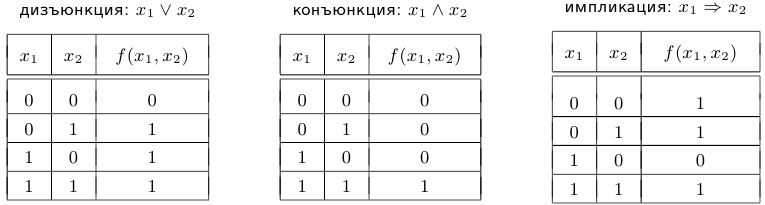
Отметим еще раз, что «1» и «О» являются в данном случае символами и могут быть заменены любыми другими символами, например «t» (true) и «f» (false), или соответственно на русском языке — «и» (истина) и «л» (ложь).

Разговор о логике, который можно пропустить. Логики бывают разные: бытовая логика, «железная», диалектическая и другие. Существует логика того языка, на котором мы говорим, и эта логика подчиняется другим законам, нежели математическая. Например, истинность отрицания отрицания далеко не всегда совпадает с истинностью самого высказывания, принадлежность на бытовом языке означает не то же самое, что принадлежность в математической логике, и так далее.

Но главное, что различает эти логики, — это формальная цель, правила вывода и критерий возможности их использования. Для математической логики таким критерием являются формальные понятия истины (и) и лжи (л), а целью — выводимость формул. Для логики факта, например, критерием является «было» или «не было», а целью — построение той или иной классификации фактов. Для логики убеждений, с которой, к сожалению, мы сталкиваемся чаще, чем с другими типами логик, целью является победа в споре, а используемые правила считаются хорошими (корректными в рамках данной логики), если они достигают этой цели.

Логики различаются и используемыми языками; и принципиальное различие между языком математической логики и языком человеческого общения состоит, в частности, в том, что первый оперирует с так называемыми атомами, элементарными высказываниями, о которых мы можем договориться: истинны они или ложны. Во втором же случае мы работаем с понятиями, которые далеко не всегда конечнозначны и, более того, как правило, имеют множество неустранимых оттенков.

Другое существенное различие, с которого мы и начнем, состоит в характере используемых определений. В «обычной» логике мы определяем или стараемся определить (или делаем вид, что стараемся определить) все используемые понятия, и зачастую эти определения разнородны даже в рамках одного и того же текста: иногда они носят описательный характер, иногда указывают лишь характерные свойства объекта, иногда правила его функционирования. Кроме того, одним из характерных недостатков при построении той или иной теории является «порочный круг» — так называется цепочка определений, в которой некоторый термин определяется с использованием других, которые, в свою очередь, описываются с помощью третьих, и так далее, пока в цепочке определений вновь не появится первоначальное понятие. Это не всегда плохо в обычном языке, однако в математической логике это недопустимо. Поэтому в математике существует целый ряд «аксиоматических», неопределяемых понятий, из которых конструируются остальные.

Атомарные высказывания.

Одним из способов получать высказывания, то есть фразы, о которых можно определенно сказать, истинны они или ложны, является дедуктивный метод, то есть метод построения сложных высказываний из простейших или атомарных.

Атомарным (элементарным) высказыванием мы называем фразу, приписывание которой одного из двух значений, «и» или «л», либо заранее объявлено, либо вытекает из смысла этой фразы и не вызывает сомнений ни у кого из тех, кто эту фразу читает. Например, высказывания 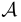: {Идет дождь) и 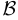: {Я сижу дома) мы не можем считать, вообще говоря, высказываниями, к которым применимы правила формальной логики, поскольку не определено время действия, а в первом случае и место действия. Тем не менее возможно составить сложное или составное высказывание типа 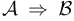: {Если завтра будет идти дождь, то я буду сидеть дома.)

Используемые в обычной жизни простые высказывания, в отличие от математических, редко являются «абсолютными», то есть такими, что их истинность или ложность бесспорна и однозначна во все времена, при любых обстоятельствах. Такое отличие объясняется тем, что бытовые понятия редко бывают абсолютно отчетливыми. Например, не всегда точно мы сможем определить, был дождь или нет, именно сегодня или нет. Кроме того, противоречивость может быть и «внутренней», при всей кажущейся отчетливости самих понятий.

Софизм «деревенский парикмахер».

Рассмотрим деревенского парикмахера, который бреет всех тех, и только тех, которые не бреются сами. Является ли высказыванием (то есть можно ли сказать, истинно оно или нет) следующее утверждение (Деревенский парикмахер бреет себя сам)?

Софизм Эпименида (VI в. до н.э. для понимания софизма необходимо знать, что Эпименид — житель Крита.). Истинно или нет следующее высказывание Эпименида (Все критяне — лжецы)?

Парадокс Эвбулида (IV в. до н.э.). Истинно или нет следующее высказывание (Высказывание, которое я сейчас произношу, ложно)?

Сложное высказывание. Сложным, или составным, высказыванием мы называем высказывание, которое можно получить из атомарных высказываний с помощью логических операций. Например:

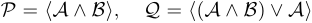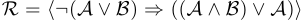, — являются составленными из атомарных высказывани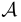й и 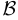с помощью указанных логических операций.

Таблицы истинности позволяют узнать, какие значения принимают указанные высказывания в зависимости от значений высказывани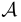й и .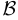

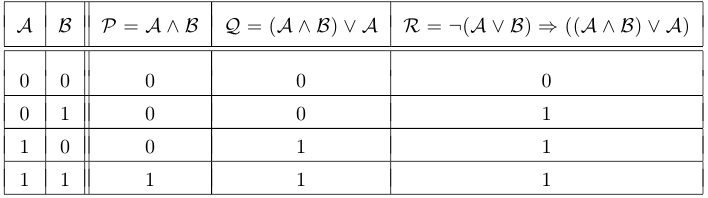
Сложные высказывания мы называем эквивалентными, если на множестве значений переменных — элементарных высказываний — они принимают одинаковые значения.

Из построенной выше таблицы мы можем заключить, что и .

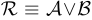Высказывания и высказывательные функции.

Некоторые фразы не являются высказываниями, однако содержат переменную, которой можно приписать то или иное значение, после чего фраза становится высказыванием. Например, фраза 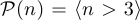зависит от переменной 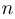, и, пока значение этой переменной не указано, нельзя ничего сказать про истинность. В таких случаях говорят, что задана высказывательная функция. В данном примере высказывательная функция 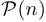является функцией одной переменной, но, разумеется, легко построить и функции двух, трех, нескольких переменных. Например, 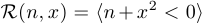. Перейти от высказывательной функции к высказыванию можно несколькими способами, из которых первый — самый обычный.

1°. Взятие значения функции в конкретной точке. Например, 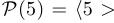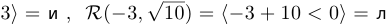. Пишут также .

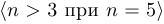2°. Переход от высказывательной функции 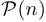к высказыванию, которое истинно в том и только в том случае, когда существует конкретное значение 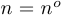из области определения функции такое, что 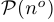является верным высказыванием. Этот переход обозначается так: 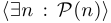. Символ (значок) 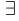называется квантором существования, а сам переход — операцией связывания переменной с помощью квантора существования или — несколько упрощенно — операцией навешивания квантора существования. Например, 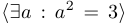. Читается это так: «Существует 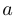такое, что 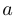в квадрате равно трем». Навешивание квантора существования можно произвести и для функций нескольких переменных. При этом иногда ставится двойной квантор, чтобы подчеркнуть множественное число. Например, 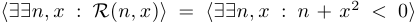. Читается это так: «Существуют 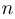и 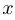такие, что ».

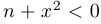Последнее утверждение не вполне корректно: не слишком понятно, какое 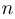можно брать. Чтобы избавиться от этой неопределенности, обычно сразу указывают область определения переменной. При этом значение высказывания может, разумеется, измениться в зависимости от выбора области определения. Например, 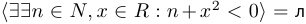. . 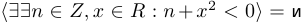Кроме того, квантор существования можно навешивать поочередно, причем не важно, в каком порядке: .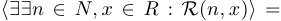

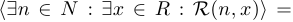
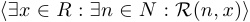3°. Переход от высказывательной функции 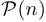к высказыванию, которое истинно в том и только в том случае, когда для всех значений переменной 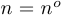из области определения 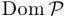функции 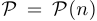верно конкретное высказывание 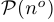. Этот переход обозначается так: 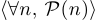. Символ 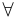называется квантором общности. Например, 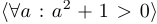. Читается это так: «Для любого а верно, что а в квадрате плюс один больше нуля.»

При работе с кванторными высказываниями можно использовать ряд свойств и соглашений.

Соглашения

1. Соглашение об области определения. Если из контекста ясно, о какой области определения идет речь, то указание на нее можно опустить.

Например, 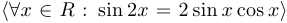то же самое, что и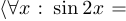 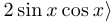. Обычно это делают в том случае, когда высказывательная функция является тождественно истинной на области определения. Однако не стоит убирать область определения в высказывании .

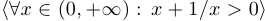2. Соглашение о кванторе общности. Квантор общности, стоящий снаружи (впереди), можно опустить, если перед этим было реализовано первое из соглашений об области определения. Например, высказывание 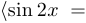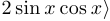обычно воспринимается как тождество, справедливое без всяких ограничений.

3. Соглашение о скобках и знаках препинания. Скобки, внутри которых стоит ограничение на переменную, можно опустить. Треугольные (или фигурные) скобки, которыми заключена высказывательная функция, можно заменить круглыми или квадратными или опустить вовсе, отделив высказывательную функцию от ограничений вертикальной чертой или двоеточием. Запятые при этом обычно не ставятся. Например, .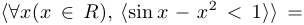

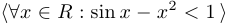Свойства кванторов

1. Одноименные соседние кванторы в простом кванторном высказывании можно переставлять.

Например: .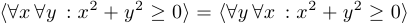

2. При перенесении (перестановке) квантора общности налево получается высказывание, являющееся следствием первоначального. То есть либо значение высказывания не изменится, либо ложное станет истинным. Например: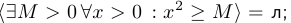

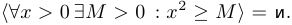
При перенесении (перестановке) квантора существования налево первоначальное высказывание является следствием полученного. То есть либо значение высказывания не изменится, либо истинное станет ложным. Например: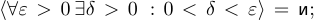

На этой странице найдёте другие готовые курсовые работы во высшей математике:

Много готовых курсовых работ по высшей математике

Можете посмотреть другие готовые курсовые работы по высшей математике:

Курсовая работа на тему: Множества и операции с ними

Курсовая работа на тему: функции

Курсовая работа на тему: метод математической индукции

Курсовая работа на тему: элементы комбинаторики