Задание: Нахождение определённых интегралов методом но частям.
Цель: формирование умения находить определённые интегралы методом по частям.
Задание для самостоятельной внеаудиторной работы:
28.1. Разберите, в чём заключается сущность использования метода по частям в определённом интеграле.
28.2. Найдите определённые интегралы методом по частям:
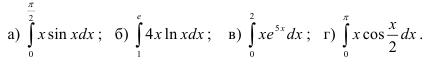
Готфрид Лейбниц был не только гениальным математиком, но ещё и талантливым изобретателем. Вам, как : студентам компьютерных специальностей, известно, что первую механическую счетную машину сконструировал в 1642 г. французский ученый Блез Паскаль. Машина Паскаля могла только складывать и вычитать.
Лейбниц пытался сначала лишь улучшить машину Паскаля, но понял, что для выполнения операций умножения и деления необходим совершенно иной принцип. Можно понять гордость Лейбница, писавшего впоследствии «Мне посчастливилось построить такую арифметическую машину, которая совершенно отлична от машины Паскаля, поскольку дает возможность мгновенно выполнять умножение и деление над огромными числами». Арифметическая машина Лейбница была первой в мире машиной, предназначенной для выполнения четырех действий арифметики.
Интересно, что один из первых экземпляров «арифметического инструмента» Лейбниц намеревался подарить Петру /, но машина оказалась неисправной, а механик ученого не смог ее починить в короткий срок. Лейбница живо интересовал молодой царь далекой Московии, которого он считал выдающимся реформатором. Петр встречался и переписывался с Лейбницем, обсуждал с ним проект организации Академии наук в Петербурге и развертывания системы образования в России.
Выполнив задание 28.2 и заменив получившиеся ответы буквами из таблицы, Вы узнаете, в каком году Лейбницем была сконструирована первая счётная машина для умножения и деления.
Год:
Карта ответов:
28.3. Найдите определённые интегралы:
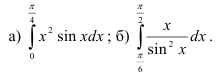
Методические указания по выполнению работы:
Интегрирование по частям — осуществляется с использованием формулы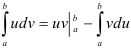 
.
Рекомендации по выбору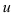 
и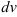 
, а также алгоритм нахождения интеграла методом по частям были подробно разобраны в методических указаниях к выполнению задания №21.
Рассмотрим примеры применения метода интегрирования по частям в определенном интеграле.
Пример 1.
Найдите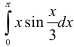 
.
Решение:
1. Исходный интеграл имеет вид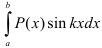 
, следовательно, за 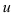принимаем многочлен 
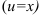, остальные множители примем за 
.
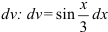2. Находим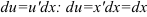 
.
Находим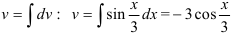 
(интеграл от некоторой сложной функции, полагаем 
).
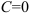3. По формуле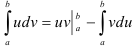 
имеем:
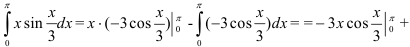
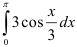. Преобразуем каждое слагаемое отдельно:
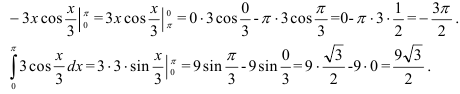
Тогда исходный интеграл равен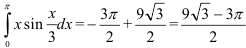 
.
Ответ: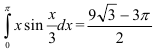 
.
На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:
Готовые контрольные работы по высшей математике
Обратите внимание на похожие контрольные работы возможно они вам будут полезны:
