Оглавление:
Задание: Решение задач на нахождение производных высших порядков, раскрытие неопределенностей по правилу Лопиталя.
Цель: формирование умения находить производные высших порядков, вычислять пределы функций, раскрывая неопределенности по правилу Лопиталя.
Задание для самостоятельной внеаудиторной работы:
14.1. Выучите определение производной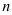 
-го порядка. Проанализируйте, как найти производную второго, третьего и четвертого порядков.
14.2. Найдите вторую производную функции:
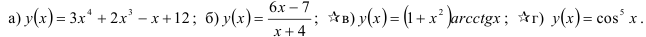
14.3. Найдите третью производную функции:
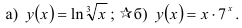
14.4. Найдите четвертую производную функции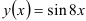 
.
14.5. Выясните, сколько раз нужно продифференцировать функцию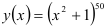 
, чтобы в результате получился многочлен тридцатой степени.
14.6. Запомните, в каких случаях используется правило Лопиталя. Выясните, как оно применяется.
14.7. Установите правильную последовательность косточек математического домино и Вы узнаете титул французского математика Гийома Франсуа Антуана де Лопиталя (1661 — 1704):
- автора первого печатного учебника по дифференциальному исчислению;
- учёного, в честь которого назван приём раскрытия неопределённостей вида
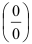или 
.
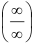Методические указания но выполнению работы:
Для успешного решения задач необходимо знание следующего теоретического материала:
I. Понятие производной высших порядков
Пусть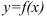 
— дифференцируемая на интервале 
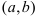функция. Тогда ее производная 
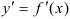— тоже функция, определенная на интервале 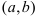. И у нее можно найти производную, называемую производной второго порядка или второй производной. Итак, производная от первой производной 
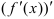называется второй производной функции и обозначается 
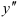или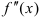 
.
Пример 1.
Найдите вторую производную функции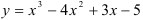 
.
Решение:
Найдем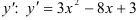 
.
Найдем 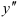как производную от 
.
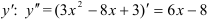Ответ: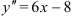 
.
Вторая производная — тоже представляет собой функцию, следовательно, существует производная второй производной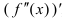 
, называемая третьей производной или 
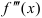. Так, в примере 1. 
.
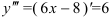Аналогично вводится определение четвертой производной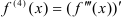 
;
пятой производной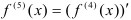 
;
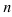-й производной 
.
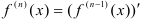Таким образом, производной 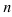-го порядка функции 
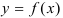называется производная от производной 
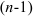-ro порядка (если она существует).
Пример 2.
Найдите четвертую производную функции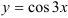 
.
Решение:
Найдем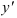 
как производную сложной функции 
:
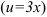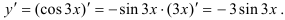
Найдем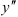 
как производную от 
.
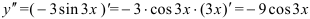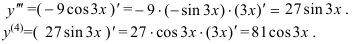
Ответ: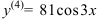 
.
Пример 3.
Найдите 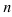-ю производную функции 
.
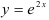Решение:
Найдем 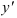как производную сложной функции 
:
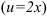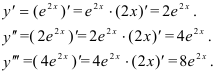
Очевидно, что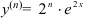 
.
Ответ: .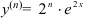
II. Правило Лопиталя
Если при вычислении предела функции возникает неопределенность вида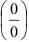 
или вида 
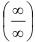, и никакой из существующих приемов ее раскрытия не работает, на помощь придет правило Лопиталя. Под правилом Лопиталя понимают прием раскрытия неопределенностей вида 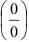или .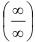
Теорема (правило Лопиталя). Для вычисления предела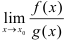 
, где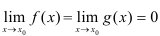 
, где достаточно найти предел отношения производных данных функций (если он существует), т.е. 
.
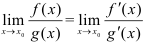Замечание. 1. Правило Лопиталя справедливо также для случаев
- неопределенности вида 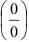при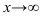
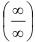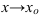; - неопределенности вида при
и .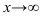
2. Правило Лопиталя может быть применено последовательно несколько раз для раскрытия неопределенностей вида 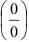или .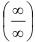
Рассмотрим примеры нахождения пределов функций с использованием правила Лопиталя.
Пример 4.
Вычислите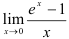 
.
Решение. Поскольку в примере встречается неопределенность вида 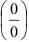, можно применить правило Лопиталя:
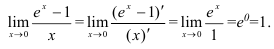
Ответ: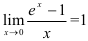 
.
Пример 5.
Вычислите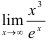 
.
Решение:
Поскольку в примере рассматривается неопределенность вида 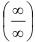, можно применить правило Лопиталя:
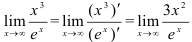. Снова получили неопределенность вида 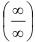, следовательно, можно применить правило Лопиталя еще раз:
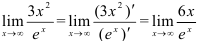. Повторно применяя правило Лопиталя, получим
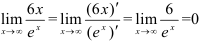, т.к. 
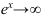при .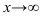
Ответ: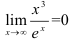 
.
Пример 6.
Вычислите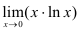 
.
Решение:
Поскольку при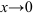 
функция 
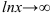, то имеет место неопределенность вида 
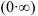и правило Лопиталя применить нельзя. Попытаемся преобразовать выражение, стоящее под знаком предела: 
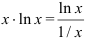. Тогда под знаком предела будет неопределенность вида 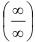, к которой правило Лопиталя применимо:
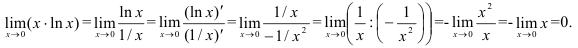
Ответ: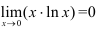 
.
На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:
Готовые контрольные работы по высшей математике
Обратите внимание на похожие контрольные работы возможно они вам будут полезны:
