Оглавление:
Прямая на плоскости. Кривые второго порядка
Задание: Составление уравнений прямых.
Цель: формирование умения составлять уравнения прямых на плоскости.
Задание для самостоятельной внеаудиторной работы:
7.1. Опираясь на обобщающие таблицы, изучите, какими способами можно задать прямую, и какие виды уравнения прямой существуют.
7.2. В треугольнике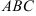 
заданы координаты вершин 
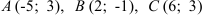. Составьте уравнение:
а) прямой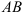 
;
б) медианы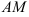 
;
в) прямой, проходящей через точку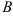 
параллельно 
;
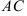г) прямой, проходящей через точку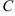 
с угловым коэффициентом 
.
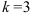7.3.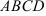 
— трапеция с основаниями 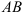и 
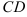, в которой 
.
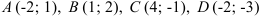Составьте уравнение:
а) диагонали 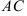в каноническом виде;
б) прямой, параллельной основаниям, проходящей через точку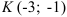 
в параметрическом виде;
в) прямой, проходящей через точку 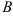и образующей с положительным направлением оси 
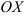угол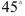 
(вид уравнения прямой — с угловым коэффициентом);
г) средней линии трапеции в каноническом виде;
д) прямой, проходящей через точку 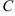параллельно прямой 
.
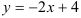7.4. Запишите уравнение прямой во всех видах (общем, каноническом, параметрическом, с угловым коэффициентом) и постройте эту прямую:
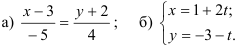
Методические указания по выполнению работы:
Уравнением линии на плоскости называется уравнение с двумя переменными 
и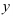 
, которому удовлетворяют координаты любой точки, лежащей на линии, и не удовлетворяют координаты любой точки, не лежащей на этой линии.
Прямые — самые простые линии на плоскости. Им соответствуют уравнения первой степени.
При решении задач удобно использовать следующие обобщающие таблицы:
Способы задания прямой
Виды уравнений прямой
Рассмотрим примеры решения типовых задач.
Пример 1.
Составьте уравнение прямой, проходящей через точку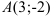 
и имеющей направляющий вектор 
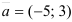в каноническом и параметрическом виде.
Решение:
Определим способ задания прямой: с помощью точки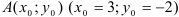 
и направляющего вектора 
.
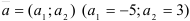Подставим координаты точки и направляющего вектора в уравнение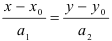 
: 
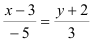— канонический вид.
Подставим координаты точки и направляющего вектора в уравнение
: 
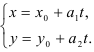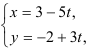— параметрический вид.
Ответ: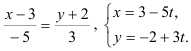 
Пример 2.
Составьте уравнение прямой, проходящей через точк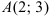и 
и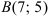 
.
Решение:
Подставив в формулу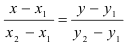 
координаты данных точек, получим искомое уравнение прямой: 
.
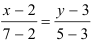Ответ: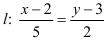 
.
Пример 3.
Составьте уравнение прямой, проходящей через точку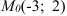 
и образующей с положительным направлением оси 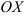угол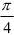 
.
Решение:
Найдём угловой коэффициент прямой: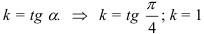 
.
Подставим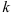 
и координаты точки 
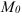в уравнение 
:
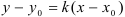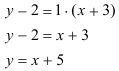
Ответ: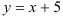 
.
На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:
Готовые контрольные работы по высшей математике
Обратите внимание на похожие контрольные работы возможно они вам будут полезны:
