Норма матрицы
Проблема собственных значений определена только для квадратных матриц. В экономической практике часто необходимо оценивать не только квадратные матрицы. Для такой оценки можно использовать универсальное понятие нормы, справедливое для матриц любой размерности.
Нормой произвольной матрицы 
называется действительное число 
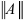, удовлетворяющее целому ряду условий, наиболее важными из которых являются:
1. 
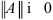, причем 
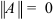только в случае полностью нулевой матрицы .
2. 
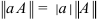, где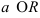 
.
В какой-то степени норму 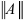можно образно представлять как показатель “толщины” или “мощности” матрицы .
Норма называется канонической, если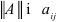 
, т.е. она не меньше, по модулю, любого элемента матрицы . При выборе нормы возможно использовать самые разнообразные соображения, не противоречащие определению. Однако на практике обычно достаточно следующих канонических норм:
1. 
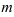-норма 
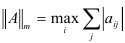— суммируются, по модулю, все строки матрицы и максимальная из полученных сумм объявляется нормой.
2. 
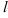-норма 
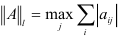— суммируются, по модулю, все столбцы матрицы и максимальная из полученных сумм объявляется нормой.
3. 
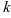-норма 
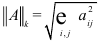— суммируются квадраты всех элементов матрицы и корень из этой суммы объявляется нормой.
Остальные темы находится на этой странице и там же можно заказать любые работы по высшей математике:
Обратите внимание на эти страниц, возможно они вам будут полезны:
| Систематическое интегрирование |
| Изгибы функции и их определение |
| Варианты уравнения прямой |
| Построение прямых. Расстояния |
