Изгибы функции и их определение
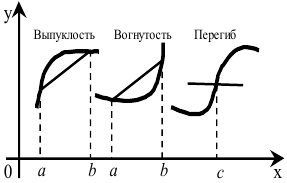
В целом ряде практически важных случаев анализа деталей процессов необходимо более подробно описывать изменяемость функции 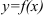 на интервале:
на интервале:
Назовем функцию 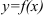 выпуклой вверх (или просто — выпуклой) на интервале
выпуклой вверх (или просто — выпуклой) на интервале 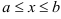 , если значения функции на этом интервале находятся выше отрезка, соединяющего точки
, если значения функции на этом интервале находятся выше отрезка, соединяющего точки 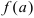 и
и 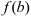 и вогнутой (или выпуклой вниз), если ее значения находятся ниже такого отрезка. Точку
и вогнутой (или выпуклой вниз), если ее значения находятся ниже такого отрезка. Точку 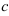 , в которой выпуклость сменяется вогнутостью (или наоборот) назовем точкой перегиба функции
, в которой выпуклость сменяется вогнутостью (или наоборот) назовем точкой перегиба функции 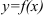 .
.
Выпуклость, вогнутость и точки перегиба определяются и анализируются с помощью второй производной по следующим правилам:
- Если значения второй производной
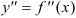 на интервале
на интервале 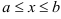 отрицательны, то функция
отрицательны, то функция 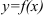 выпукла на этом интервале.
выпукла на этом интервале. - Если значения второй производной
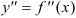 на интервале
на интервале 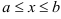 положительны, то функция
положительны, то функция 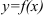 вогнута на этом интервале.
вогнута на этом интервале. - Необходимым условием для точки перегиба является то, что в ней вторая производная
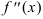 либо равна нулю, либо бесконечна, либо не существует. Если
либо равна нулю, либо бесконечна, либо не существует. Если 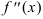 при переходе через эту точку меняет знак, то это — достаточное условие перегиба.
при переходе через эту точку меняет знак, то это — достаточное условие перегиба.
Таким образом, для исследования функции 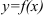 на изгибы и точки перегиба, можно использовать следующую схему:
на изгибы и точки перегиба, можно использовать следующую схему:
- Определяем производную
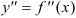 .
. - Находим стационарные точки из анализа области определения второй производной и решения уравнения
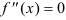 .
. - Определяем знаки второй производной
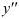 в интервалах между вычисленными точками и устанавливаем наличие точек перегиба и типы изгиба функции.
в интервалах между вычисленными точками и устанавливаем наличие точек перегиба и типы изгиба функции.
Остальные темы находится на этой странице и там же можно заказать любые работы по высшей математике:
Обратите внимание на эти страниц, возможно они вам будут полезны:
| Уравнения первого порядка с разделяющимися переменными |
| Систематическое интегрирование |
| Норма матрицы |
| Варианты уравнения прямой |

