Абсолютные экстремумы функции двух переменных
Как и в случае одной переменной, функция 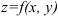 имеет узловые, определяющие структуру графика точки. В первую очередь это точки экстремума — минимума и максимума.
имеет узловые, определяющие структуру графика точки. В первую очередь это точки экстремума — минимума и максимума.
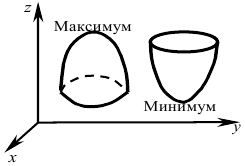
Функция 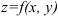 имеет максимум (минимум) в точке
имеет максимум (минимум) в точке 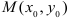 , если в любой, близкой к ней точке
, если в любой, близкой к ней точке 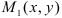 значения функции
значения функции 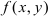 меньше (больше) значения
меньше (больше) значения 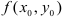 .
.
Процедура отыскания экстремумов функции 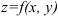 во многом подобна задаче для функции одной переменной. Сформулируем необходимое условие экстремума: если функция
во многом подобна задаче для функции одной переменной. Сформулируем необходимое условие экстремума: если функция 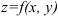 имеет экстремум в точке
имеет экстремум в точке 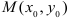 , то в этой точке ее первые частные производные равны нулю.
, то в этой точке ее первые частные производные равны нулю.
Таким образом, возможные точки экстремума (или стационарные точки) определятся из системы уравнений:
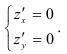
Так же, как и в случае функции одной переменной, если в области определения первых производных имеются точки, где производные равны бесконечности (или не существуют), то их следует включить в состав стационарных точек. Необходимое условие экстремума можно переформулировать также следующим образом: в точке минимума или максимума дифференцируемой функции градиент равен нулю.
Для определения фактического наличия экстремума и его типа необходимо применить достаточное условие. Аналог первого достаточного условия экстремума (по изменению знака производных при переходе через стационарную точку) на практике используется редко, из-за громоздкости вычислений и недостаточной наглядности. В связи с этим обычно используется аналог второго достаточного условия, который формулируется следующим образом:
Пусть функция 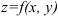 определена в некоторой окрестности стационарной точки
определена в некоторой окрестности стационарной точки 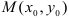 и имеет в этой точке непрерывные частные производные второго порядка
и имеет в этой точке непрерывные частные производные второго порядка
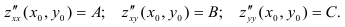
Здесь 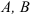 и
и 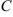 — константы. Тогда:
— константы. Тогда:
- если
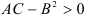 , то в точке
, то в точке 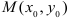 функция
функция 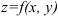 имеет экстремум, причем при
имеет экстремум, причем при 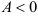 — максимум, при
— максимум, при 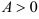 — минимум;
— минимум; - если
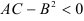 , то в точке
, то в точке 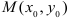 функция
функция 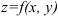 экстремума не имеет;
экстремума не имеет; - если
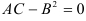 , то в точке
, то в точке 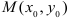 вопрос об экстремуме остается открытым и требуется дополнительное исследование — графическое или с применением первых частных производных (аналог первого достаточного условия).
вопрос об экстремуме остается открытым и требуется дополнительное исследование — графическое или с применением первых частных производных (аналог первого достаточного условия).
Исследование функции двух переменных на экстремум рекомендуется проводить по следующей схеме:
- Найти частные производные
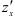 и
и 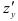 функции
функции 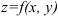 .
. - Найти стационарные точки функции.
- Найти частные производные второго порядка, вычислить их значения в каждой стационарной точке и с помощью достаточного условия сделать вывод о наличии экстремумов.
- Вычислить экстремумы (экстремальные значения) функции:
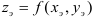 .
.
Заметим, что в стационарных точках, в которых исследование устанавливает отсутствие экстремума или оставляет вопрос открытым, может действительно не быть экстремума, но вполне может быть и случай, показанный на рисунке:
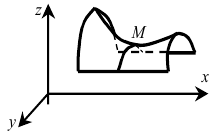
В точке 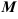 по одному направлению функция имеет минимальное значение, по перпендикулярному к нему направлению — максимальное. Такие точки называются седловыми или точками минимакса. Седловые точки являются двумерными аналогами точек перегиба функций одной переменной.
по одному направлению функция имеет минимальное значение, по перпендикулярному к нему направлению — максимальное. Такие точки называются седловыми или точками минимакса. Седловые точки являются двумерными аналогами точек перегиба функций одной переменной.
Кроме того, отметим, что, так же как и в случае функции одной переменной, если 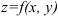 задается в ограниченной области
задается в ограниченной области 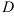 , можно ставить задачу об отыскании глобальных экстремумов. После определения всех локальных экстремумов по вышеизложенной схеме, необходимо вычислить значения функции на границе заданной области. Сравнение локальных экстремумов и граничных значений и позволяет найти наибольшее и наименьшее значения функции
, можно ставить задачу об отыскании глобальных экстремумов. После определения всех локальных экстремумов по вышеизложенной схеме, необходимо вычислить значения функции на границе заданной области. Сравнение локальных экстремумов и граничных значений и позволяет найти наибольшее и наименьшее значения функции 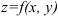 в заданной области
в заданной области 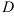 , т.е. глобальные экстремумы.
, т.е. глобальные экстремумы.
Остальные темы находится на этой странице и там же можно заказать любые работы по высшей математике:
Обратите внимание на эти страниц, возможно они вам будут полезны:
| Градиент функции двух переменных |
| Частные производные и дифференциалы |
| Варианты уравнения прямой |
| Построение прямых. Расстояния |

