Устанавливать сходимость или расходимость ряда в некоторых случаях позволяют свойства рядов. Рассмотрим основные свойства рядов.
Свойство 1. Если к ряду 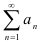 прибавить (или отбросить) конечное число членов, то полученный ряд сходится или расходится одновременно с данным.
прибавить (или отбросить) конечное число членов, то полученный ряд сходится или расходится одновременно с данным.
Свойство 2. Если ряд 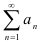 сходится, и его сумма равна
сходится, и его сумма равна 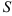 , то для произвольного числа
, то для произвольного числа 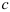 ряд
ряд
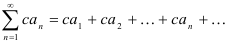
также сходится, и его сумма равна 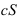 . Если же ряд
. Если же ряд 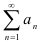 расходится и
расходится и 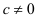 , то и ряд
, то и ряд 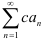 расходится.
расходится.
Свойство 3. Если ряды 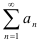 и
и 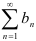 сходятся, и их суммы равны
сходятся, и их суммы равны 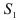 и
и 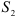 соответственно, то сходятся и ряды
соответственно, то сходятся и ряды 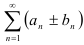 , причем сумма каждого равна соответственно
, причем сумма каждого равна соответственно 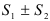 . Другими словами: сходящиеся ряды можно почленно складывать и вычитать. Из свойства 3 вытекают два следствия.
. Другими словами: сходящиеся ряды можно почленно складывать и вычитать. Из свойства 3 вытекают два следствия.
Следствие 3.1. Сумма (разность) сходящегося и расходящегося рядов есть расходящийся ряд. Следствие 3.2. Сумма (разность) двух расходящихся рядов может быть как сходящимся, так и расходящимся рядом.
Рассмотрим примеры использования свойств рядов при установлении их сходимости или расходимости.
Пример решения заказа контрольной работы №93.
Известно, что ряд 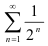 — сходится, а ряд
— сходится, а ряд  расходится. Применяя свойства рядов, исследуйте на сходимость ряды:
расходится. Применяя свойства рядов, исследуйте на сходимость ряды:
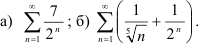
Решение:
а) Поскольку данный ряд 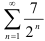 получается из сходящегося ряда
получается из сходящегося ряда 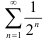 умножением на число
умножением на число 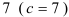 , следовательно, по свойству числовых рядов (свойство 2), он сходится.
, следовательно, по свойству числовых рядов (свойство 2), он сходится.
б) Поскольку данный ряд 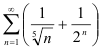 представляет собой сумму сходящегося
представляет собой сумму сходящегося 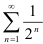 и расходящегося
и расходящегося 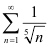 ряда, значит, по следствию из свойства рядов (следствие З.1.), он расходится.
ряда, значит, по следствию из свойства рядов (следствие З.1.), он расходится.
Ответ: а) 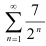 сходится; б)
сходится; б) 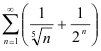 расходится.
расходится.
На этой странице вы сможете заказать контрольную работу и познакомиться с теорией и другими примерами решения:
Заказать контрольную работу по высшей математике
Другие похожие примеры возможно вам будут полезны:

