Метод Эйлера

Пусть необходимо решить дифференциальное уравнение вида 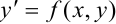при заданных начальных условиях ( 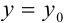при 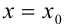) на отрезк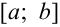е , где 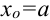. С помощью метода Эйлера мы сможем построить таблицу значений искомой функции 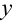на отрезке 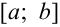вида:

Выполним следующие действия:

1. С помощью точек 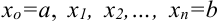разобьём отрезок 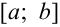на 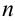равных частей длиной .

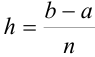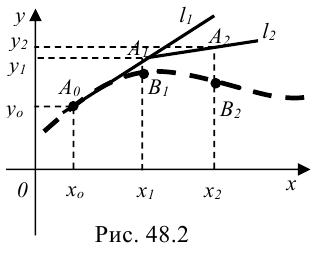
2. Попытаемся искомую интегральную кривую приближенно заменить касательными, проведенными в крайней левой точке каждого отрезка 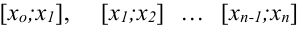(рис. 48.2) —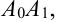

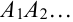
Уравнение касательной, проведенной к графику функции 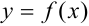в точке 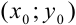, имеет вид: .

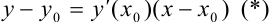3. Рассмотрим первый отрезок 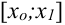. Касательная 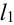, которую мы проводим к графику искомой функции в точке 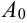, должна пройти через известную точку 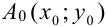и через некоторую точку
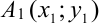, абсцисса которой — известное значение 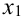, а ордината 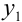неизвестна.

Поскольку точк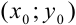и и 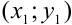лежат на касательной 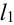, их координаты удовлетворяют уравнению касательной (*): .

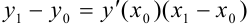По условию исходное дифференциальное уравнение имеет вид 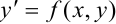, отсюда .

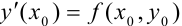Подставим 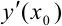в уравнение касательной .

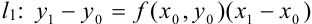Длина отрезк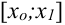а равна 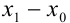или 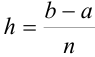, следовательно, уравнение касательной 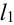примет вид: .

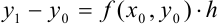Выразим из этого уравнения неизвестную переменную .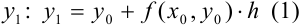

С помощью формулы (1) мы нашли ординату точки 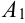, лежащей на касательной 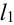. Если выбирать длину отрезка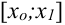 по-возможности небольшой, то ордината точки 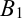, лежащей на искомой интегральной кривой и имеющей ту же абсциссу 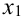, будет мало чем отличаться от найденного значения .

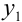4. Рассмотрим отрезок 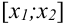. Координаты точки 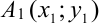нам известны, необходимо найти ординату 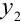точки 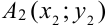. Проведя ту же цепочку рассуждений, что и в пункте 3, найдем формулу для расчета .

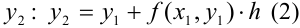Полученное число 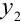будем считать приближенным значением искомой функции в точке .

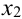Формулу (2) в общем виде можно записать следующим образом: 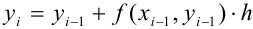, где 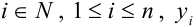— значения искомой функции в точках 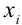. Для удобства все найденные значения 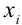и 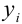заносят в таблицу.

Пример №48.1.

Дано дифференциальное уравнение 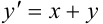. Найдите методом Эйлера на отрезке [0; 1] с шагом 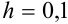численное решение задачи Коши с начальным условием .

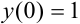Решение:

Заданное дифференциальное уравнение 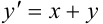соответствует виду дифференциальных уравнений 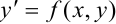, для которых применим метод Эйлера. В нашем случае .

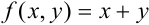Для удобства вычислений все расчеты будем выполнять в электронных таблицах Microsoft Excel. В качестве шапки таблицы можно предложить следующий вариант:

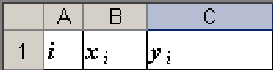
В столбце 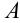будет указываться номер выполняемого шага: .

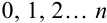В столбце 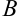будут располагаться значения 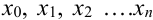. Поскольку 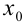— начало отрезка [0;1], то в ячейку 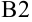занесем значение 0. Чтобы найти значение 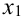, которое будет находиться в ячейке 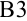, достаточно к началу промежутка 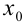прибавить ширину шага 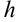. В ячейке 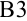будет находиться число 0 + 0,1 = 0,1. Для нахождения каждого последующего значения 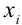к предыдущему необходимо прибавлять ширину шага до тех пор, пока 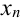не будет равно концу отрезка (числу 1).

В столбце 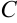будут содержаться значения искомой функции в точках 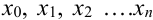. Значение 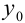берем из условия задачи Коши: 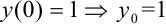. Заносим это число в ячейку 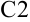. Чтобы
получить значение 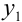, в ячейку 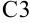достаточно ввести формулу, аналогичную формуле (1). В нашем примере она будет иметь вид: 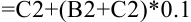. Для заполнения столбца оставшихся значений 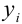можно воспользоваться возможностями автозаполнения. Тогда расчетная таблица будет иметь вид:

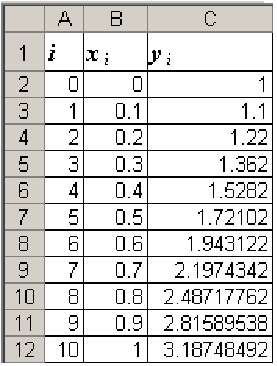
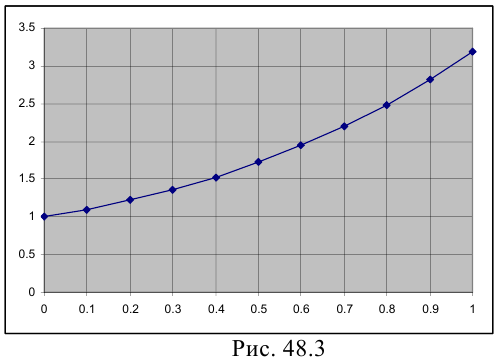
Данная таблица как раз и представляет собой численное решение задачи Коши методом Эйлера. Пользуясь этой таблицей можно построить на отрезке [0;1] искомую интегральную кривую, проходящую через точку (0; 1) (рис 48.3).

Подведем итог. Метод Эйлера задает простой алгоритм вычислений, но определяет табличные значения 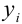с небольшой степенью точности. Это связано с тем, что касательная проводится в левом конце каждого рассматриваемого отрезка, и не учитывается поведение интегральной кривой на всем отрезке. По этой причине приближения 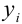оказываются достаточно грубыми, причем расхождения 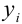с истинными значениями искомой функции растут к концу таблицы.

Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:

Предмет высшая математика

Другие лекции по высшей математике, возможно вам пригодятся:

Формула парабол (Симпсона).

Задача численного решения дифференциальных уравнений.

Понятие матрицы.

Виды квадратных матриц.