Напомним, что дифференциальным называется уравнение, содержащее производную или дифференциал искомой функции, например, 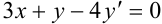 . Подчеркнем, что решением дифференциального уравнения является не число, а функция. Причем дифференциальное уравнение имеет множество решений, которые можно изобразить в виде семейства интегральных кривых.
. Подчеркнем, что решением дифференциального уравнения является не число, а функция. Причем дифференциальное уравнение имеет множество решений, которые можно изобразить в виде семейства интегральных кривых.
В практике чаше всего приходится иметь дело с задачей Коши: найти решение дифференциального уравнения при заданных начальных условиях (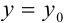 при
при 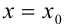 ). Геометрически это означает, что нужно выделить отдельную интегральную кривую, проходящую через точку
). Геометрически это означает, что нужно выделить отдельную интегральную кривую, проходящую через точку 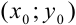 .
.
Потребность в приближенном решении задачи Коши возникает прежде всего в том случае, если дифференциальное уравнение нс принадлежит ни к одному из классов дифференциальных уравнений, для которых известны точные методы решения. Приближенные методы часто применяют и тогда, когда точные методы оказываются неэффективными, приводят к очень сложным расчетам и интегралам.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Формула трапеций. |
| Формула парабол (Симпсона). |
| Метод Эйлера. |
| Понятие матрицы. |
