Пусть задана функция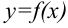 
, непрерывная на промежутке 
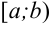. Пусть 
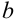— точка разрыва второго рода. Если существует конечный предел 
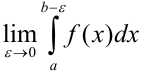, то его называют несобственным интегралом второго рода и обозначают 
.
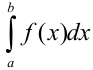Таким образом, по определению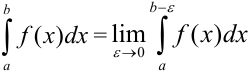 
.
Если найденный предел равен конечному числу, то говорят, что несобственный интеграл сходится. Если указанный предел не существует или бесконечен, то говорят, что интеграл расходится.
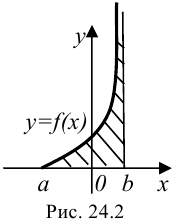
Геометрический смысл несобственного интеграла II рода
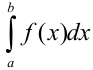, где 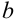— точка разрыва второго рода, 
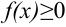, заключается в следующем: если 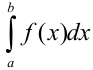сходится, то он представляет собой площадь «бесконечно высокой» криволинейной трапеции (рис. 24.2).
Аналогично вводится понятие несобственного интеграла II рода для
непрерывной на промежутке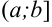 
функции при условии, что 
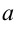— точка разрыва второго рода: 
.
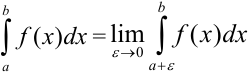Пример №24.3.
Вычислите несобственный интеграл II рода: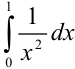 
.
Решение:
Подынтегральная функция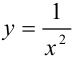 
непрерывна на промежутке (0;1], причем 
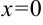— точка разрыва второго рода (
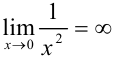). Для вычисления несобственного интеграла воспользуемся формулой: 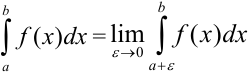. Получим, что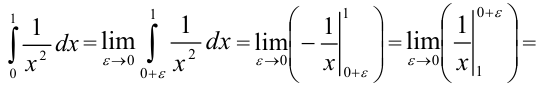 
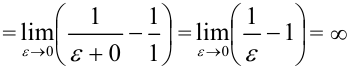. Видим, что несобственный интеграл II рода расходится.
Ответ: 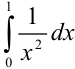расходится.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Понятие несобственного интеграла |
| Несобственные интегралы I рода. |
| Задачи, приводящие к понятию функции нескольких переменных. |
| Понятие функции двух действительных переменных. |
