Простым и удобным методом вычисления определенного интеграла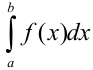 
от непрерывной функции является формула Ньютона-Лейбница: 
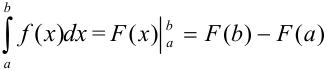. Этот метод применяется во всех случаях, когда может быть найдена первообразная 
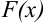для подынтегральной функции 
.
Пример №22.1.
Вычислите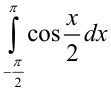 
.
Решение:
Сначала найдем неопределенный интеграл от заданной функции как интеграл от некоторой сложной функции, добавив границы интегрирования: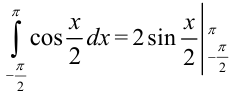 
.
Подставим сначала верхнюю, потом нижнюю границы интегрирования:
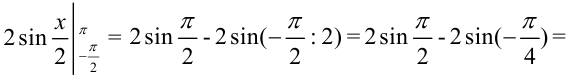
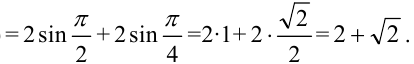
Ответ: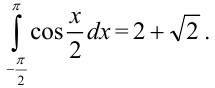 
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Основные свойства определенного интеграла. |
| Формула Ньютона-Лейбница. |
| Интегрирование подстановкой (заменой переменной). |
| Интегрирование по частям. |
