Оглавление:
Приведём без доказательства следующие теоремы о пределах функции.
Теорема 1. Функцию 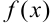 , стоящую под знаком предела
, стоящую под знаком предела 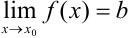 , можно представить в виде:
, можно представить в виде: 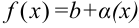 , где
, где 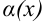 — бесконечно малая функция при
— бесконечно малая функция при 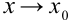 (т.е.
(т.е. 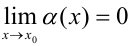 ).
).
Теорема 2 (о пределах суммы, произведения и частного). Если функции 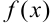 и
и 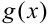 определены в некоторой окрестности точки
определены в некоторой окрестности точки  и существуют пределы
и существуют пределы 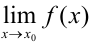 ,
, 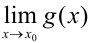 , то существуют пределы их суммы
, то существуют пределы их суммы 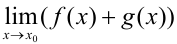 , произведения
, произведения 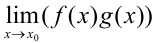 и, если
и, если 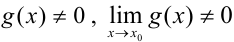 , то и частного
, то и частного 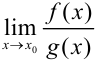 и имеют место равенства:
и имеют место равенства:
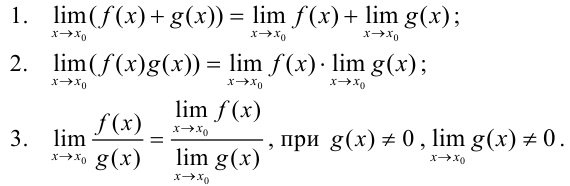
Отметим некоторые следствия из теоремы 2.
- Постоянный множитель может быть вынесен из-под знака предела.
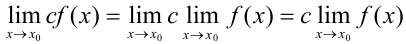 (поскольку
(поскольку 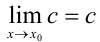 );
); - Предел разности равен разности пределов.
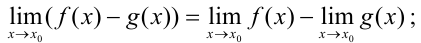
- Предел степени равен степени предела.
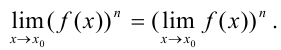
Рассмотрим, как данные теоремы применяются при нахождении предела функции в точке.
Пример №9.1.
Вычислите: 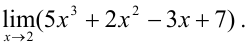
Решение:
Используя теорему 2.1 и следствие 2, получаем, что предел суммы и разности равен сумме и разности соответствующих пределов:
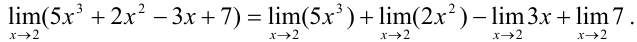
В силу следствия 1, постоянный множитель может быть вынесен за знак предела:
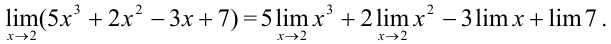
В силу следствия 3, предел степени равен степени предела:
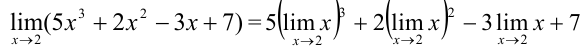
По определению 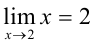 , следовательно,
, следовательно,
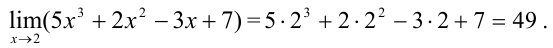
Ответ: 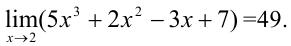
Таким образом, для вычисления предела многочлена при 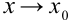 достаточно вместо переменной
достаточно вместо переменной  подставить значение
подставить значение  и выполнить соответствующие действия, т.е.
и выполнить соответствующие действия, т.е. 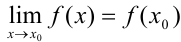 .
.
Пример №9.2.
Вычислите: 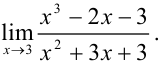
Решение:
Чтобы применить теорему 2.3 о пределе частного 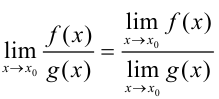 , проверим выполнение следующих условий:
, проверим выполнение следующих условий: 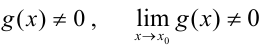 . Поскольку
. Поскольку 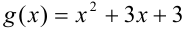 , найдем
, найдем 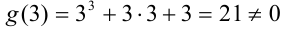 и предел многочлена
и предел многочлена 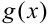 :
: 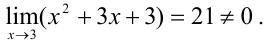
Применим теорему 2.3: 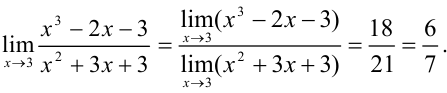
Ответ: 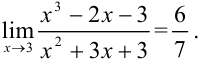
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Понятие предела функции. |
| Односторонние пределы. |
| Техника вычисления пределов. |
| Предел функции на бесконечности. |

