Уравнение Бернулли для элементарной струйки идеальной жидкости

Уравнение Бернулли для элементарной струйки идеальной жидкости

Уравнение Бернулли для элементарной струйки идеальной жидкости. Рассматривая стационарное течение идеальной жидкости только под действием силы тяжести, в этом случае мы выводим основные уравнения, связанные с давлением жидкости и ее скоростью. Возьмите 1 из элементарных потоков, составляющих поток, и выберите участки 1 и 2 любой длины для этого потока (рис.1.22).Сделайте площадь первого участка равной скорости d311 C 37 Давление px и высота центра тяжести поперечного сечения, которая отсчитывается от любой горизонтальной плоскости G сравнения 2-го сечения, соответственно e82, g\, p2 и За бесконечно короткий промежуток времени<11 выбранный участок потока перемещается в положение V2′.

Схема вывода уравнения Бернулли Участок тарана имеет знак минус, так как направление силы диаметрально противоположно направлению движения. Людмила Фирмаль

• Применим теорему механики к массе жидкости в объеме сечения струйки, что работа силы, передаваемой телу, равна кинетической анергии этой жидкости. body. In в данном случае такой силой является давление, которое нормально действует на поверхность Пожалуйста, опубликуйте ручеек и серьезность проблемы. Рассчитаем работу давления, силы тяжести и изменение кинетической энергии сечения струйки за время t1. Работа давления в первом сечении положительна, так как направление силы совпадает с направлением движения и выражается как произведение силы pxi3 и пути b \ <11\. Рисунок 1.22. и определяется по формуле. РХ&8х б \ ■■п%<!8 <1и.

Давление, действующее со стороны сегмента струйки, не действует, так как оно перпендикулярно этой поверхности и, следовательно, перпендикулярно движению. Таким образом, действие давления будет равным P1P1 \ Д8 P2P2 <18г Д1>(1.43） Поскольку работа силы тяжести равна изменению потенциальной энергии положения сечения струйки, необходимо вычесть энергию положения жидкости в объеме V-2 ’из энергии положения жидкости в объеме 1-2.In в этом случае позиционная энергия промежуточного продукта 1 ’-2 уменьшается, и остается только разность энергий между элементами 1-G, 2-24.Рассматривая уравнение течения (1.41), нетрудно заметить гравитацию объема, а значит и штрихованного элемента 1 -. V и 2-2 ′ равны друг другу： 99 = p ^©8111 ^ p $ъ%©8%11.

• Работа силы тяжести выражается как произведение разности высот силы тяжести. Восемьдесят восемь <Для расчета приращения кинетической энергии рассматриваемого потока в течение 12 часов кинетическую энергию объема 1 необходимо вычесть из кинетической энергии объема 1-2.При вычитании кинетическая энергия промежуточного продукта V-2 уменьшается, сохраняется только разница в кинетической энергии элементов 2-2 ’и 1-1′, а сила тяжести каждого из них равна<10.Поэтому приращение кинетической энергии различно (1.46） Если работа давления сложить вместе, то потребуется усилие в 1 см.

Уравнение (1.43) 1 гравитационная работа[опорное уравнение (1.45)]и равна этой сумме приращению кинетической энергии[опорное уравнение (1.46）]、 Р1 <%5 ^ \ <&-Р * <11(ГХ-АА) н0 = * 1)G0 и /(2§). (1.46’)） Разделите это уравнение на<1C[опорное уравнение (1.44) 1, и уменьшите、 ± Р^ РГ РЖ РЖ Б П * Как вы это делаете? г ^ 2 * 9 (1.47). Группируйте термины, относящиеся к первому разделу левого раздела, уравнения правого раздела и термины, относящиеся ко второму разделу. Где r-геометрическая высота, или геометрическое давление. p / (p#) *высота манометра, или манометр; g ’ 2 /(2^)-скоростная высота, или скоростной шшор. Выведен в 173B Даниэлем Бернулли. Форма слоговой* ％ Это называется полным давлением. Б-4 ^ П В * ■ / г I = sopz1 (вдоль струйки).

Полученное уравнение называется уравнением Бернулли идеального элементарного потока несжимаемой жидкости. Людмила Фирмаль

• Уравнение Бернулли (1.47)описывается для 2 секций произвольно приобретенных струек и представляет собой равенство и в полной статье в этих разделах. Сечение получается произвольно, поэтому для других участков того же потока максимальное давление будет иметь одинаковое значение. * Д. Бернулли (1700-1782) швейцарский студент, сын выдающегося математика Иоганна Бернулли, жил в России с 1725 по 1733 год и был пленником Петербургской Академии наук. С 1733 года-профессор Университета г. Basel. In его работа, Механика жидкости выделила много гидравлических проблем, в том числе вывод выше equations. As паук, он считается одним из основателей гидравлики.、 Восемьдесят девять.

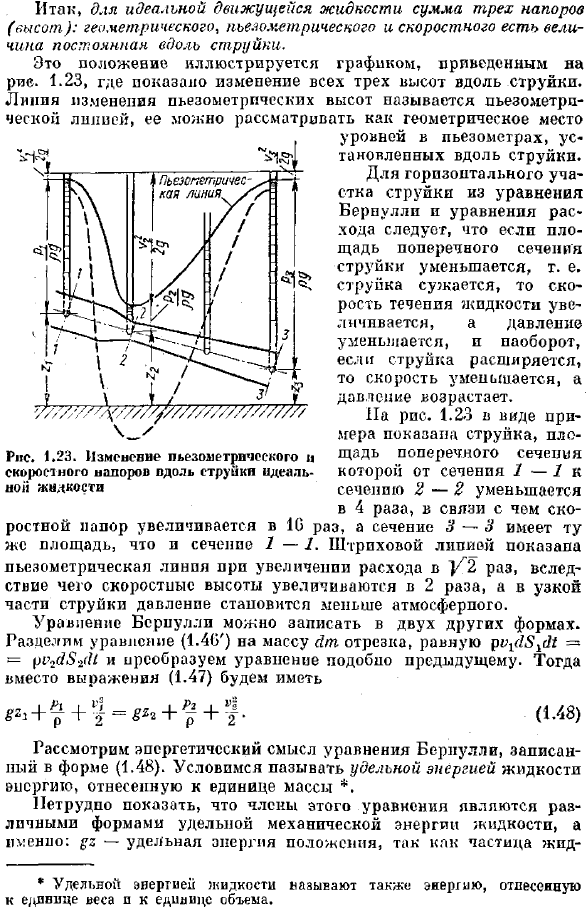
Таким образом, для идеальной движущейся жидкости в общей сложности 3 головки (высота): геометрическая, пьезометрическая и скорость постоянны вдоль струйки. Это положение показано на графике, приведенном на рисунке. 1.23 показывает все 3 изменения высоты вдоль струйки. Линия пьезометрического изменения высоты называется пьезометрической Лилией и может рассматриваться как геометрическое место Уровень пьезоэлектрического измерителя устанавливается вдоль струйки. В горизонтальном сечении струйки, из уравнения Бернулли и уравнений течения, если площадь поперечная.

Смотрите также:

Методические указания по гидравлике

Возможно эти страницы вам будут полезны:

1. Кинематика и динамика жидкости.
2. Расход. Уравнение расхода.
3. Вывод дифференциальных уравнений движения, идеальной жидкости и их интегрирование.
4. Уравнение Бернулли для потока реальной (вязкой) жидкости.