Оглавление:




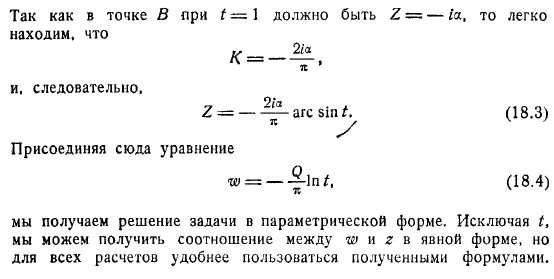








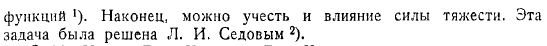

Метод Жуковского — Митчеля. Истечение из отверстия. Удар струи в пластинку. Глиссирующая пластинка.
Планк Н. Е. Жуковский и Митчелл предложили модификацию Кирхгофа в гидромеханике состоит в замене функции на функцию и нахождении конформного отображения плоскости разреза на ту часть плоскости, которая соответствует области течения в плоскости.Если обтекаемый контур состоит из отрезков прямой линии, то поиск ранее упомянутой карты может быть осуществлен с помощью известного метода Шварца-кристфеля formula.In в этом случае, поскольку прямые линии X и Y соответствуют границам режимов течения плоскости в plane.
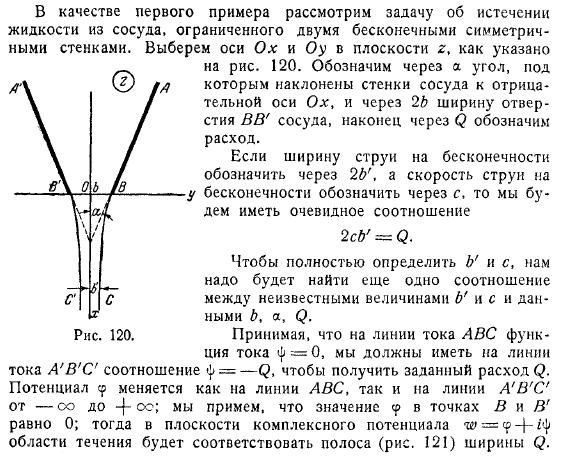
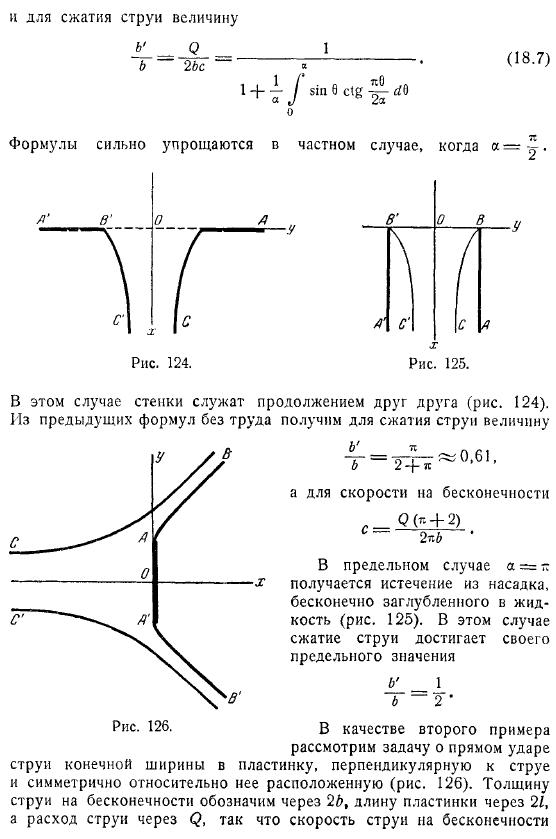
Факт, я записал его с осторожностью, что K a получается, следуя границе потока φ0 плоскости x вдоль плоской стенки. получает xn.As в качестве первого примера рассмотрим задачу вытекания жидкости из контейнера, окруженного 2 бесконечными симметричными стенками Кирхгоффа. Выберите оси Ox и Oy в плоскости, как показано на рисунке.
- Стенки сосуда наклонены относительно отрицательной оси Ox, выраженной в виде угла через ширину отверстия в взрывчатом сосуде, И, наконец, скорости потока.Если мы обозначим ширину струи на Бесконечности через C, а скорость струи на Бесконечности через c, то это очевидная зависимость. чтобы полностью определить b и c, вам нужно найти другую связь между неизвестными величинами b и c и данными.
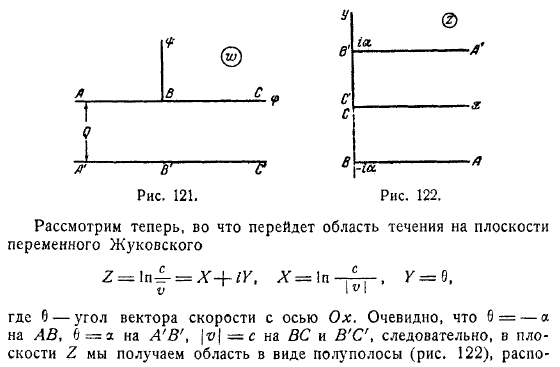
Предполагая, что у вас есть текущая функция f на линии потока, вам нужно соотношение f на линии потока ABC, чтобы получить данный поток.Потенциал с изменяется от ω до os как на линии, так и на линии ABC.Предполагая, что значения в точках B и B равны, область течения соответствует полосе на рисунке в плоскости комплексного потенциала P cff.Ширина. поскольку c является очевидным, он расположен на правой стороне Оси O y.
To получив конформное отображение этой полоски на полосу на плоскости, введем еще одну вспомогательную плоскость и предположим, что верхняя полуплоскость этой плоскости соответствует области обтекания фигуры. Как известно, если задано соответствие 3 точек контура, то такое конформное отображение полностью determined.So вы принимаете, что точка C переходит в точку O, точка B переходит в точку, а точка A переходит в точку. В этом случае, в зависимости от симметрии, точка B переместится в эту точку, но вы можете легко определить зависимость.
Сначала найдите функцию.За то, что figure.As соответствующий комплексный потенциал, пришло время рассматривать плоскость как плоскость мнимого потока, поэтому ясно, что все линии тока должны двигаться из точки А в точку С, и количество жидкости, поступающей в точку С из верхней полуплоскости, равно.Но если вы представите, что точка С имеет раковину силы, а других особенностей больше нет, то вы должны получить именно такую flow.So мы можем принять это…И любая константа исчезнет.
Однако вы можете непосредственно подтвердить, что эта функция отображает верхнюю полуплоскость на полосу переменного тока плоскости.Чтобы найти функцию, нужно найти конформное отображение полуполосы плоскости на плоскость верхней половины.Рассмотрим эту полосу как треугольник с одной из его вершин, удаленной бесконечно, и сопоставим ее с верхней полуплоскостью вспомогательной комплексной переменной по Шварцу-Кристофелю formula.As известно, что форма последнего выражения-r L.
Как туда попасть и это помогает отобразить конформную внутренность плоскости определенным углом с внутренним углом а, причем верхняя половина плоскости по отношению к периметру многоугольника соответствует всей реальной оси point…To функция. содержит n чисел, не зависящих от n вещественных параметров. из n числа I, an, геометрий относятся к известным зависимостям nn r, а каждая из комплексных констант A и B имеет 2 параметра.
- Поскольку формы и положения многоугольника полностью определяются путем установки Н-координата вершины, Шварца-Кристоффеля формула позволяет указать любые 3 параметра,
- Идеально соответствуют друг другу, например, полное определение конформного отображения при установлении соответствия 3 контурных точек, что соответствует тому, что было сказано выше.В этом случае вершина треугольника ШПД имеет угол, и вершин Б, Б соответствуют плоскости точки ко.
Но если я oe, формула Шварца Кристоффеля принимает форму U. примените ее к нашему случаю и обратите внимание, что она представляет собой O, r.получите CPosition осей. Людмила Фирмаль
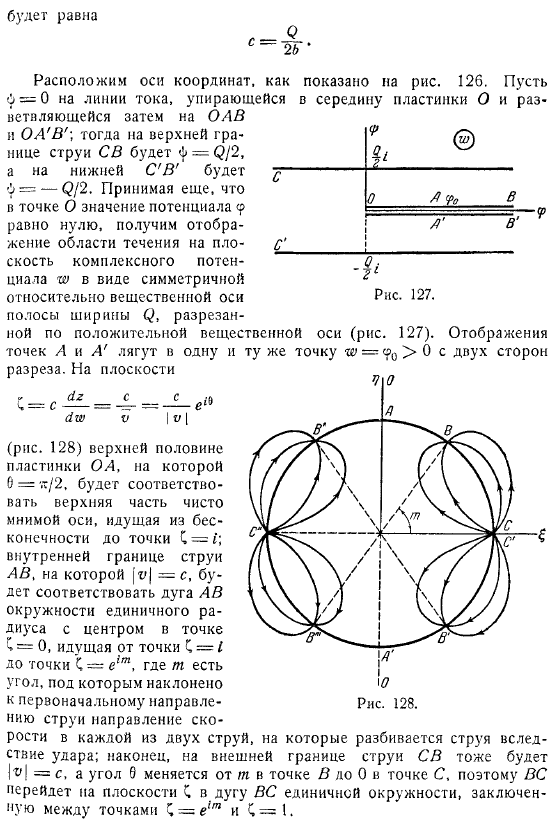
Затем поместите его на линию потока, поместите OAB на верхнюю границу струи, поместите CB и поместите его на нижний CB.А если предположить, что в точке О значение потенциала Р равно нулю, то получим отображение области течения в плоскость комплексного потенциала в виде симметричной зависимости.
Отображение точек A и A находится в одной и той же точке с обеих сторон разреза.На плоскости рисунка верхней половины пластины помещается О. Т. К.Соответствует вершине чистой мнимой оси и достигает внутренней границы струи AB от Бесконечности к точке C, на которой c соответствует дуге AB единичного радиуса с центром (перемещаясь из точки C в точку C).Где m-угол наклона в исходном направлении.
- Направление скорости каждой из 2-х струй, в которых струя разделена столкновением, в конечном итоге есть также c на внешней границе струи C, и угол изменяется от m точки B до точки C, так что самолет движется к плоскости C, показанной на рисунке C дуги окружности, окруженной точками et и C блока BC. Когда вы запускаете O и эти аргументы в середине пластины, легко увидеть, что область потока проходит по плоскости C, вытягивая полукруг, ограниченный LAN VA из правой полуплоскости.
Чтобы найти взаимное конформное отображение 2 областей, полученных плоскостью и C, представьте, что плоскость C представляет собой воображаемую плоскость потока в течение некоторого времени.Этот поток может быть complex.As вы можете видеть, все линии потока выполняются. Если мы проведем эти линии на плоскости C, то в воображаемом потоке мы можем заключить, что точка C представляет собой источник, а точки B и B-Сток.
Для того, чтобы линия была линией потока, она должна быть расположена симметрично на точках B и B, на точках B и B, на стоках той же интенсивности, что и точки B и C, и на точках C, которые являются источниками того же самого Метод Леви-Чивита выглядит как точка C. Далее, вы получите схему течения, показанную на рисунке 5. Очевидно, что в точках C и C только половина этого потока достигает начальной области потока, которая ограничена линией OABSVAO от точки C, поэтому нам нужно разместить сильный источник.Точно так же в точках B, B, B необходимо разместить приемник интенсивности. Легко построить сложные возможности. Из источника и стока получается т. к.
- Тогда вы можете написать C. Следовательно, formula.It может быть представлена в следующем виде: используется при исследовании газовых струй.
- Другой 1 находится справа, другой 1-плоскость, перпендикулярная пластине и пересекающая струйку.
- Разница между количеством движения, которое проходит через левую плоскость с течением времени, и количеством движения, которое проходит через правую плоскость за то же время, становится apparent.
- To для этого нам нужно добавить приращение импульса за счет потока в струйке.
Горизонтальная проекция этой величины будет равна p. если P-давление пластины, то горизонтальная проекция импульса силы времени c выглядит так:так возникает сопротивление. Если мы умножим эту формулу, мы получим подъем P p. Очевидно, что гидродинамический момент относительно задней кромки пластины будет равен M. Здесь p-давление на пластину, которое определяется с помощью интеграла Бернулли.
Интеграл не так прост, как другие интегралы в этом разделе.Однако это также может быть точно рассчитано, только конечный результат p P M получается. Картина распределения давления на фигурной пластине получена с использованием интеграла Бернулли и формулы.И..То же самое будет выбрано везде, см. рисунок.Где p. распределение давления egi хорошо согласуется с экспериментом.
При небольшом угле атаки игнорируйте его с помощью прямоугольного кронштейна. получаем меньший срок по сравнению с п. Калининым Н. момент давления, действующего на строгальную плиту, ученные записки СГУ, т. к. Серия PMI, vol. и… И Н.,, Вы можете сделать следующее: и … Конечно, o-это небольшое количество 2 степени.От.И так далее on.It следует за его сопротивлением и подъемной силой.
Момент для задней кромки равен моменту LL эти формулы показывают, что подъемная сила строгальной доски равна половине подъемной силы при малом угле атаки.Людмила Фирмаль
Смотрите формулу, то есть крыло плоское,а точка действия подъемной силы строгальной доски, как и крыло, расположена на некотором расстоянии от задней кромки. И так далее on.In наша проблема, мы предположили, что жидкость бесконечна.Задача о скольжении с учетом дна решается с помощью эллипса

