Помощь по статистике — решение заданий и задач онлайн

Здравствуйте! Я Людмила Анатольевна Фирмаль, занимаюсь помощью студентам более 17 лет. У меня своя команда грамотных, сильных преподавателей. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И неважно – она по объёму на две формулы или огромная, сложно структурированная, на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте.

Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!

Как получить помощь в выполнении заданий по статистике

Вы можете написать сообщение в WhatsApp. После этого я оценю ваш заказ и укажу стоимость и срок выполнения вашей работы. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за вашу работу, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл готовой работы в личные сообщения.

Сколько стоит помощь

Стоимость помощи зависит от задания и требований Вашего учебного заведения. На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости, загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.

Какой срок выполнения

Минимальный срок выполнения составляет 2-4 дня, но помните, срочные задания оцениваются дороже.

Как оплатить

Сначала пришлите задание, я оценю, после вышлю вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.

Гарантии и исправление ошибок

В течение 1 года с момента получения Вами готового решения действует гарантия. В течении 1 года я и моя команда исправим любые ошибки.

Чуть ниже я предоставила теорию она поможет освежить знания и примеры оформления заказов по некоторым темам статистики, так я буду оформлять ваши работы если закажите у меня, это не все темы, это лишь маленькая часть их, чтобы вы понимали насколько подробно я оформляю.

Введение в статистику

Понятие об исследовании количественных сторон объектов и явлений начало формироваться с момента развития у человека элементарных навыков работы с информацией. Уже в древнем мире появилась потребность подсчитывать численность жителей государства, учитывать людей, пригодных к военному делу, определять количество скота, размеры земельных угодий и другого имущества. Информация такого рода была необходима для сбора налогов, ведения войн и т.п. В дальнейшем, по мере развития общественной жизни, круг учитываемых явлений постепенно расширяется.

Особенно возрастает объем собираемой информации с развитием капитализма и международных экономических связей. Потребности этого периода вынуждали органы государственного управления и капиталистические предприятия собирать для практических нужд обширную и разнообразную информацию о рынках труда и сбыта товаров, сырьевых ресурсах.

В середине XVII в. в Англии возникло научное направление, получившее название «политической арифметики», начало которому положили Уильям Петти (1623—1687) и Джон Граунт (1620—1674 гг.). Его теоретики на основе изучения информации о массовых общественных явлениях стремились открыть закономерности общественной жизни и таким образом ответить на вопросы, возникавшие в связи с развитием капитализма.

Наряду со школой «политических арифметиков» в Англии, в Германии развивалась школа описательной статистики, или «государствоведения». Возникновение этой науки относится к 1660г.

Развитие политической арифметики и государствоведения привело к появлению науки статистики.

Понятие «статистика» происходит от латинского слова «status», которое в переводе означает положение, состояние, порядок явлений.

В научный оборот термин «статистика» ввел профессор Геттингенского университета Готфрид Ахенваль (1719—1772).

Возможно эта страница вам будет полезна:

Предмет статистики

В зависимости от объекта изучения статистика как наука подразделяется на:

• социальную,
• демографическую,
• экономическую,
• промышленную,
• торговую,
• банковскую,
• финансовую,
• медицинскую и т.д.

Общие свойства статистических данных, независимо от их природы, и методы их анализа рассматриваются математической статистикой и общей теорией статистики.

Статистикой называют отрасль знаний, обладающую своим предметом и методом.

Термин «статистика» может означать данные или иначе говоря, результаты многих наблюдений и измерений (например – статистика забастовок, целодневных простоев, успеваемости в школе, вузе, колледже и т.д.). Статистика может быть определена как собирание, представление, анализ и интерпретация числовых данных.

Таким образом, под статистикой понимается практическая деятельность по сбору, накоплению, обработке и анализу цифровых данных, характерезующих население, экономику, культуру, образование и другие явления в жизни общества.

Предмет статистики

Предметом статистического изучения выступают совокупности – множество однокачественных, варьирующих явлений, их три основные категории:

• это множество явлений (например – колледж);
• это множество явлений, объединенных общим качеством, представляющих собой проявления одной и той же закономерности (например – группа студентов);
• это множество варьирующих явлений, отличающихся по своим характеристикам (например – каждый студент).

Современную статистику в рассматриваемом смысле этого слова отличает от «государствоведения» прошлых столетий не только значительно выросшая полнота и разносторонность содержащихся в ней сведении. В отношении характера сведений к ней теперь относят только то, что получает количественное выражение. Например, количественные данные о численности населения, пользующегося тем или иным языком в качестве своего разговорного, количественные данные о распределении населения, промышленности по регионам, и т.д.

Общая черта сведений, составляющих статистику, — они всегда относятся не к одному единичному (индивидуальному) явлению, а охватывают сводными характеристиками целый ряд таких явлений, или, как говорят, их совокупность. Индивидуальное явление отличается от совокупности своей неразложимостью на самостоятельно существующие и аналогичные друг другу составные элементы. Совокупность же состоит именно из таких элементов. Исчезновение одного из элементов совокупности не уничтожает ее как таковую.

Таким образом, статистика имеет дело, прежде всею, с количественной стороной явлений и процессов общественной жизни. Одной из характерных особенностей статистики является то, что при изучении количественной стороны общественных явлений и процессов она всегда отображает качественные особенности исследуемых явлений, т.е. изучает количество в неразрывной связи, единстве с качеством.

Статистика — это наука, изучающая количественную сторону массовых общественных явлений в неразрывной связи с их качественной стороной, количественное выражение закономерностей общественного развития.

В статистических измерениях используются – стоимостные (цены), натуральные (литры, метры ит.д.), трудовые (человеко-часы, человеко-дни) и условно-натуральные измерители (консервы в условных банках, скот- пересчитывают в крупный рогатый скот и.д.).

Теоретической основой предмета статистики являются положения социально-экономической теории и принципы диалектического метода познания.

Методы статистики 

Для изучения своего предмета статистика разрабатывает и применяет разнообразные методы, совокупность которых образует статистическую методологию. Применение в статистическом исследовании конкретны методов предопределяется поставленными при этом задачами и зависит от характера исходной информации.

Основной метод статистики — диалектический метод познания всех явлений в их взаимозависимости и взаимообусловленности.

К специфическим методам статистики относят:

1)статистическое наблюдение;
2)сводку и группировку полученных данных;
3)статистический анализ.

В случае необходимости статистическое исследование может содержать дополнительный этап — статистический прогноз.

Статистическое наблюдение — научно организованный сбор данных о явлениях и процессах общественной жизни посредством регистрации по заранее разработанной программе наблюдения их существенных признаков. Данные наблюдения представляют собой первичную статистическую информацию о наблюдаемых объектах, которая является основой для получения их обобщающих характеристик. Наблюдение — один из главных методов статистики и одна из важнейших стадий статистического исследования.

Сводка — процесс приведения в систему полученных данных, их обработка и подсчет промежуточных и общих итогов, расчет взаимосвязанных величин аналитического характера. Понятие сводки включает в себя действия по группировке статистических данных.

Статистический анализ — исследование характерных особенностей структуры, связи явлений, тенденций, закономерностей развития социально-экономических явлений, для чего используются специфические экономико-статистические и математико-статистические методы. Статистический анализ завершается интерпретаций полученных результатов.

Статистический прогноз — научное выявление состояния и вероятных путей развития явлений и процессов, основанное на системе установленных причинно-следственных связей и закономерностей.

Основные категории и понятия статистики 

Основные категории и понятия статистики:

Статистическая совокупность — множество варьирующих объектов, явлений, объединенных какими-либо общими свойствами и подвергающихся статистическому исследованию (например, совокупность промышленных предприятий региона, совокупность лиц, рожденных в 1991 г., и т.д.). Каждый элемент статистической совокупности называется единицей совокупности.

Отличительная черта, свойство, качества, присущие единице совокупности и учитываемые при статистическом исследовании, называются признаком.

Признаки человека – возраст, образование, род занятия, рост, вес.
Признаки предприятия – форма собственности, специализация (отрасль), численность работников, величина уставного капитала (фонда), уровень деятельности.

В статистическом анализе признаки подразделяются по характеру влияния друг на друга.

Признак-результат — признак, анализируемый в данном исследовании. Рассматривается как следствие взаимодействия других факторов.
Признак-фактор — признак, оказывающий влияние на исследуемый признак (признак-результат). Зависимость между признаком-фактором и признакомрезультатом может быть количественно определенна. Синонимами данного термина в статистике являются «факторный признак», «фактор».
Признак-вес — такой признак, который необходимо учесть при расчетах. Но признак-вес не оказывает влияния на исследуемый признак.

Изменение величины признака в статистической совокупности, т.е. наличие у единиц совокупности разных значений признака, являющееся следствием воздействия на элементы совокупности множества различных причин (факторов), называется вариацией.

Собранные в ходе статистического наблюдения и подвергнутые первичной обработке данные представляют собой ряд распределения. Если ряд распределения построен по количественному признаку, то такой ряд называется вариационным.

Исследование изменений общественных явлений, выраженных с количественной стороны и определенных в качестве предмета статистической науки, производится с помощью статистических показателей.

Индивидуальные показатели — показатели, характеризующие исследуемый процесс по одной единице совокупности.
Сводные показатели — показатели, характеризующие общественное явление по группе исследуемых единиц (делятся на объемные и расчетные).
Сводные объемные показатели — показатели, получаемые путем сложения значений признака каждой единицы совокупности. Величина, образуемая при исчислении данного показателя, называется объемом признака.

Расчетные сводные показатели — показатели, которые рассчитываются с помощью специальных формул и математических методов и применяются для анализа сложных общественных явлений.
Плановые показатели — показатели, величина которых отражает уровень изучаемого явления, который должен быть достигнут в соответствии с планом.
Отчетные показатели — показатели, величина которых отражает уровень изучаемого явления, достигнутый в исследуемом периоде (если признак моментный) или за исследуемый период (если признак интервальный).
Базисные показатели — показатели, величина которых при нимается в качестве базы для сравнения.
Прямые показатели — показатели, которые непосредственно характеризуют изучаемое свойство. Как правило, упоминаются вместе с обратными показателями, являющимися в математическом смысле обратными величинами для прямых показателей.
Абсолютные показатели — показатели, отражающие свойства явления, выраженные первичными признаками. Такие показатели являются результатом первичного учета и выражаются в абсолютных величинах.
Относительные показатели — показатели, получающиеся путем соотнесения абсолютных показателей. Выделяют несколько видов относительных показателей. В результате расчета относительных показателей получаются коэффициенты, единицы измерения и др.
Средние показатели — показатели, характеризующие величину изучаемого признака, приходящуюся на единицу совокупности. Получаются путем соотнесения сводных объемных (определяющих) показателей, выражающих исследуемый признак, с числом единиц совокупности, обладающих этим признаком.
Величина — количественная характеристика размеров социально-экономических явлений, их соотношения, степени изменения, взаимосвязи. Величины делятся на абсолютные, относительные и средние.
Единица измерения — значение, в котором выражается и с которым сравнивается исследуемая величина. Единицы измерения статистического показателя определяются его содержанием (например, число родившихся младенцев, рассчитанное на каждую тысячу жителей региона, будет измеряться в промилле, которое обозначается как «%о»).
Период — момент или интервал времени, являющийся составной частью структуры статистического показателя. Применение понятия «период» в статистике обусловлено расчетом относительных показателей, когда помимо множества факторов, влияющих на изменение общественного явления, учитывается также фактор времени. В статистике выделяют несколько видов периодов:
базисный период — период времени, со значением которого сравнивается значение другого периода (отчетного, см. ниже). Значение показателя, принятого за основу для сравнения, называют также «базисной величиной»; отчетный период имеет два значения:

а) период времени, значение которого сравнивается со значением другого периода, базисного. Сравниваемое значение показателя называют еще «отчетной величиной»;
б) период времени, по истечении которого представляется очередная статистическая отчетность.

Задачи статистики 

Одной из главных задач статистики является изучение на основе статистических данных происходящих в стране социально-экономических и научнотехнических процессов и явлений, экономический анализ материалов и представление Президенту, Правительству, федеральным органам исполнительной власти официальной статистической информации по актуальным вопросам экономического и социального развития страны, выполнения государственных и региональных программ по решению важнейших народнохозяйственных проблем.

Отраслевое деление статистической науки, сформированное к настоящему времени, позволяет выделить следующие задачи статистики:

• совершенствование методики статистического наблюдения в связи со все более широким применением выборочного наблюдения;
• приведение системы статистических показателей в соответствие с современными международными рекомендациями для стран с рыночной экономикой;
• расширение аналитических возможностей системы статистических показателей;
• определение роли субъективных и объективных факторов в социальной сфере;
• исследование взаимовлияния всех составляющих развития общества друг на друга;
• обеспечение доступности статистических данных с целью расширения круга их пользователей.

Место статистики среди других экономических и общественных наук

Место статистики в системе наук определяется ее органичной связью с научными дисциплинами, изучающими основные закономерности и качественные особенности в той или иной области знаний. С одной стороны, статистика опирается на общие положения экономической теории, на требования экономических законов производства, распределения, обмена и потребления материальных благ. С другой стороны, она имеет самое непосредственное отношение к выявлению количественной стороны средств производства, предметов труда в их сочетании с совокупной рабочей силой общества, и т.п.

Современная статистика кроме общетеоретического содержания включает в себя серию отраслевых статистик и комплексных разделов этих статистик.

В соответствии с принятой в Российской Федерации классификацией наук различают следующие составные части статистики:

• общая теория, в которой излагаются ее общие принципы и методы;
• экономическая статистика, изучающая систему показателей народного хозяйства, его структуру, пропорции, взаимосвязи отраслей и элементов общественного воспроизводства;
• отраслевые статистики — промышленная, сельскохозяйственная, строительства, транспорта, связи, демографическая, труда и др., задачей которых является изучение системы показателей, анализ социально-экономических процессов соответствующих отраслей народного хозяйства. Формируются другие направления статистических исследований и статистических наук, особенно это касается множества вновь возникающих экономических структур рыночной экономики. Сюда в первую очередь следует включить статистику рынка труда, рынка капиталов и т.п.

Организация государственной статистики в РФ и международной статистики

Организация статистики в РФ

Статистика играет важную роль в управлении экономическим и социальным развитием страны, так как правильность любого управленческого решения во многом зависит от той информации, на основе которой оно принято. Только точные, достоверные и правильно проанализированные данные должны приниматься во внимание на высоких уровнях управления.

Изучением экономического и социального развития страны, отдельных регионов, отраслей, фирм, предприятий занимаются специально созданные для этого органы, образующие статистическую службу. В Российской Федерации функции статистической службы выполняют органы государственной статистики и органы ведомственной статистики.

Предоставление статистической информации – главная задача органов государственной и ведомственной статистики, информация является продукцией их деятельности.

Высшим органом управления статистикой в нашей стране является Федеральная служба государственной статистики (ФСГС), созданная в соответствии с Указом Президента РФ от 09.03.2004 № 314 «Структура федеральных органов исполнительной власти». ФСГС является федеральным органом исполнительной власти, осуществляющим функции по формированию официальной статистической информации о социальном, экономическом, демографическом и экологическом положении страны, а также функции по контролю и надзору в области государственной статистической деятельности на территории РФ.

Федеральная служба государственной статистики находится в ведении Министерства экономического развития и торговли РФ.

Согласно постановлению Правительства РФ от 07.04.2004 № 188 основными функциями Федеральной службы государственной статистики являются:

• представление в установленном порядке статистической информации Президенту РФ, Правительству РФ, Федеральному Собранию РФ, органам государственной власти, средствам массовой информации, организациям и гражданам, а также международным организациям;
• разработка и совершенствование научно обоснованной официальной статистической методологии для проведения статистических наблюдений и формирования статистических показателей, обеспечение соответствия указанной методологии международным стандартам;
• разработка и совершенствование системы статистических показателей, характеризующих состояние экономики и социальной сферы;
• сбор статистической отчетности и формирование на ее основе официальной статистической информации;
• контроль за выполнением организациями и гражданами, осуществляющими предпринимательскую деятельность без образования юридического лица, законодательства РФ в области государственной статистики;
• развитие информационной системы государственной статистики, обеспечение ее совместимости и взаимодействия с другими государственными информационными системами;
• обеспечение хранения государственных информационных ресурсов и защиты конфиденциальной и отнесенной к государственной тайне статистической информации;
• реализация обязательств РФ, вытекающих из членства в международных организациях и участия в международных договорах, осуществление международного сотрудничества в области статистики.

Методология статистических показателей, формы и методы сбора и обработки статистических данных, установленные ФСГС, являются официальными статистическими стандартами РФ.

В своей основной деятельности ФСГС руководствуется федеральными статистическими программами, которые формируются с учетом предложений федеральных органов исполнительной и законодательной власти, органов государственной власти субъектов РФ, научных и других организаций и утверждаются ФСГС по согласованию с Правительством РФ.

Основной задачей статистических органов страны является обеспечение гласности и доступности общей (не индивидуальной) информации, а также гарантия достоверности, точности и правдивости учтенных данных. Кроме того, задачами ФСГС являются:

• представление официальной статистической информации Президенту РФ, Правительству РФ, Федеральному Собранию РФ, федеральным органам исполнительной власти, общественности, а также международным организациям;
• координация статистической деятельности федеральных органов исполнительной власти и органов исполнительной власти субъектов РФ, обеспечение условий для использования указанными органами официальных статистических стандартов при проведении ими отраслевых (ведомственных) статистических наблюдений;
• разработка экономико-статистической информации, ее анализ, составление национальных счетов, необходимых балансовых расчетов;
• гарантирование полноты и научной обоснованности всей официальной статистической информации;
• предоставление всем пользователям равного доступа к открытой статистической информации путем распространения официальных докладов о социально-экономическом положении Российской Федерации, субъектов РФ, отраслей и секторов экономики, публикации статистических сборников и других статистических материалов.

В результате реформирования экономики РФ изменилась и структура органов статистики. Местные районные статистические регистратуры упразднены и образованы межрайонные отделы статистики, которые являются представительствами территориальных органов статистики. Организация статистических органов России сейчас находится на стадии реформирования. На рис. 1 представлена схема органов статистики РФ с 2004 г.

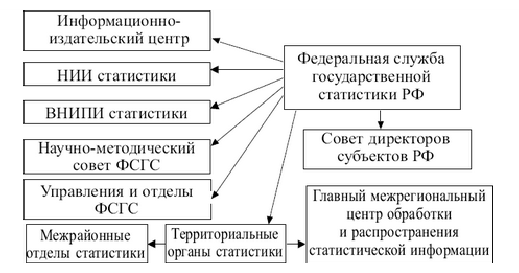
Рис. 1. Схема органов статистики Российской Федерации с 2004 г.

Наряду с государственными статистическими службами существует ведомственная статистика, которая ведется в министерствах, ведомствах, на предприятиях, в объединениях и фирмах различных отраслей экономики. Ведомственная статистика занимается сбором, обработкой и анализом статистической информации, необходимой для руководства, принятия управленческих решений, планирования деятельности предприятия или органа власти. На небольших предприятиях этой работой, как правило, занимается либо главный бухгалтер, либо непосредственно сам руководитель. На крупных предприятиях с разветвленной собственной региональной структурой или большой численностью, на крупных производствах организуются целые отделы или управления, занимающиеся анализом статистической информации. К этой работе привлекаются специалисты в области статистики, математики, бухгалтерского учета и экономического анализа, менеджеры и технологи. Подобная «команда», вооруженная современными средствами вычислительной техники, опираясь на методологию, предлагаемую теорией статистики и используя современные методики анализа, помогает строить эффективные стратегии развития бизнеса, а также эффективно организовывать деятельность органов государственной власти. Управлять сложными социальными и экономическими системами, не располагая оперативной, полной и достоверной статистической информацией, невозможно.

Таким образом, перед органами государственной и ведомственной статистикой стоит очень важная задача теоретического обоснования объема и состава статистической информации, которая соответствовала бы современным условиям развития экономики, способствовала рационализации в системе учета и статистики и минимизированию затрат на выполнение этой функции.

Организация статистики в РФ 

Организация международной статистики осуществляется:

1. Статистическими службами ООН;

2. Специализированными учреждениями;
— Международная организация труда (МОТ);
— Продовольственная и сельскохозяйственная организация ООН (ФАО);
— Всемирная организация здравоохранения (ВОЗ);

3. Другими международными организациями:
— Организация экономического сотрудничества и развития (ОЭСР);
— Европейский союз (ЕС);
— Международный валютный фонд (МВФ);
— Мировой банк.

Деятельность статистических служб этих организаций включает:
— разработку международных стандартов, обеспечивающих сравнимость статистических показателей разных стран;
— осуществление международных сопоставлений;
— публикацию данных по группам, регионам и миру в целом.

Зарубежные национальные и международные статистические публикации можно подразделить на:

1. Сводные, включающие данные по всем разделам статистики (важнейший – ежегодник ООН Statistical Yearbook);

2. Специализированные, включающие данные по какой-либо одной отрасли (по финансовой, демографической, сельскохозяйственной и др. статистике).

Научным международным центром в области статистики является Международный статистический институт (ISI).

Координация деятельности статистических служб стран-членов СНГ осуществляется созданным в 1992 г. Статистическим Комитетом Содружества Независимых Государств.

Возможно эта страница вам будет полезна:

Примеры решения задач по статистике

Статистическое наблюдение

Понятие статистического наблюдения

Проведение статистического исследования невозможно без качественной информационной базы, получаемой в ходе статистического наблюдения. Поэтому с момента изменения представлений о статистике как о науке описательной, разрабатываются особые правила проведения наблюдения и специальные требования к его результатам — статистическим данным. То есть наблюдение является одним из основных методов статистики.

Статистическое наблюдение — это массовое, планомерное, научно организованное наблюдение за явлениями социальной и экономической жизни, которое заключается в регистрации отобранных признаков у каждой единицы совокупности.

Статистическое наблюдение выступает первым этапом статистического исследования, оно совпадает в основном с первой {чувственной или эмпирической) ступенью процесса познания общественной жизни, является важнейшим специфическим статистическим приемом исследования. Как и всякое исследование, оно начинается со сбора фактов, наблюдения; выводы, обобщения как в науке, так и в практике ценны лишь тогда, когда они основываются на фактах.

Статистическое наблюдение может проводиться:

• органами государственной статистики,
• научно-исследовательскими институтами,
• экономическими службами банков, бирж, фирм.

К статистическим данным, пригодным для обобщений, предъявляется ряд требований:

• данные должны быть максимально полными, не отрывочными, неслучайно выхваченными;
• данные должны быть абсолютно достоверными и точными;
• данные должны соответствовать принципу единообразия, сопоставимости;
• данные должны соответствовать принципу своевременности (сбор должен быть организован только в строго определенное время; данные должны быть представлены в срочном порядке).

Объект статистического наблюдения — это та совокупность, о которой должны быть собраны необходимые сведения (например, совокупность промышленных предприятий, фермерских хозяйств района и т.д.). Совокупность состоит из отдельных единиц.

Единицей наблюдения называют тот составной элемент объекта наблюдения, который является носителем признаков, подлежащих регистрации. В одном какомлибо наблюдении может быть не одна, а несколько единиц наблюдения. Так при переписи населения, например, единицей наблюдения может быть или человек (житель), или семья, или то и другое.

Единицы наблюдения, как и объект в целом, обладают, как правило, множеством различных признаков. Все их учесть невозможно, поэтому необходимо определить главные.

Перечень признаков (вопросов), регистрируемых в процессе наблюдения, называют программой статистического наблюдения. Точная и исчерпывающая формулировка вопросов программы необходима для того, чтобы обеспечить одинаковое их понимание всеми участвующими в наблюдении лицами. В этих целях часто в формулировку вопросов включается так называемый подсказ, т.е. варианты возможных ответов.

Процесс проведения статистического наблюдения включает следующие этапы:

• подготовка наблюдения;
• проведение массового сбора данных;
• подготовка данных к автоматизированной обработке;
• разработка предложений по совершенствованию статистического наблюдения.

Формы и виды наблюдения 

На этапе подготовки обследования нужно выяснить, как часто оно будет проводиться, будут ли обследоваться все единицы совокупности или только часть их, как получать информацию об объекте (путем интервью по телефону, по почте, простым наблюдением и т. п.). Другими словами, необходимо определить формы, способы и виды статистического наблюдения.

В отечественной статистике используются три организационные формы (типа) статистического наблюдения:

1.отчетность (предприятий, организаций, учреждений и т.п.);
2.специально организованное статистическое наблюдение (переписи, единовременные учеты, обследования сплошного и несплошного характера);
3.регистры.

Статистическая отчетность — это основная форма статистического наблюдения, с помощью которой статистические органы в определенные сроки получают от предприятий, учреждений и организаций необходимые данные в виде установленных в законном порядке отчетных документов, скрепляемых подписями лиц» ответственных за их представление и достоверность собираемых сведений. То есть отчетность — это официальный документ, содержащий статистические сведения о работе предприятия, учреждения, организации и т.п.

Действующую статистическую отчетность делят на типовую и специализированную. Состав показателей в типовой отчетности является единым для предприятий всех отраслей народного хозяйства. В специализированной отчетности состав показателей изменяется в зависимости от особенностей отдельных отраслей экономики.

По срокам представления отчетность бывает:

• — ежедневная,
• — недельная,
• — двухнедельная,
• — месячная,
• — квартальная,
• — годовая.

Кроме годовой отчетности все перечисленные виды представляют собой текущую отчетность.

Специально организованное наблюдение проводится с целью получения сведений, отсутствующих в отчетности, или для проверки ее данных. Примером такого наблюдения является перепись (населения, материальных ресурсом, многолетних насаждений, оборудования и др.) — специально организованное наблюдение, повторяющееся, как правило, через равные промежутки времени, с целью получения данных о численности, составе и состоянии объекта статистического наблюдения по ряду признаков.

Характерными особенностями переписи являются:

• одновременность проведения ее на всей территории, которая должна быть охвачена обследованием; единство программы наблюдения;
• регистрация всех единиц наблюдения по состоянию на один и тот же критический момент времени.

Программа наблюдения, приемы и способы получения данных по возможности должны оставаться неизменным. Это позволяет обеспечить сопоставимость собираемой информации и получаемых в ходе разработки материалов переписи обобщающих показателей. Тогда можно не только определить численность и состав исследуемой совокупности, но и проанализировать ее количественное изменение в период между двумя обследованиями.

Регистровое наблюдение — это форма непрерывного статистического наблюдения за долговременными процессами, имеющими фиксированное начало, стадию развития и фиксированный конец. Оно основано на ведении статистического регистра, который представляет собой систему, постоянно следящую за состоянием единицы наблюдения и оценивающую силу воздействия различных факторов на изучаемые показатели.

В регистре каждая единица наблюдения характеризуется совокупностью показателей. Одни из них остаются неизменными в течение всего времени наблюдения и регистрируются один раз; другие показатели, периодичность изменения которых неизвестна, обновляются по мере изменения; третьи — представляют собой динамические ряды показателей с заранее известным периодом обновления. Все показатели хранятся до полного завершения наблюдения за единицей обследуемой совокупности. В практике статистики различают:
— регистры населения;
— регистры предприятий.

По видам наблюдения делятся:
— по моменту наблюдения (текущее, периодическое, единовременное).
— по полноте охвата единиц совокупности (сплошное, несплошное); При текущем наблюдении изменения в отношении изучаемых явлений фиксируются по мере их наступления (например при регистрации рождений, смерти, состояния в браке). Такое наблюдение проводится с целью изучения динамики какоюлибо явления.

Данные, отражающие изменения объекта, могут быть собраны в ходе нескольких обследований. Они обычно проводятся по схожей программе и инструментарию и называются периодическими (переписи населения, которые проводятся через каждые 10 лет, регистрация цен производителей по отдельным товарам).

Единовременное обследование дает сведения о количественных характеристиках какого-либо явления или процесса в момент его исследования. Повторная регистрация проводится спустя какое-то время (не определенное заранее) или может не проводиться вообще (например, инвентаризация незавершенного производственного строительства 1990 г.).

Сплошное наблюдение — учет всех без исключения единиц в пределах данной совокупности (например, перепись всех видов оборудования или материалом на данном предприятии). Материалы сплошного наблюдения позволяют выделить в составе изучаемой массы единицы качественно однородной группы и определить по каждой группе средние величины по наиболее существенным признакам. Единовременное и текущее наблюдения осуществляются в форме сплошного наблюдения, если необходимо получить сведения об объеме изучаемых явлений.

Организация сплошного наблюдения не всегда возможна и целесообразна, особенно, для контроля за качеством продукции. В этом случае сплошное наблюдение приводит к исключению из сферы практического использования массы продукции предприятий. Поэтому необходимо осуществлять несплошное (частичное) наблюдение — учитывать только часть единиц совокупности, по которой составляют представление о характерных особенностях изучаемого явления в целом.

Существуют следующие виды несплошного наблюдения:

1.выборочное наблюдение — строится на принципах теории вероятностей и позволяет строго математически обрабатывать материалы: при исследовании только части единиц совокупности полученные результаты можно переносить на всю совокупность; монографическое обследование — тщательному обследованию подвергаются отдельные единицы изучаемой совокупности, обычно представители каких-либо новых типов явлений. Проводится с целью выявления имеющихся или намечающихся тенденций в развитии данного явления;

2.анкетное наблюдение — это вид несплошного наблюдения и одновременно — способ получения информации. Оно состоит в том, что разработанная анкета распространяется в определенном кругу лиц и после заполнения возвращается статистическим (или другим) органам. Заполнение анкеты — добровольное, возможна анонимность;

3.метод моментных наблюдении — информация собирается путем регистрации значений признаков у единиц выборочной совокупности в некоторые заранее определенные моменты времени. Поэтому метод моментных наблюдений предполагает отбор не только единиц исследуемой совокупности (выборку в пространстве), но и моментов времени, в которые проводится регистрация состояния исследуемого объекта (выборка во времени), применяется, например, при проведении обследований доходов населения;

4.метод основного массива — обследованию подвергаются самые существенные, обычно наиболее крупные единицы изучаемой совокупности, которые по основному (для конкретного исследования) признаку имеют наибольший удельный вес в совокупности (используется для организации наблюдения за работой городских рынков).

Возможно эта страница вам будет полезна:

Курсовая работа по статистике

Способы наблюдения 

Сплошное и несплошное статистическое наблюдение осуществляется различными способами:

• — непосредственным наблюдением,
• — опросом,
• — документированной записью.

Непосредственным называют такое наблюдение, при котором сами регистраторы путем непосредственного замера, взвешивания, подсчета или проверки работы и т.д. устанавливают факт, подлежащий регистрации, и на этом основании производят записи в формуляре наблюдения (например, изучение интенсивности пассажиропотоков на городском транспорте).

Документальный способ наблюдения основан на использовании в качестве источника статистической информации различного рода документов, как правило, учетного характера. При надлежащем контроле за постановкой первичного учета и правильном заполнении статистических формуляров документальный способ дает наиболее точные результаты.

Опрос — это способ наблюдения, при котором необходимые сведения получают со слов респондента. Он предполагает обращение к непосредственному носителю признаков, подлежащих регистрации во время наблюдения, и используется для получения информации о явлениях и процессах, не поддающихся непосредственному прямому наблюдению. Опрос осуществляют следующими способами:

• устный (используется в переписях населения, в социологических исследованиях);
• анкетный, или саморегистрация (используется при переписях бюджета семей, службами занятости; более точный, но и более дорогостоящий);
• корреспондентский (предполагает рассылку статистическими и другими органами управления специально разработанных бланков и инструкций по их заполнению хозяйствующим субъектам или специально выделенным лицам — корреспондентам для изучения определенного вопроса. Сведения поступают в установленные сроки по почте, телеграфом или доставляются нарочным. Способ не требует особых затрат, но качество информации зависит от уровня знаний и степени подготовки корреспондентов).

Ошибки наблюдения 

Точностью статистического наблюдения называют степень соответствия величины какого-либо показателя (значение какого-либо признака), определенной по материалам статистического наблюдения действительной его величине.

Расхождение между расчетным и действительным значением изучаемых величин называется ошибкой наблюдения.

При большом числе единиц исследуемой совокупности ошибки и неточности могут погашаться, но если применяется выборочное наблюдение, то ошибки могут существенно повлиять на результаты исследования.

В зависимости от причин возникновения различают:
— ошибки регистрации;
— ошибки репрезентативности.

Ошибки регистрации — отклонения значения показателя, полученного в ходе статистического наблюдения от фактического, действительного его значения. Возможны как при сплошном, так и при несплошном наблюдении. Ошибки регистрации делятся на случайные и систематические.

Случайные ошибки регистрации могут быть вызваны различными причинами (невниманием, усталостью, низкой квалификацией работника, и др.) и выражаются в пропусках, описках, внесении данных в не те графы таблицы. Они не влияют на результат исследования, ибо с помощью законов теории вероятностей их можно нивелировать.

Систематические ошибки регистрации имеют одинаковую тенденцию либо к увеличению, либо к уменьшению значения показателей по каждой единице наблюдения, и поэтому величина показателя по совокупности в целом будет включать в себя накопленную ошибку (например, округление возраста населения при проведении социологических опросов — многие опрашиваемые вместо 48-49 и 51-52 лет говорят, что им 50 лет).

Ошибка репрезентативности — это отклонение значения показателя обследованной совокупности от его величины по исходной совокупности. Такие ошибки характерны только для несплошного наблюдения. Возникают потому, что отобранная и обследованная совокупность недостаточно точно воспроизводит (репрезентирует) всю исходную совокупность в целом. Также бывают случайными и систематическими.

Случайные ошибки репрезентативности — ошибки, отражающие неравномерное распределение единиц в совокупности, в связи с чем выборочная совокупность некорректно характеризует генеральную совокупность.

Систематические ошибки репрезентативности появляются вследствие нарушения принципов отбора единиц из исходной совокупности, которые должны быть подвергнуты наблюдению.

Чтобы устранить обнаруженные ошибки в материалах статистического наблюдения, производится контроль собранных данных первичного учета, который осуществляется в двух направлениях:

— счетный, или арифметический контроль — заключается в проверке точности арифметических расчетов, применявшихся при составлении отчетности или заполнении формуляров статистического наблюдения;
— логический контроль — заключается в проверке ответов на вопросы программы наблюдения путем их логического осмысления или путем сравнения полученных данных с другими источниками по этому же вопросу.

Логический контроль осуществляется различными способами:

1)сравниваются ответы на различные вопросы одного итого же формуляра, например сопоставляются в бланке переписи населения сведения о профессии, возрасте, семейном положении;

2)сопоставляются записи, относящиеся к отчетному периоду, с аналогичными записями предшествующих периодом или же с плановыми данными отчетного периода:

3)сравниваются фактические данные статистического наблюдения с разработанными нормативами: затрат времени, удельного расхода материалов и др.;

4)сопоставляются данные проведенных статистических наблюдений с результатами специальных наблюдений выборочного характера, в силу своих особенностей позволяющих получить более полные данные по отобранной массе единиц.

Как правило, для исправления ошибок, выявленных в ходе логического контроля, требуется повторно обратиться к источнику сведений.

Сводка и группировка

Понятие сводки и группировки

Специфика предмета статистики – это специфика статистического метода, он включает:

• — сбор данных – статистическое наблюдение;
• — обобщение данных наблюдения (включает сводку и группировку);
• — представление данных в подходящей форме и компактно;
• — анализ и интерпретацию.

В результате первой стадии статистического исследования — статистического наблюдения — получают сведения о каждой единице совокупности. Задача второй стадии статистического исследования состоит в том, чтобы упорядочить и обобщить первичный материал, свести его в группы и на этой основе дать обобщенную характеристику совокупности. Этот этап в статистике называется сводкой.

Статистическая сводка — систематизация единичных фактов, позволяющая перейти к обобщающим показателям, относящимся ко всей изучаемой совокупности и ее частям, и осуществлять анализ и прогнозирование изучаемых явлений и процессов.

Различают:
— простую сводку (подсчет только общих итогов);
— статистическую группировку.

Статистическая группировка сводится к расчленению совокупности на группы по существенному для единиц совокупности признаку. Группировка позволяет получить такие результаты, по которым можно выявить состав совокупности, характерные черты и свойства типичных явлений, обнаружить закономерности и взаимосвязи. Группировка является основным методом обработки собранной информации.

Чтобы сгруппировать данные, необходимо ознакомиться со всеми результатами наблюдения и сделать первичные выводы о характеристиках изучаемого объекта. Именно поэтому группировку иногда называют первичным анализом данных.

Способ разработки статистической сводки может быть:
— централизованным;
— децентрализованным.

При централизованной сводке все данные сосредоточиваются в одном месте и сводятся по разработанной методике.

При децентрализованной сводке обобщение материала осуществляется снизу доверху по иерархической лестнице управления, подвергаясь на каждом из них соответствующей обработке.

Положив начало научной систематизации и обработке исходной информации, сводка и группировка статистических данных служат тем самым базой для осуществления всестороннего анализа и прогнозирования коммерческой деятельности на рынке товаров и услуг.

Виды группировок 

Выделяют несколько видов группировок, применение которых обусловлено характером единиц совокупности:

• типологическая группировка — подразделяет единицы в зависимости от их типа. Применяется, как правило, для группировок по атрибутивным (качественным) признакам. Отрицательной стороной является подверженность субъективным взглядам исследователя при отнесении единиц к различным типам явления;

• структурная группировка — характеризует структуру изучаемой совокупности, т.е. отвечает на вопросы:
— какие части можно выделить в объекте наблюдения,
— каково соотношение между ними (или какой удельный вес в целом имеет каждая часть).
Как правило, осуществляется по одному признаку;

• аналитическая группировка — характеризует степень влияния одного фактора объекта на другой. Причем влияющий фактор называют признак-фактор, а параметр, подверженный влиянию, — признак-результат.

Иногда учитывается несколько признаков-факторов, тогда такая группировка называется многомерной (многофакториой).

Образование групп по двум и более признакам, взятым в определенном сочетании, называется комбинированной группировкой. При этом группировочные признаки принято располагать, начиная с атрибутивного (качественного), в определенной последовательности, исходя и 1 логики взаимосвязи показателей. Применение комбинированных группировок обусловлено многообразием экополитических явлений, а также необходимостью их всестороннего изучения. Примером комбинированной группировки может служить разделение образованных групп по формам хозяйствования на подгруппы по уровню рентабельности или по другим признакам (производительность труда, фондоотдача и т.д.).

Особенностью аналитических группировок является тот факт, что группировка считается выполненной после применения элементов корреляционно-регрессионного анализа, т.е. после количественного определения меры зависимости между факторами.

Наиболее сложный вопрос теории группировок — выбор группировочного признака.

Группировочные признаки 

Социально-экономические явления отличаются большим многообразием форм своего развития, и поэтому при группировке встает вопрос о выборе того признака, который адекватен цели исследования и характеру исходной информации. Определяющими являются признаки, наиболее полно и точно характеризующие изучаемый объект, позволяющие выбрать его типичные черты и свойства.

Группированные признаки (или основание группировки) — это признаки, по которым производится распределение единиц наблюдаемой совокупности на группы. Так, при группировке населения по месту проживания выделяются две группы: городское и сельское население. Число возможных групп статистических данных может быть ограничено соответствующими признаками (атрибутами) такими как иол, возраст, образование, классовая принадлежность и т.п. Однако группировки могут формироваться по множеству других признаков и не только в статике на определенную дату, но и в динамике, т.е. на протяжении каких-то лет, взятых в определенном интервале.

Поскольку единицы совокупностей подвергаемых группировке, обладают многими признаками, то группы могут быть образованы по одному или нескольким признакам, взятым в определенной комбинации. Группировки по одному признаку называются простыми, группировки по двум и более признакам, взятым в сочетании с другим, называется комбинационными. Примером комбинационных группировок может быть таблица численности городского и сельского населения в нашей стране по данным переписи 1970 г. Указанные в таблице группировки населения по признаку «городское и сельское население» не только представлены в динамике, т.е. в процессе исторического развития страны с 1913 по 1970 г., но и раскрывают этот процесс в абсолютных и относительных числах.

По форме выражения группировочные признаки могут быть:
— атрибутивными (качественными);
— количественными (численными).

При этом количественные признаки, в свою очередь, могут быть:
— дискретными (прерывными), значения которых выражаются только целыми числами (число комнат в квартире, число человек в семье и т. д.),
— интервальными (непрерывными), принимающими как целые, так и дробные значения (рост человека, вес, зарплата, метраж квартиры, объем проданных населению товаров в стоимостном выражении, сумма издержек обращения).

Вопрос о числе групп и границах интервала для каждого вида группировок должен решаться по-разному, исходя из целей исследования, значения изучаемого признака, объема коммерческой деятельности и т.д.

Количество групп во многом зависит от того, какой признак служит основанием группировки. Так, нередко атрибутивные группировочные признаки предопределяют число групп. По аналогии также расчленяется совокупность по дискретному признаку, изменяющемуся в незначительном диапазоне.

Различают:
— открытые интервалы,
— закрытые интервалы.

Открытые интервалы имеют какую-нибудь одну обозначенную границу в первой и последней интервальной группе, а замкнутые — и верхнюю и нижнюю границы интервала.

Интервалы групп устанавливаются только при значительной колеблемости дискретного признака и при непрерывно изменяющемся количественном признаке (величина зарплаты).

Величина интервала — это разность между максимальными и минимальными значениями признака в каждой группе. Эту величину можно определить и как разность между верхними или нижними границами значений признака в смежных группах

Интервалы бывают:
— равные (построение замкнутых интервалов);
— неравные (построение открытых интервалов).

Величину интервала можно определить по формуле:

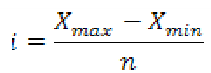
где i — величина интервала,
Xmax и Xmin — максимальное и минимальное значение признака в совокупности,
n— число групп.

Возможно эта страница вам будет полезна:

Контрольная работа по статистике

Пример оформления заказа №1.

Сформировать 3 группы рабочих по средней зарплате. Известно, что самая высокая з/пл 9200 руб., самая низкая 5600 руб.

1) Определяем величину интервала по формуле:

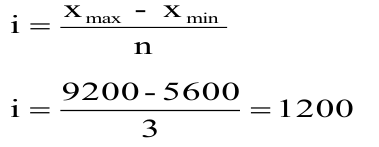
2) Сформируем группы рабочих по средней з/пл
1 гр. 5600 – 6800
2 гр. 6800 – 8000
3 гр. 8000 — 9200

4. Первым и наиболее простым способом обобщения статистических данных являются ряды распределения.

Статистическим рядом распределения называют численное распределение единиц совокупности по изучаемому признаку. В зависимости от признака ряды делятся на вариационные (количественные) и атрибутивные (качественные).

Вариационные ряды могут быть дискретными или интервальными.

Дискретный ряд распределения — это ряд, в котором численное распределение признака выражено одним конечным числом (например, распределение рабочих по разрядам).

Интервальный ряд распределения — это ряд, в котором значения признака заданы в виде интервала. Интервалы в рядах распределения могут быть неравными — прогрессивно возрастающими или прогрессивно убывающими. Это характерно для совокупностей с большой колеблемостью значений признака.

Элементы рядов распределения:

1. Варианта — это отдельное значение варьирующего признака, которое он принимает в ряду распределения.

2. Частота — это число, которое показывает, сколько раз встретилась варианта в данной совокупности.

При построении интервальных рядов распределения необходимо определить:
— какое число групп следует образовать;
— какие взять интервалы (равные, неравные, закрытые, открытые).

Эти вопросы решаются на основе экономического анализа сущности изучаемых явлений, поставленной цели и характера изменений признака.

Интервалы не должны быть:
— слишком широкими, так как в противном случае качественно различные объекты могут попасть в одну и ту же группу (нельзя, например, строить такие возрастные интервалы: 0—15 лет; 16—30 лет),
— не должны быть слишком узкими, поскольку и в этом случае число единиц в той или иной группе окажется незначительным и характеристики групп не будут типичными.

Интервальные ряды изображают — на графике с помощью гистограмм.

Дискретные ряды изображают — с помощью полигона распределения.

Обобщение данных и виде ряда распределения позволяет видеть вариацию и состав совокупности по изучаемому признаку, сравнивать между собой группы, изучать их в динамике.

Пример оформления заказа №2.

Сделать группировку рабочих по стажу и построить:

1) Вариационный дискретный ряд.
2) Вариационный интервальный ряд, образовав 2 группы с равными интервалами.
3) Указать варианту и частоту.
Данные о стаже рабочих:

1) Ряд распределения рабочих по стажу

Вид РР: вариационный дискретный ряд.
Варианта: стаж работы
Частота: число рабочих

2) Ряд распределения рабочих по стажу

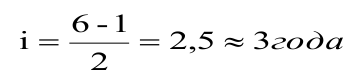
Вид РР: вариационный интервальный ряд.
Варианта: стаж работы
Частота: число рабочих

5. Результаты группировок находят свое выражение в виде сводных таблиц.

Таблица — это компактное изображение собранного материала в виде системы строк и столбцов, на пересечении которых приводятся данные, характеризующие изучаемое явление.

Статистическая таблица состоит из следующих элементов:

общий заголовок — отражает суть всей таблицы, содержит указание на характеризуемый признак объекта исследования, время, место наблюдения (иногда единицы измерения признака);
подлежащее — характеризуемый в таблице объект исследования (находится в левой части таблицы по строкам);
сказуемое — показатели, характеризующие подлежащее (располагается в верхней части по графам);
итоговая строка — может находиться в начале (тогда сопровождается нижеследующей строкой «в том числе») или в конце подлежащего. В тех графах итоговой строки, и которых по смыслу не могут быть подсчитаны результаты, ставится «X»;
цифровые данные — количественная характеристика исследуемого объекта (в случае отсутствия данных ставится «..» или пишется «нет сведений», а в случае отсутствия типа явления ставится «-»);
сетка — пересечение горизонтальных и вертикальных линий.

Все таблицы можно разделить на три группы:

1.Таблицы простые, или перечневые, в которых содержатся сводные показатели или перечень отдельных объектов без расчленения совокупности на группы.

2.Групповые таблицы, в которых статистическая совокупность расчленена на отдельные группы и каждая из этих групп охарактеризована рядом показателей.

3.Комбинационные таблицы, в которых статистическая совокупность разбита на группы по нескольким признакам (таким образом, в таблице получается комбинация групп).

По построению сказуемого различают:
— простые;
— комбинированные таблицы.

При простой разработке каждая графа сказуемого отдельно друг от друга характеризует подлежащее. При комбинированной таблице показатели сказуемого разрабатываются в сочетании друг с другом.

6. Графическое представление статистической информации применяется для более наглядного отображения исследуемых процессов.

Статистические графики — это условные изображения статистических данных в виде точек, линий или фигур,

Схематически все множество графических представлений статических данных разделяют на два класса:
— диаграммы;
— линейные изображения.

Выбор вида применяемого графика зависит от отображаемых данных. Например, для изображения структурного распределения совокупности, как правило, применяется круговая диаграмма.

Статистический график состоит из следующих элементов:
графический образ — геометрические значки, с помощью которых выражаются статистические показатели;
поле графика — ограниченная плоскость, на которой располагается график;
масштабные ориентиры — система мер и шкал, принятых для отображения данных.

К классу линейных графиков относятся:
— полигон,
— кумулятивная кривая,
— кривая концентрации,
— огива.

Полигоном частот называют ломаную, отрезки которой соединяют точки 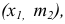… , 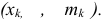Иногда крайние точки соединяют с точками, имеющими нулевую ординату.

Кумулятивная кривая (кривая сумм) — ломаная, составленная по последовательно суммированным, т.е. накопленным частотам или относительным частотам. При построении кумулятивной кривой дискретного признака на ось абсцисс наносятся значения признака, а ординатами служат нарастающие итоги частот. Соединением вершин ординат прямыми линиями получают кумуляту.

При построении кумуляты интервального признака на ось абсцисс откладываются границы интервалов и верхним значениям присваивают накопленные частоты. Кумулятивную кривую называют полигоном накопленных частот.

Если на ось ординат нанести значение признака, а накопленные частоты — на ось абсцисс, то получим кривую, называемую огивой.

Диаграмма — это графическое изображение, наглядно показывающее соотношение между сравниваемыми величинами. Диаграммы бывают различных видов:
— полосовые (ленточные),
— столбиковые,
— квадратные,
— круговые,
— секторные,
— фигурные,
— радиальные,
— знак Варвара.

Основным видом столбиковых диаграмм являются гистограммы.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основанием которых служат частотные интервалы длины, а высоты равны отношению Мi/h (плотность частоты). Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними на расстоянии Мi/h проводят отрезки, параллельные основанию.

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основанием которых случат частичные интервалы длиной h, а высоты раины Wi/h. Гистограмма относительных частот — аналог плотности распределения непрерывной случайной величины. Иногда высоты прямоугольников и гистограмме не делят на h, но указывают над столбиками значение высоты и над осью ординат пишут, что ее значение надо делить на h. Такую гистограмму называют масштабированной.

При построении квадратных и круговых диаграмм площади квадратов или кругов выражают изображаемые величины.

Круговые секторные диаграммы применяют для графического изображения составных частей целого. Чтобы легче различать сектора, используют различную раскраску или штриховку.

Радиальные диаграммы строятся в полярной системе координат и используются для изображения признаков, периодически изменяющихся во времени (в большинстве своем сезонных колебаний). Вычисляется среднее арифметическое, затем строится окружность радиуса, равного среднему арифметическому. Данная окружность делится на нужное число секторов (обычно 12) и на каждом радиальном направлении откладываются точки в соответствии со значениями Xi.

Фигурные диаграммы строятся двумя основными способами: данные изображаются либо фигурами различных размеров, либо разной численностью фигур одинакового размера.

Диаграмма «знак Варзара» названа в честь русского статистика. С помощью данной диаграммы можно изображать многомерные признаки на плоскости посредством прямоугольников с разным соотношением между основанием и высотой. Одна из компонент признака изображается основанием прямоугольника, вторая — его высотой, третья равна произведению двух других размером получившейся площади.

Возможно эта страница вам будет полезна:

Заказать работу по статистике

Средние величины

Понятие и расчет средних величин

Средняя величина — обобщающий показатель, который выражает типичные черты и дает обобщающую количественную характеристику какого-либо уровня какого-либо варьирующего признака по совокупности однородных явлений.

Введем следующие понятия и обозначения:
признак, по которому находится средняя, называется осредняемым признаком и обозначается x ;
величина осредняемого признака у каждой единицы совокупности называется индивидуальным его значением, или вариантами, и обозначается как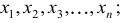
частота – это повторяемость индивидуальных значений признака, обозначается буквой f.

В статистике применяют различные виды средних величин:

1) простые (невзвешенные) – когда отдельные значения изучаемой совокупности не повторяются;

2) взвешенные – когда отдельные значения изучаемой совокупности повторяются.

Средняя арифметическая простая – наиболее распространенный вид средней. Она исчисляется в тех случаях, когда объем осредняемого признака образуется как сумма его значений у отдельных единиц изучаемой статистической совокупности.

В зависимости от характера исходных данных средняя арифметическая x определяется следующим образом.

Пример оформления заказа №3.

Предположим, что требуется вычислить средний стаж десяти работников торгового предприятия 6, 5, 4, 3, 3, 4, 5, 4, 5, 4, т.е. дан ряд одиночных значений признака, тогда х рассчитывается как

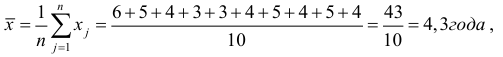
т.е. как средняя арифметическая невзвешенная делением количества свободного признака на число показаний:

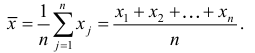
Часто приходится рассчитывать среднее значение признака по ряду распределения, когда одно и то же значение признака встречается несколько раз. Объединив данные по величине признака (т.е. сгруппировав) и подсчитав число случаев повторения каждого из них, мы получим следующую таблицу.

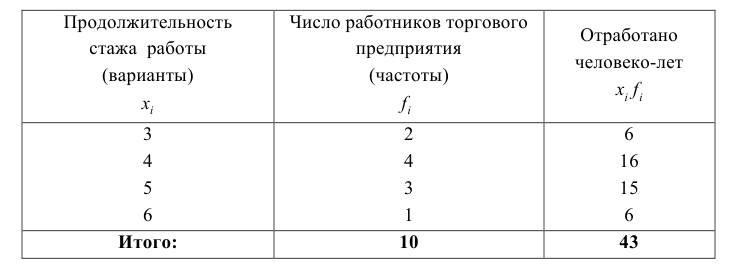
Тогда средняя вычисляется по формуле средней арифметической взвешенной:

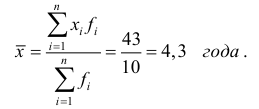
Часто вычисление средних величин приходится производить и по данным, сгруппированным в виде интервальных рядов распределения, когда варианты признака, из которых исчисляется средняя, представлены в виде интервалов (от – до).

Для вычисления средней величины надо в каждом интервале определить серединное значение x’ , после чего произвести взвешивание обычным порядком x’f. В закрытом интервале серединное значение определяется как полусумма значений нижней и верхней границ. Иногда задача исчисления средней по величинам интервального ряда осложняется тем, что неизвестны крайние границы начального и конечного интервалов. В этом случае предполагается, что расстояние между границами данного интервала такое же, как и в соседнем интервале.

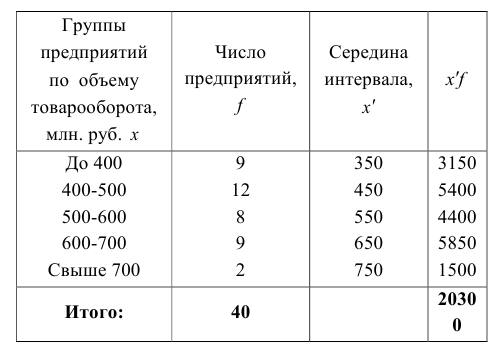
Пример оформления заказа №4.

Объем товарооборота в среднем на одно предприятие составит:

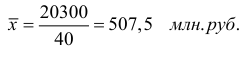
В данном случае для расчета применялась средняя арифметическая взвешенная из интервального ряда.

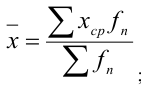
где X ср – серединное значение интервала.

Необходимо отметить, что изложенный прием исчисления средней является вынужденным в том случае, когда нет прямых данных о конкретной величине отдельных вариантов. Этот прием основан на предположении, что отдельные конкретные варианты равномерно распределены внутри интервала. Однако в действительности распределение отдельных вариантов в пределах интервала может оказаться неравномерным, и тогда середина интервала будет в той или иной степени отличаться от принятой средней. Это может повлиять на правильность общей средней, исчисленной по данным интервального ряда.

Необходимо отметить, что, хотя мы и используем для расчета средней из интервального ряда формулу средней арифметической взвешенной, исчисленная средняя не является точной величиной, так как в результате умножения средних значений групп на их численность мы не получим действительного значения. Сходство исчисленной средней со средней взвешенной лишь в методе вычисления. Здесь взяты не индивидуальные значения вариант, а условные средние каждой группы. Их взвешивание имеет чисто формальный характер.

Степень расхождения зависит от ряда причин:

1) число вариант: Чем больше число вариант, тем вероятнее, что середина интервала будет мало отличаться от групповой средней. Если же на каждую группу приходится малое число единиц, групповые средние могут находиться не только в середине, но и вблизи верхней либо нижней границы интервала. Если же наблюдений много и они более или менее равномерно распределяются в пределах интервала, то средняя величина в группе будет приближаться к середине интервала.

2) величина интервала: Если интервал невелик, то и ошибка будет незначительной, так как фактически групповая средняя будет мало отличаться от середины интервала.

3) характер распределения: Чем симметричнее распределение, тем ошибка меньше.

4) принцип построения интервального ряда: При равных интервалах середина построения его будет ближе примыкать к средней по данной группе. Кроме того, при наличии открытых интервалов к этому добавляются неточности, связанные с условным установлением неизвестных границ.

Средняя гармоническая – это величина, обратная средней арифметической. Когда статистическая информация не содержит частот по отдельным вариантам совокупности, а представлена как их произведение, применяется формула средней гармонической взвешенной

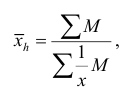
где M – величина общего объема, т.е. M = xf.

Так, например, расчет средней цены выражается отношением:

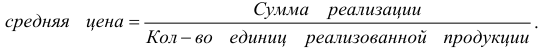
Пример оформления заказа №5.

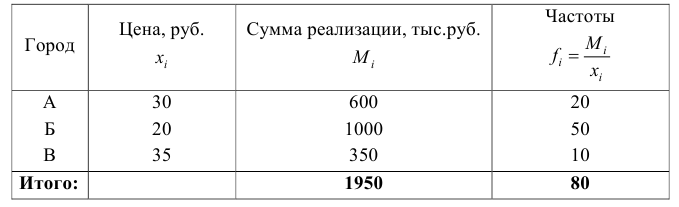
Величина суммы реализации, т. е. показателя, который находится в числителе исходного отношения, известна. Для определения неизвестной величины – количества реализованных единиц – нужно отдельно по каждому виду товара разделить сумму реализации на цену:

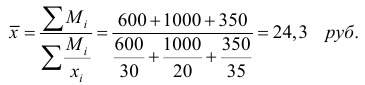
При определении средней цены, используя невзвешенную среднюю арифметическую, получим среднюю, которая не отражает объема реализации, т.е. нереальна:

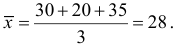
Как видно, средняя гармоническая является превращенной формой арифметической средней. Вместо гармонической всегда можно рассчитать среднюю арифметическую, но для этого сначала нужно определить веса отдельных значений признака.

В том случае, если объемы явлений, т. е. произведения, по каждому признаку равны, применяется средняя гармоническая (простая).

Пример оформления заказа №6.

Две автомашины прошли один и тот же путь: одна со скоростью 60 км/ч, а вторая – 80 км/ч, тогда средняя скорость составит:

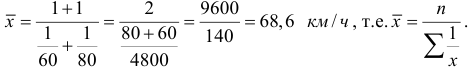
Средняя геометрическая – это величина, используемая как средняя из отношений или в рядах распределения, представленных в виде геометрической прогрессии. Этой средней удобно пользоваться, когда уделяется внимание не абсолютным разностям, а отношениям двух чисел. Поэтому средняя геометрическая используется в расчетах среднегодовых темпов роста.

Структурные средние величины

Для характеристики структуры вариационных рядов применяются показатели особого рода, которые можно назвать структурными средними.

Мода – значение признака, наиболее часто встречающееся в исследуемой совокупности.

Медиана – значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности.

Для дискретных вариационных рядов модой будет значение варианта с наибольшей частотой. Вычисление медианы в дискретных рядах распределения имеет специфику. Если такой ряд распределения имеет нечетное число членов, то медианой будет вариант, находящийся в середине ранжированного ряда. Если ранжированный ряд распределения состоит из четного числа членов, то медианой будет средняя арифметическая из двух значений признака, расположенных в середине ряда.

Рассмотрим определение моды и медианы по несгруппированным данным.

Пример оформления заказа №7.

Предположим, рабочие бригады, состоящей из 9 человек имеют следующие тарифные разряды: 4 3 4 5 3 3 6 2 6.

Так как в данной бригаде больше всего рабочих 3-го разряда этот тарифный разряд и будет модальным.

Для определения медианы необходимо провести ранжирование:
2 3 3 3 4 4 5 6 6.

Центральным в этом ряду является рабочий 4-го разряда, следовательно, данный разряд и будет медианным.

Если мода отражает типичный, наиболее распространенный вариант значения признака, то медиана практически выполняет функции средней для неоднородной, не подчиняющейся нормальному закону распределения совокупности. Проиллюстрируем ее познавательное значение следующим примером.

Пример оформления заказа №8.

Допустим, нам необходимо дать характеристику среднего дохода группы людей, насчитывающей 100 человек, из которых 99 имеют доходы в интервале от 100 до 200 долл. в месяц, а месячные доходы последнего составляют 50 000 долл.

Если мы воспользуемся средней арифметической, то получим средний доход, равный примерно 600 — 700 долл., который не только в несколько раз меньше дохода 100-го человека, но и имеет мало общего с доходами остальной части группы.

Медиана же, равная в данном случае 163 долл., позволит дать объективную характеристику уровня доходов 99% данной группы людей.

Пример оформления заказа №9.

Рассмотрим определение моды и медианы по сгруппированным данным (рядам распределения).

Предположим, распределение рабочих уже не отдельной бригады, а всего предприятия в целом по тарифному разряду имеет следующий вид:

Определение моды по дискретному вариационному ряду не составляет большого труда — наибольшую частоту (60 человек) имеет 5-й тарифный разряд, следовательно, он и является модальным.

Для определения медианного значения признака по следующей формуле находят номер медианной единицы ряда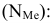

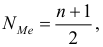где n – объем совокупности.

В нашем случае: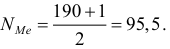

Полученное дробное значение, всегда имеющее место при четном числе единиц в совокупности, указывает, что точная середина находится между 95-м и 96-м рабочими. Необходимо определить, к какой группе относятся рабочие с этими порядковыми номерами. Это можно сделать, рассчитав накопленные частоты. Медианным является 4-й тарифный разряд.

В отличие от дискретных вариационных рядов определение моды и медианы по интервальным рядам требует проведения определенных расчетов на основе следующих формул:

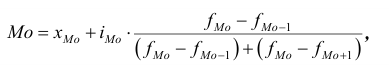
где 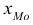– нижняя граница значения интервала, содержащего моду; 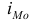– величина модального интервала; 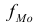— частота модального интервала; 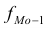– частота интервала, предшествующего модальному; 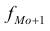– частота интервала, следующего за модальным.

Медиана интервального ряда распределения определяется по формуле:

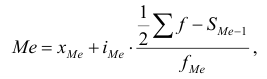
где 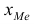– нижняя граница значения интервала, содержащего медиану;
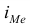– величина медианного интервала;
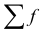– сумма частот;
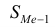– сумма накопленных частот, предшествующих медианному интервалу;
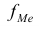– частота медианного интервала.

Пример оформления заказа №10.

Рассчитаем моду и медиану по данным таблицы: Распределение семей города по размеру среднедушевого дохода в январе 1998г.

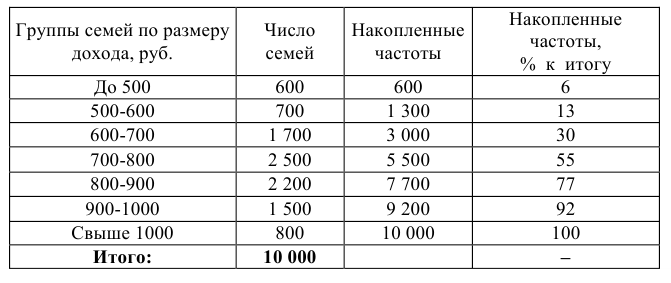
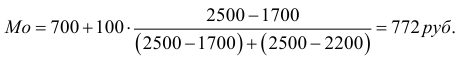
Следовательно, наибольшее число семей имеют среднедушевой доход 772 руб.

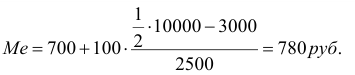
Таким образом, половина семей города имеет среднедушевой доход менее 780 руб., остальные семьи – более 780 руб.

Показатели вариации

Понятие вариации

Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака. Она возникает в результате того, что его индивидуальные значения складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае.

Средняя величина, как уже отмечалось, – это абстрактная, обобщающая характеристика признака изучаемой совокупности, но она не показывает строения совокупности, которое весьма существенно для ее познания. Средняя величина не дает представления о том, как отдельные значения изучаемого признака группируются вокруг средней, сосредоточены ли они вблизи или значительно отклоняются от нее. В некоторых случаях отдельные значения признака близко примыкают к средней арифметической и мало от нее отличаются. В таких случаях средняя хорошо представляет всю совокупность. В других, наоборот, отдельные значения совокупности далеко отстают от средней, и средняя плохо представляет всю совокупность.

Колеблемость отдельных значений характеризуют показатели вариации.

Термин «вариация» произошел от латинского variatio – изменение, колеблемость, различие. Однако не всякие различия принято называть вариацией. Под вариацией в статистике понимают такие количественные изменения величины исследуемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов. Различают вариацию признака: случайную и систематическую.

Анализ систематической вариации позволяет оценить степень зависимости изменений в изучаемом признаке от определяющих ее факторов. Например, изучая силу и характер вариации в выделенной совокупности, можно оценить, насколько однородной является данная совокупность в количественном, а иногда и качественном отношении, а, следовательно, насколько характерной является исчисленная средняя величина. Степень близости данных отдельных единиц 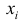к средней измеряется рядом абсолютных, средних и относительных показателей.

Абсолютные и средние показатели вариации и способы их расчета

Для характеристики колеблемости признака используется ряд показателей. Наиболее простой из них – размах вариации, определяемый как разность между наибольшим (max) и наименьшим (min) значениями вариант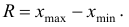

Размах вариации улавливает только крайние отклонения и не отражает отклонений всех вариант в ряду. Однако легкость вычислений и простота истолкования обусловили широкое применение этого показателя.

Чтобы дать обобщающую характеристику распределению отклонений, исчисляют среднее линейное отклонение d, которое учитывает различия всех единиц изучаемой совокупности. Среднее линейное отклонение определяется как средняя арифметическая из отклонений индивидуальных значений от средней, без учета знака этих отклонений:

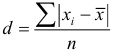– простое среднее линейное отклонение,

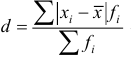– взвешенное среднее линейное отклонение.

Среднее линейное отклонение как меру вариации признака применяют в статистической практике редко. Во многих случаях этот показатель не устанавливает степень рассеивания.

На практике меру вариации более объективно отражает показатель дисперсии ( 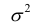– средний квадрат отклонений), определяемый как средняя из отклонений, возведенных в квадрат:

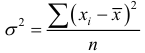– простая дисперсия,
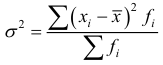– взвешенная дисперсия.

Корень квадратный из дисперсии 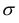среднего квадрата отклонений представляет собой среднее квадратическое отклонение:

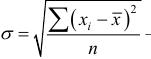– простое среднее квадратическое отклонение,
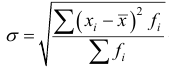– взвешенное среднее квадратическое отклонение.

Среднее квадратическое отклонение является мерилом надежности средней. Чем меньше среднее квадратическое отклонение, тем лучше средняя арифметическая отражает собой всю представляемую совокупность.

Показатели относительного рассеивания

Для характеристики меры колеблемости изучаемого признака исчисляются показатели колеблемости в относительных величинах. Они позволяют сравнивать характер рассеивания в различных распределениях (различные единицы наблюдения одного и того же признака в двух совокупностях, при различных значениях средних, при сравнении разноименных совокупностей). Расчет показателей меры относительного рассеивания осуществляют как отношение абсолютного показателя рассеивания к средней арифметической, умножаемое на 100%.

1. Коэффициент осцилляции отражает относительную колеблемость крайних значений признака вокруг средней:

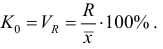
2. Относительное линейное отклонение (Линейный коэффициент вариации) характеризует долю усредненного значения абсолютных отклонений от средней величины:

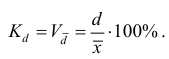
3. Коэффициент вариации:

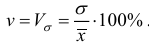
Этот коэффициент является критерием надежности средней величины. Если он < 33%, можно говорить об однородности совокупности и надежности средней для этой совокупности.

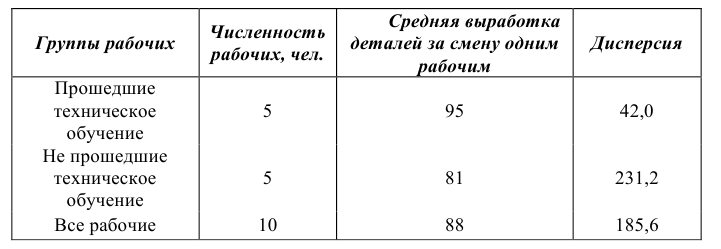
Пример оформления заказа №11.

Производительность труда двух групп рабочих одного из цехов НПО «Циклон»:

Рассчитаем общую и групповые средние и дисперсии:

Итоги вычисления представлены в таблице:

Абсолютные и относительные величины

Понятие об абсолютных величинах, их значение и виды.

1. АБСОЛЮТНЫЕ ВЕЛИЧИНЫ (АВ) – это обобщающие показатели, которые получены в результате сводки путем суммирования статистических данных.

Абсолютные величины выражают объемы, уровни и размеры общественных явлений в конкретных условиях места и времени.

ЗНАЧЕНИЕ: Их широко используют в практике торговли, применяют в анализе и прогнозировании коммерческой деятельности. На их основе составляют хозяйственные договоры, оценивают объем спроса на конкретные товары, изделия.

По способу выражения размеров изучаемых явлений АВ подразделяются на индивидуальные и суммарные.

Индивидуальные характеризуют размеры количественных признаков у отдельных единиц.

Например, выработку одного продавца за конкретный период и т.д. Этот вид показателей служит основанием при статистической сводке для включения, единиц объекта в группы, из которых, в свою очередь, можно выделить показатели численности совокупности и показатели объема признаков совокупности.

АВ характеризуют совокупности экономически сравнительно простые (численность магазинов, работников) и сложные (объем товарооборота, размер основных фондов).

АВ всегда числа именованные, имеющие определенную размерность, единицы измерения.

Натуральные единицы измерения в большинстве своем соответствуют природным или потребительским свойствам предмета, товара и выражается в физических мерах веса, длины и т.д.

Абсолютные величины измеряются и в стоимостных единицах – ценах. Это особенно важно в условиях рыночной экономики, которая не исключает и товарообмен (бартерные сделки) с другими регионами.

Значительно реже АВ выражается в трудовых единицах измерения – человеко-часах, человеко-днях.

Условно — натуральные единицы измерения используются тогда, когда необходимо суммировать величины, непосредственно непподдающиеся суммированию. Необходимо сделать пересчет натуральных единиц измерения по специальному коэффициенту:

К = Vизуч. явл. : Vявл., принятого за эталон.

Пример оформления заказа №12.

За отчетный период предприятие произвело следующие виды мыла и моющих средств:

Требуется определить общее количество выработанной предприятием продукции в условно-натуральных единицах измерения.

За условную единицу измерения принимается мыло 40% жирности.

Коэффициент перевода

Общий объем производства мыла и моющих средств по видам

Таблица 5.2

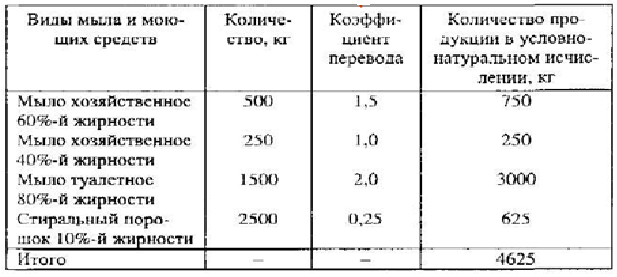
2. ОТНОСИТЕЛЬНЫЕ ВЕЛИЧИНЫ (ОВ) – это обобщенные показатели, которые характеризуют числовую меру соотношения сопоставляемых абсолютных величин (АВ).

ЗНАЧЕНИЕ: заключается в том, что с их помощью дается оценка выполнения плана или договора, составляется прогноз на будущее, изучается динамика и структура явления. Эти величины используются при анализе.

Получаются ОВ путем деления АВ на другую АВ. Величина, которая находится в числителе называется текущей (отчетной).

А величина в знаменателе – базисной (базой сравнения, основанием).

ОВ как правило, не имеют единиц измерения, но имеют форму выражения. Она зависит от того, какое числовое значение имеет база сравнения:

1. Если она принимается за 1 (единицу), то ОВ выражается в коэффициентах (К) и показывает во сколько раз отчетная величина больше или меньше базистой. Как правило, степень точности

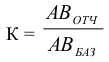
2. Если база сравнения принята за 100 единиц, то ОВ выражается в процентах. Процент должен быть рассчитан со степенью точности 0,1.

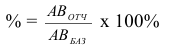
3. Если база сравнения принята за 100 единиц, то в промилле

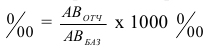
4. Если за 10000, то в децимилле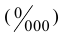

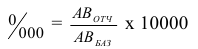
Последние две формы выражения обычно применяются в том случае, если отчетная величина значительно меньше базисной (например, при расчете демографических коэффициентов).

Возможно эта страница вам будет полезна:

Задачи статистики: предмет, метод, теория

Виды относительных величин

При анализе статистической информации может быть использованы следующие виды относительных величин (ОВ).

1) ОВ ВЫПОЛНЕНИЯ ДОГОВОРНЫХ ОБЯЗАТЕЛЬСТВ.

Применятся, если нужно дать оценку выполнения обязательств, предусмотренным договором. При расчете фактический уровень выполнения договорных обязательств разделить на уровень предусмотренный договором. Выражается в %.

2) ОВ ВЫПОЛНЕНИЯ ПЛАНА (процент выполнения плана)

Применяется, если нужно дать оценку выполнения плана по каким-либо показателям. При расчете фактические данные отчетного периода делятся на плановые данные этого же периода. Выражается в %. 38

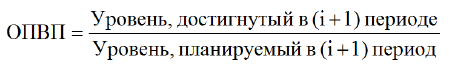
Валовой доход фирмы, занимающейся производством и продажей сложной бытовой техники, в феврале отчетного года составил 2055,5 тыс. руб. при плане 1800 тыс. руб.

Определить степень выполнения плана по валовому доходу фирмы в феврале текущего года.

Решение. 2055,5/1800*100% = 114,2%

План по валовому доходу в феврале текущего года фирмой выполнен на 114,2 %, то есть перевыполнение плана составило 14,2%.

3) ОВ ПЛАНОВОГО ЗАДАНИЯ (плановый темп роста)

Применяется, если нужно составить прогноз на будущий период. При расчете плановые данные текущего периода нужно разделить на фактические данные предыдущего (базисного) периода. Выражается обычно в %, можно в коэффициентах.

В январе отчетного года валовой доход фирмы, занимающейся производством и продажей сложной бытовой техники, составил 1500 тыс. руб., в феврале планируется товарооборот в 1800 тыс. руб.

Определить относительную величину планового задания.

Решение. 1800/1500*100% = 120 %

Таким образом, в феврале планируется увеличение валового дохода фирмы на 20 %.

4) ОВ ДИНАМИКИ (фактический темп роста)

Применяется, если нужно изучить изменение явления во времени. При расчете фактические данные отчетного периода нужно разделить на фактические данные предыдущего (базисного) периода. Выражается как в коэффициентах, так и в процентах.

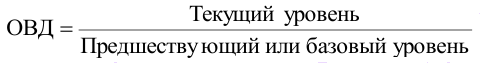
5) ОВ СТРУКТУРЫ (удельный вес)

Применяется в том случае, если нужно определить удельный вес каждой части явления. При расчете нужно каждую часть разделить на явление в целом. Сумма удельных весов должна быть равна 100%, т.е. выражается в процентах.

6) ОВ СРАВНЕНИЯ

Применяется в том случае, если нужно сравнить одноименные величины на разных объектах прибыли (например: прибыль на разных предприятиях). Рассчитывается путем деления величины на одном объекте на такую же величину на другом объекте. Выражается как в процентах, так и в коэффициентах.

7) ОВ КООРДИНАЦИИ

Применяется, если нужно сопоставить разные части одного и того же явления. При расчете одна часть делится на другую. Имеет все формы выражения.
ОВК = Пn/ Пб,
где Пn — показатель, характеризующий n-ю часть совокупности; Пб — показатель, характеризующий часть совокупности, выбранную в качестве базы сравнения.

Имеются следующие данные о численности экономически активного населения одного из городов области по состоянию на начало 2003 г., тыс. чел.:
Численность экономически активного населения 125,1 в том числе:
занятых в экономике 96,4
безработных 28,7

Исчислить, сколько безработных приходится на 1000 чел. занятого населения.

Решение. 28,7/96,4*1000 = 297,7 чел.

Следовательно, на каждую 1000 чел. населения, занятого в экономике города, приходится примерно 298 безработных.

8) ОВ ИНТЕНСИВНОСТИ

Применяется для того, чтобы изучить степень распространения одних явлений среди других. При расчете нужно одно явление разделить на другое. В отличие от других ОВ может иметь единицы измерения (натуральные, трудовые, стоимостные). Например: фондоотдача.

Задача

По данным об объеме производства продукции ООО «Статус» в 2013, 2014 гг. рассчитать относительные величины выполнения плана, планового задания, динамики структуры. По результатам расчетов сделать вывод.

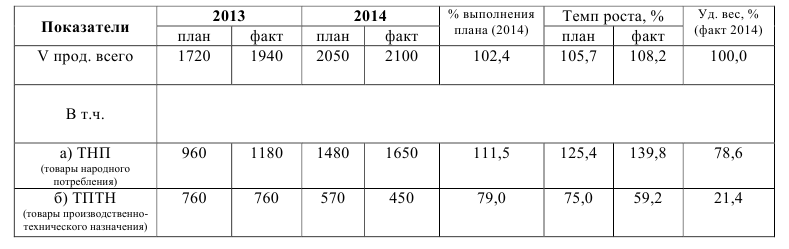
1) ОВ выполнения плана (2014г.)

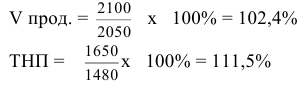
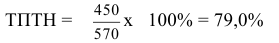
2) ОВ планового задания – плановый темп роста

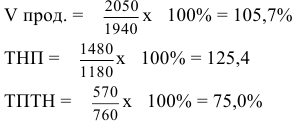
3) ОВ динамики – фактический темп роста

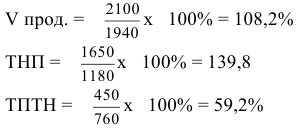
4) ОВ структуры – удельный вес (2014г. факт)

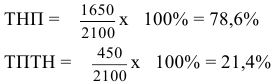
Выводы: План по объему продукции в 2014г. перевыполнен на 2,4%, в т.ч. по ТНП на 11,5%, а план по производству ТПТН не выполнен на 21,0%.
Было запланировано на 2014г. увеличение объема продукции на 5,7%, в т.ч. ТНП на 25,4%, а выпуск ТПТН должен был снизиться на 25,0%.
Фактически выпуск продукции увеличился на 8,2%, в т.ч. ТНП на 39,8%, а выпуск ТПТН снизился на 40,8 %. Удельный вес ТНП в 2014г. в общем объеме продукции составил 78,6%, а ТПТН – 21,4 %.

Ряды динамики

Понятие рядов динамика, их виды

Основная цель статистического изучения динамики развития социальноэкономических явлений состоит в выявлении и измерении закономерностей их развития во времени. Это достигается посредством, построения и анализа статистических рядов динамики.

Ряды динамики – числовые значения определенного стат. показателя в последовательные моменты или периоды времени.

В каждом ряду динамики имеются два основных элемента:

1) показатель времени t;

2) соответствующие им уровни развития изучаемого явления у.

Уровни рядов динамики отображают количественную оценку (меру) развития во времени изучаемого явления. Они могут выражаться абсолютными, относительными или средними величинами.

В качестве показаний времени в рядах динамики выступают либо определенные даты (моменты) времени, либо отдельные периоды (годы, кварталы, месяцы, сутки).

В зависимости от характера изучаемого явления уровни рядов динамики могут относиться или к определенным датам (моментам) времени, или к отдельным периодам. В соответствии с этим ряды динамики подразделяются на моментные и интервальные.

Моментные ряды динамики отображают состояние изучаемых явлений на определенные даты (моменты) времени.

Примером моментного ряда динамики является следующая информация о списочной численности работников магазина в 2013 г.:

Особенностью моментного ряда динамики является то, что в его уровни могут входить одни и те же единицы изучаемой совокупности. Так, основная часть персонала магазина, составляющая списочную численность на 01.01.2013 г., продолжающая работать в течение данного года, отображена в уровнях последующих периодов. Поэтому при суммировании уровней моментного ряда динамики может возникнуть повторный счет.

Посредством моментных рядов динамики в торговле изучают товарные запасы, состояние кадров, количество оборудования и других показателей, отображающих состояние изучаемых явлений на отдельные даты (моменты) времени.

Интервальные ряды динамики отображают итоги развития изучаемых явлений за отдельные периоды (интервалы) времени.

Примером интервального ряда динамики могут служить данные о розничном товарообороте магазина в 2010-2014 гг.:

Особенностью интервального ряда динамики является то, что каждый его уровень складывается из данных за более короткие интервалы (субпериоды) времени. Например, суммируя товарооборот за первые три месяца года, получают его объем за I квартал, а сумма товарооборота четырех кварталов дает объем товарооборота за год и т. д.

Свойство суммирования уровней за последовательные интервалы времени позволяет получать ряды динамики более укрупненных периодов.

Посредством интервальных рядов динамики в торговле изучается изменение во времени поступления и реализации товаров, суммы издержек обращения и других показателей, отображающих итоги функционирования (развития) изучаемых явлений за отдельные периоды.

Основным условием для получения правильных выводов при анализе рядов динамики является сопоставимость его элементов.

Ряды динамики формируются в результате сводки и обработки материалов периодического наблюдения. Повторяющиеся во времени (по отчетным периодам) значения одноименных показателей в ходе статистической сводки систематизируются в хронологической последовательности.

При этом каждый ряд динамики охватывает отдельные обособленные периоды, в которых могут происходить изменения, приводящие к несопоставимости отчетных данных с данными других периодов. Поэтому для анализа ряда динамики необходимо приведение всех составляющих его элементов к сопоставимому виду. Для этого в соответствии с задачами исследования устанавливаются причины, обусловившие несопоставимость анализируемой информации, и применяется соответствующая обработка, позволяющая производить сравнение уровней ряда динамики.

Для количественной оценки динамики социально-экономических явлений применяются следующие показатели:

— абсолютные приросты,
— темпы роста и прироста,
— темпы наращивания и др.

В основе расчета показателей рядов динамики лежит сравнение его уровней. В зависимости от применяемого способа сопоставления показатели динамики могут вычисляться на постоянной и переменной базах сравнения.

Для расчета показателей динамики на постоянной базе каждый уровень ряда сравнивается с одним и тем же базисным уровнем. Исчисляемые при этом показатели называются базисными. Для расчета показателей динамики на переменной базе каждый последующий уровень ряда сравнивается с предыдущим. Вычисленные таким образом показатели динамики называются цепными.

Важнейшим статистическим показателем динамики является абсолютный прирост, который определяется в разностном сопоставлении двух уровней ряда динамики в единицах измерения исходной информации.

Базисный абсолютный прирост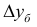 исчисляется как разность между сравниваемым уровнем 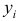; и уровнем, принятым за постоянную базу сравнения :

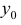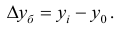
Цепной абсолютный прирост 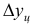– разность между сравниваемым уровнем 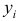и уровнем, который ему предшествует,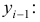

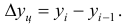
Абсолютный прирост может иметь и отрицательный знак, показывающий, насколько уровень изучаемого периода ниже базисного.

Между базисными и цепными абсолютными приростами имеется связь: сумма цепных абсолютных приростов 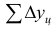равна базисному абсолютному приросту последнего периода ряда динамики :

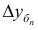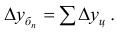
Распространенным статистическим показателем динамики является темп роста. Он характеризует отношение двух уровней ряда и может выражаться в виде коэффициента или в процентах. Базисные темпы роста 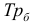исчисляются делением сравниваемого уровня на уровень, принятый за постоянную базу сравнения, :

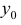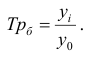
Цепные темпы роста 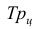исчисляются делением сравниваемого уровня i y на предыдущий уровень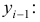

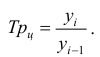
Если темп роста больше единицы (или 100%), то это показывает на увеличение изучаемого уровня по сравнению с базисным. Темп роста, равный единице (или 100%), показывает, что уровень изучаемого периода по сравнению с базисным не изменился. Темп роста меньше единицы (или 100%) показывает на уменьшение уровня изучаемого периода по сравнению с базисным. Темп роста всегда имеет положительный знак.

Между базисными и цепными темпами роста имеется взаимосвязь: произведение последовательных цепных темпов роста равно базисному темпу роста, а частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста.

Темпы прироста характеризуют абсолютный прирост в относительных величинах. Исчисленный в процентах темп прироста показывает, на сколько процентов изменился сравниваемый уровень с уровнем, принятым за базу сравнения.

Базисный темп прироста 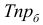вычисляется делением сравниваемого базисного абсолютного прироста, на уровень, принятый за постоянную базу сравнения.

Цепной темп прироста 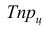– это отношение сравниваемого цепного абсолютного прироста к предыдущему уровню:

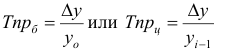
Между показателями темпа прироста и темпа роста имеется взаимосвязь: Тпр = Тр(%) — 100% (при выражении темпа роста в процентах) или Тпр = Тр — 1 (при выражении темпа роста в коэффициентах). Последние две формулы дают 2-й способ вычисления темпа прироста.

Абсолютное значение 1% прироста – это отношение абсолютного прироста к темпу прироста:

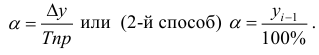
Средние показатели ряда

Средний уровень ряда динамики характеризует типическую величину абсолютных уровней.

В интервальных рядах динамики средний уровень определяется делением суммы уровней на их число:

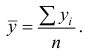
В моментном ряду динамики с равностоящими датами времени средний уровень определяется по формуле средней хронологической:

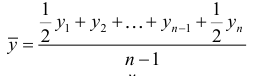
У нас в примере ряд интервальный, следовательно:

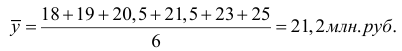
Средний абсолютный прирост представляет собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики. Для определения среднего абсолютного прироста сумма цепных абсолютных приростов делится на их число:

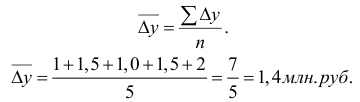
Средний темп роста – обобщающая характеристика индивидуальных темпов роста ряда динамики. Для определения среднего темпа роста применяется формула средней геометрической из показателей коэффициентов роста:

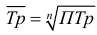, где n – число темпов роста, или
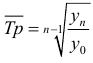, где n — 1 – число уровней ряда, уменьшенное на 1.

Средний темп прироста можно определить на основе взаимосвязи между темпами роста и прироста. При наличии данных о средних темпах роста для получения средних темпов прироста используется зависимость:

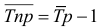(при выражении среднего темпа роста в коэффициентах),
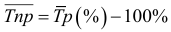(при выражении среднего темпа роста в процентах).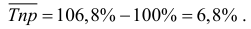

Среднее абсолютное содержание 1% прироста вычисляется делением суммы значений абсолютного содержания 1% прироста на их число:

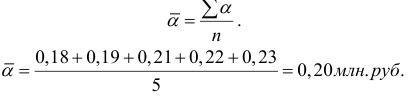
Графически ряды динамики могут быть представлены в виде линейного графика, диаграммы, структурной диаграммы, картограммы, картосхемы.

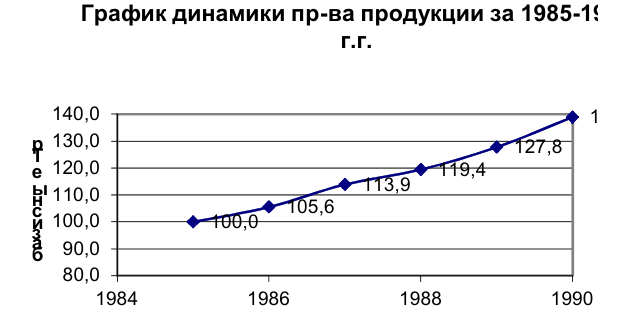
Задача

Численность рабочих предприятия по месяцам года характеризуются следующими данными (чел.):

Известно, что среднесписочная численность рабочих за III квартал составила 2172 чел., за IV квартал – 2181 чел.

Определите среднесписочную численность рабочих за I-е полугодие, за II-е полугодие и за год в целом.

Решение: Т.к. приведен моментный ряд, расчет производится по средней хронологической:
За I-е полугодие:

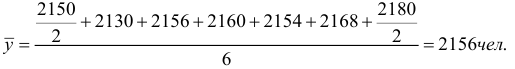
По кварталам:

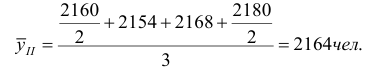
За II-е полугодие: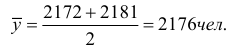
За год: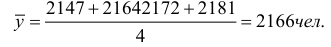

Задача

Ежегодный прирост продукции промышленного предприятия за 2010-2014 г.г. характеризуется следующими данными (в % к предыдущему году):

Исчислите базисные темпы роста (2010 = 100) пр-ва продукции за эти годы и среднегодовой темп роста.

Решение:
Т.к. Тпр = Тр(%)- 100% , то темпы прироста составят соответственно: (см. таблицу). Затем воспользуемся формулой, что произведение цепных темпов равно базисную, предварительно сделав базисным 2010 год.

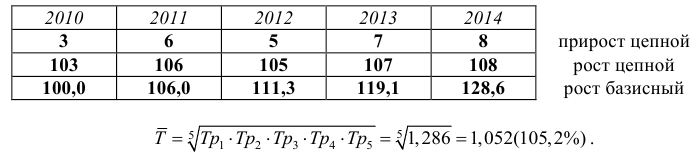
Индексный метод в статистике

Статистический индекс

Важное значение в статистических исследованиях коммерческой деятельности имеет индексный метод. Полученные на основе этого метода показатели используются для характеристики развития анализируемых показателей во времени, по территории, изучения структуры и взаимосвязей, выявления роли факторов в изменении сложных явлений.

Статистический индекс – это относительная величина сравнения сложных совокупностей и отдельных их единиц. При этом под сложной понимается такая статистическая совокупность, отдельные элементы которой непосредственно не подлежат суммированию.

Например, ассортимент продовольственных товаров состоит из ударных разновидностей, первичный учет которых на производстве и в оптовой торговле ведется в натуральных единицах измерения: молоко – в литрах, мясо – в центнерах, яйцо – в штуках, консервы – в условных банках и т.д.. Для определения общего объема производства и реализации продовольственных товаров суммировать данные учета разнородных товарных масс в натуральных измерителях нельзя. Не подлежат непосредственному суммированию и данные о количестве произведенных и реализованных различных видов непродовольственных товаров. Было бы, например, бессмысленно для получения общего объема реализации суммировать данные о продаже тканей (в метрах), костюмов (в штуках), обуви (в парах) и т. д.

В этих сложных статистических совокупностях единицами наблюдения являются товары с различными потребительскими свойствами. Данные о натуральновещественной форме реализации отдельных товарных разновидностей непосредственному суммированию не подлежат. Для получения в сложных статистических совокупностях обобщающих (суммарных) величин прибегают к индексному методу.

Основой индексного метода при определении изменений в производстве и обращении товаров является переход от натурально-вещественной формы выражения товарных масс к стоимостным (денежным) измерителям. Именно посредством денежного выражения стоимости отдельных товаров устраняется их несравнимость как потребительных стоимостей и достигается единство.

Экономическое содержание индексов заключается в том, что они характеризуют изменение индексируемого показателя в отчетном периоде по сравнению с базисным, изменение явления в пространстве или в динамике, т.е. за целый ряд лет.

Индексный метод решает следующие задачи:

1) характеристика общего изменения сложного экономического явления (пр. выявление характера взаимосвязи изменения товарооборота с изменением цен).

2) выделение в показателе изменения сложного явления влияния одного из факторов путем абстрагирования от влияния др. факторов. Для удобства в теории статистики разработана определенная символика. Каждая величина, изменение которой интересует (индексируемая величина) имеет свое символическое обозначение:

p – цена единицы изделия или товара,
z – себестоимость единицы продукции,
t – трудоемкость единицы продукции (затраты времени на пр-во 1 шт. продукции),
w– производительность труда (величина, обратная трудоемкости).

Перечисленные выше показатели являются качественными.

q – объем произведенной или реализованной продукции в натуральном измерении – это количественный показатель.

Тогда можно выразить еще некоторые величины:

pq– стоимость реализованной продукции (товарооборот, кассовая выручка),
zq – денежные затраты на выпуск продукции,
tq – трудовые затраты на производство продукции,
wq– временные затраты на производство.

Общие и индивидуальные индексы

В зависимости от степени охвата подвергнутых обобщению единиц изучаемой совокупности индексы подразделяются на индивидуальные, общие и групповые.

Индивидуальные индексы, характеризуют изменения отдельных единиц статистической совокупности. Так, например, если при изучении оптовой реализации продовольственных товаров определяются изменения в продаже отдельных товарных разновидностей, то получают индивидуальные (однотоварные) индексы.

Общие индексы выражают сводные (обобщающие) результаты совместного изменения всех единиц, образующих статистическую совокупность. Например, показатель изменения объема реализации товарной массы продуктов питания по отдельным периодам будет общим индексом физического объема товарооборота Из общих индексов выделяют иногда групповые индексы (субиндексы), охватывающие только часть (группу) единиц в изучаемой статистической совокупности.

Важной особенностью общих индексов является то, что они обладают синтетическими и аналитическими свойствами.

Синтетические свойства индексов состоят в том, что посредством индексного метода производится соединение (агрегирование) в целое разнородных единиц статистической совокупности.

Аналитические свойства индексов состоят в том, что посредством индексного метода определяется влияние факторов на изменение изучаемого показателя. Использование индексов в аналитических целях – один из важных аспектов экономических разработок. На основе изучения состава и роли факторов, выявления силы их действия осуществляются возможности квалифицированного управления развитием экономических процессов не только в нужном направлении, но и с заранее заданными параметрами.

Основным элементом индексного отношения является индексируемая величина. Под индексируемой величиной понимается значение признака статистической совокупности, изменение которой является объектом изучения. Так, при изучении изменения цен индексируемой величиной является цена единицы товара р. При изучении изменения физического объема товарной массы в качестве индексируемой величины выступают данные о количестве товаров в натуральных измерителях q.

Индивидуальные индексы принято обозначать i и снабжать подстрочным значком индексируемого показателя.

Индивидуальные индексы качественных показателей:

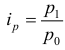– индекс цен,
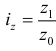– индекс себестоимости,
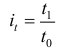– индекс трудоемкости,
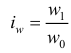– индекс производительности труда (прямой показатель),
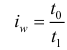– индекс производительности труда (обратный показатель).

Индивидуальный индекс количественного показателя: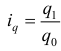
– индекс физического объема продукции или товарооборота.

Агрегатные (общие) индексы принято обозначать I .

Основной формой общих индексов являются агрегатные индексы. Свое название они получили от латинского слова «aggrega», что означает «присоединяю». В числителе и знаменателе общих индексов в агрегатной форме содержатся соединенные наборы (агрегаты) элементов изучаемых статистических совокупностей.

Достижение в сложных статистических совокупностях сопоставимости разнородных единиц осуществляется введением в индексные отношения специальных сомножителей индексируемых величин. В литературе такие сомножители называются соизмерителями. Они необходимы для перехода от натуральных измерителей разнородных единиц статистической совокупности к однородным показателям. При этом в числителе и знаменателе общего индекса изменяется лишь значение индексируемой величины, а их соизмерители являются постоянными величинами и фиксируются на одном уровне (текущего или базисного периода).

Это необходимо для того, чтобы на величине индекса сказывалось лишь влияние фактора, который определяет изменение индексируемой величины.

Учитывая требования увязки индексов в систему можно сформулировать следующие правила в отношении выбора периода, к которому относится вес (второй элемент индекса или соизмеритель):

1. При построении агрегатных индексов качественных показателей веса (количественные показатели) принимаются на уровне отчетного периода.

2. При построении агрегатных индексов количественных показателей соизмерители (кач. показатели) берутся на уровне базисного периода.

Агрегатные индексы качественных показателей:

1. 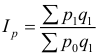– индекс цен (общее изменение цен по всем товарным группам).

Предложен немецким экономистом Г. Пааше. Поэтому индекс (1) принято называть индексом Пааше.

2. 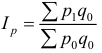– индекс цен Ласпейроса.

Индекс Пааше характеризует влияние изменения цен на стоимость товаров, реализованных в отчетном периоде.

Индекс Ласпейроса показывает влияние изменения цен на стоимость количества товаров, реализованных в базисном периоде.

Применение индексов Пааше и Ласпейроса зависит от цели исследования.

Если анализ проводится для определения экономического эффекта от изменения цен в отчетном периоде по сравнению с базисным, то применяется индекс Пааше, который отображает разницу между фактической стоимостью продажи товаров в отчетном периоде и расчетной стоимостью продажи этих же товаров по базисным ценам.

Если целью анализа является определение объема товарооборота при продаже в предстоящем периоде такого же количества товаров, что и в базисном периоде, но по новым ценам, то применяется индекс Ласпейроса. Этот индекс позволяет вычислять разность между суммой фактического товарооборота базисного периода и возможного объема товарооборота при продаже тех же товаров по новым ценам.

Эти особенности индекса Ласпейроса обусловливают его применение при прогнозировании объема товарооборота в связи с намечаемыми изменениями цен на товары в предстоящем периоде. Вместе с тем при изучении отчетных данных, когда целью анализа является количественная оценка изменения объема товарооборота в результате имевшегося изменения цен в отчетном периоде, для определения общего индекса цен и получаемого при этом экономического эффекта применяется формула Пааше

2. 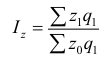– индекс себестоимости.

3. 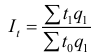– индекс трудоемкости.

4. 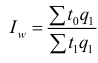– индекс производительности труда (обратный показатель).

Агрегатные индексы количественных показателей:

5. 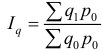– индекс физического объема товарооборота в сопоставимых (базисных) ценах,

6. 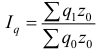– индекс физического объема продукции в ценах текущего периода.

Взаимосвязь индексов

Система взаимосвязанных индексов позволяет выявить и оценить роль отдельных факторов в изменении данного явления, т.е. показать, как изменился результативный показатель под влиянием каждого отдельного фактора.

1. 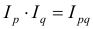индекс товарооборота в фактических ценах,

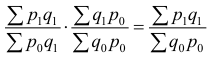
2. 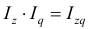– индекс затрат на продукцию,

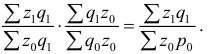
Система взаимосвязанных индексов используется на практике для определения роли отдельных факторов в общей динамике сложного явления и для определения по двум известным показателям третьего неизвестного.

Средневзвешенные индексы

Преобразование агрегатного индекса в средневзвешенный производится путем подстановки либо в числитель либо в знаменатель агрегатного индекса его значения через соответствующий индивидуальный индекс. Если такая замена сделана в числителе соотношения, индекс окажется преобразованным в средний арифметический, если в знаменателе, то в средний гармонический.

Практически замена делается обычно там, где в агрегатном индексе отсутствует условная экономическая величина.

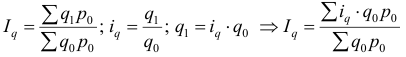– индекс физического объема средний арифметический, 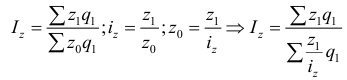– индекс себестоимости средний гармонический.

Индексный метод анализа динамики среднего уровня

Индексный метод анализа динамики предполагает наличие системы взаимосвязанных индексов, в которой:

индекс переменного состава = индекс фиксированного состава индекс структурных сдвигов,
где индекс переменного состава отражает изменение среднего уровня показателя за счет двух факторов:

1) изменение качественного показателя;

2) изменение удельных весов, т.е. структуры совокупности.

Индекс фиксированного состава выявляет влияние качественного показателя, I структурных сдвигов характеризует динамику среднего показателя за счет изменений в структуре совокупности.

Из формулы средней

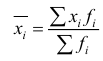следует,

что на среднюю величину оказывает влияние как значение осредняемого признака 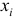, так и численность отдельных вариантов изучаемой совокупности.

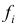Так, на среднюю цену овощей, продаваемых на рынках, влияют как различия индивидуальных цен, так и изменения объема реализации. Поэтому при анализе изменения цен важно определить, в какой мере это вызвано изменениями индексируемых величин и в какой – структурными сдвигами количества реализованной продукции. \

Таким образом, получаем, что общий индекс средней величины (индекс переменного состава) строится по формуле:

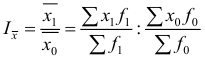
Индекс, характеризующий изменения средней величины вследствие изменений величин осредняемого признака у отдельных единиц совокупности – индекс постоянного (фиксированного) состава:

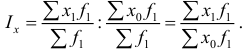
Индекс, характеризующий изменения средней величины вследствие изменений в структуре совокупности – индекс структурных сдвигов:

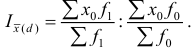
Получим систему взаимосвязанных индексов средней величины:

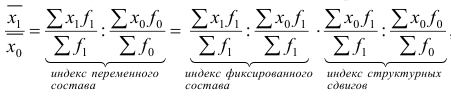
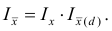
Можно вычислять эти же индексы, используя удельные веса, т.е. 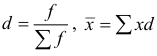. Тогда получим следующие формулы:

Индекс переменного состава: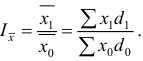

Индекс постоянного состава: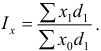

Индекс структурных сдвигов: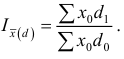

Пример оформления заказа №13.

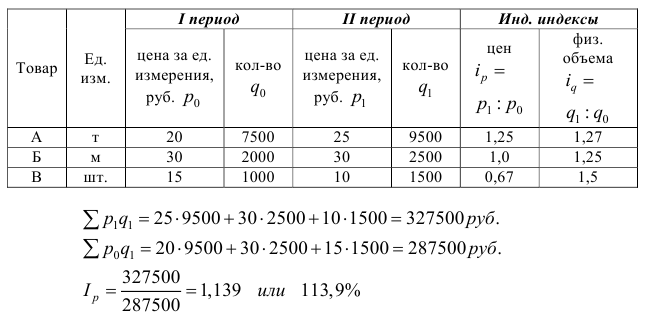
При сравнении числителя и знаменателя формулы в разности определяется показатель абсолютного прироста товарооборота за счет фактора изменения цен в текущем периоде по равнению с базисным периодом:

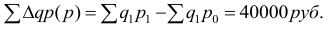
Полученная величина прироста говорит о том, что повышение цен на данный ассортимент товаров в среднем на 13,9% обусловило увеличение объема товарооборота в текущем периоде на 40 тыс.руб. Величина этого показателя (с противоположным знаком, т. е. – 40 тыс. руб.) характеризует перерасход денежных средств населением при покупке товаров данного ассортимента по ценам, повышенным на 13,9%.

Вычислим то же по формуле Ласпейреса:

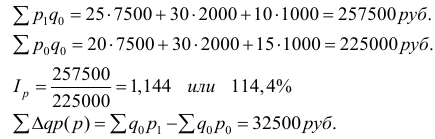
Полученная сумма прироста товарооборота показывает, что повышение цен в текущем периоде в среднем на 14,4% обусловливает увеличение объема товарооборота на 32,5 тыс. руб.

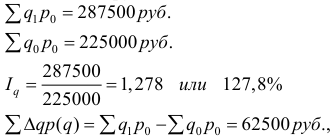
т. е. в результате изменения физического объема реализации товаров в текущем периоде получен прирост объема товарооборота в сопоставимых ценах на 62,5 тыс. руб.

Агрегатный индекс физического объема товарооборота может определяться посредством использования в качестве соизмерителя индексируемых величин 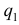и 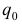цен текущего периода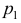

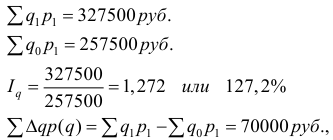
т. е. применение формулы (7) показывает, что по данному ассортименту реализованных в текущем периоде товаров прирост физического объема товарооборота составил 27,2%. Общий индекс товарооборота в текущих ценах составляет: 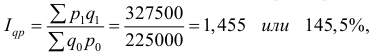т.е. в текущем периоде товарооборот в фактических ценах возрос по данному ассортименту товаров по сравнению с базисным периодом в среднем на 45,5%.