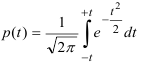Контрольные работы по статистике

Слово статистика происходит от латинского слова status, что в Средние века означало «политическое состояние вещей». В науку этот термин был введен немецким ученым Готфридом Ахенвалем (1719— 1772), и означал он тогда «государствоведение».

Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!

Статистика

В науку термин «статистика» (от лат. status – состояние, положение вещей; первоначально термин употреблялся в значении «политическое состояние») ввел немецкий ученый Готфрид Ахенваль в 1746 году, заменив название курса «Государствоведение», преподававшегося в университетах Германии, на «Статистику», положив тем самым начало развитию статистики как науки и учебной дисциплины. Несмотря на это, статистический учет велся намного раньше: проводились переписи населения в Древнем Китае, осуществлялось сравнение военного потенциала государств, велся учет имущества граждан в Древнем Риме и пр.

У истоков статистической науки стояли 2 школы: немецкая описательная и английская школа политических арифметиков. Представители описательной школы (Конринг, Ахенваль, Шленцер) своей задачей считали описание достопримечательностей государства: территории, населения, климата, политического устройства, вероисповедания, торговли и т.п. – без анализа закономерностей и связей между явлениями. Представители школы политических арифметиков (Уильям Петти, Граунт, Галлей) своей главной задачей считали выявление на основе большого числа наблюдений различных закономерностей и взаимосвязей в изучаемых явлениях. Каждая школа развивалась своим путем, используя свои методы в исследованиях, но предмет изучения у них был общий – государство, общество и, в частности, массовые явления и процессы, происходящие в нем. Статистика сформировалась как наука в результате синтеза государствоведения и политической арифметики, причем от последней она взяла больше, поскольку статистика и в настоящее время призвана выявлять прежде всего различного рода закономерности в исследуемых явлениях.

Однако представители этих двух школ не дошли до теоретического обобщения практики учетностатистических работ, до создания теории статистики. Эта задача была решена позднее, в XIX веке бельгийским ученым Адольфом Кетле, который дал определение предмета статистики, раскрыл суть ее методов. Под влиянием идей Кетле возникло третье направление статистической науки – математикостатистическое, которое получило свое развитие в работах таких ученых как: англичане Гальтон, Пирсон, Госсет, Фишер, русские – Чебышёв, Марков, Ляпунов, Чупров и пр.

Возможно эта страница вам будет полезна:

Предмет статистики

В настоящее время данный термин употребляется в 4 значениях:

1) наука, изучающая количественную сторону массовых явлений и процессов в неразрывной связи с их качественным содержанием – учебный предмет в высших и средних специальных учебных заведений;

2) совокупность цифровых сведений, характеризующих состояние массовых явлений и процессов общественной жизни; статистические данные, представляемые в отчетности предприятий, организаций, отраслей экономики, а также публикуемых в сборниках, справочниках, периодической печати и в сети Интернет, которые являются результатом статистической работы;

3) отрасль практической деятельности («статистический учет») по сбору, обработке, анализу и публикации массовых цифровых данных о самых различных явлениях и процессах общественной жизни (*эту деятельность на профессиональном уровне осуществляет государственная статистика – Федеральная служба государственной статистики (ФСГС) и система ее учреждений, организованных по административно-территориальному признаку, а также ведомственная статистика (на предприятиях, ведомствах, министерствах и т.д.). Информация ФСГС публикуется в специадльных печатных изданиях, а также в сети Интернет: www.gks.ru (или www.fsgs.ru));

4) некий параметр ряда случайных величин, получаемый по определенному алгоритму из результатов наблюдений, например, статистические критерии (критические статистики), применяющиеся при проверке различных гипотез (предположительных утверждений) относительно природы или значений отдельных показателей исследуемых данных, особенностей их распределения и пр. (*термин «статистика» как параметр, как статистический критерий употребляется преимущественно в математической статистике, некоторые из них (χ2 , t и др.) рассмотрены в соответствующих темах данного курса лекций)

Как и любая другая наука, статистика имеет свой предмет и метод исследования. Статистика изучает количественную сторону массовых общественных явлений в неразрывной связи с их качественной стороной или содержанием, а также исследует количественное выражение закономерностей общественного развития в конкретных условиях места и времени. Такое изучение основывается на системе категорий и понятий, отражающих наиболее общие и существенные свойства, признаки, связи и отношения предметов и явлений объективного мира.

Рассмотрим основные понятия, используемые в статистике.

1. Статистическая совокупность – множество социально-экономических объектов или явлений общественной жизни, объединенных качественной основой, но отличающихся друг от друга отдельными признаками. Таковы, например, совокупность домохозяйств, семей, предприятий и т.п.

2. Единица совокупности – первичный элемент статистической совокупности, являющийся носителем признаков и основой ведущегося при обследовании счета.

3. Признак единицы совокупности – свойства единицы совокупности, которые различаются способами их измерения и другими особенностями, что дает основание для их классификации 1.

Таблица 1. Основная классификация признаков в статистике

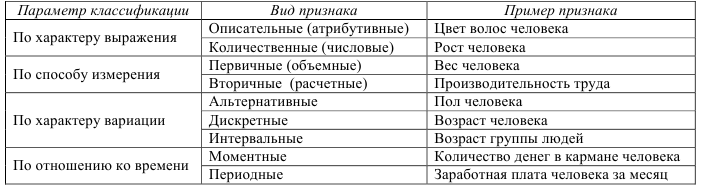
4. Статистический показатель – понятие, отображающее количественные характеристики (размеры) или соотношения признаков общественных явлений.

5. Система статистических показателей – совокупность статистических показателей, отражающая взаимосвязи, которые объективно существуют между явлениями.

Совокупность приемов, пользуясь которыми статистика исследует свой предмет, составляет метод статистики. Можно выделить 3 группы статистических методов (этапов статистического исследования): 1) статистическое наблюдение; 2) сводка (группировка) и 3) научный анализ исследуемых явлений.

Научно организованный сбор сведений, заключающийся в регистрации тех или иных фактов, признаков, относящихся к каждой единице изучаемой совокупности, называется статистическим наблюдением.

Обработка собранных первичных данных, включающая их группировку, обощение и оформление в таблицах, составляет второй этап статистического исследования, который называется сводкой. Существует 3 основных формы представления обработанных статистических данных: текстовая, табличная и графическая.

На третьем этапе статистического исследования на основе итоговых данных сводки осуществляется научный анализ исследуемых явлений: рассчитываются различные обобщающие показатели в виде средних и относительных величин, выявляются определенные закономерности в распределениях, динамике показателей и т.п. На основе выявленных закономерностей делаются прогнозы на будущее.

Люди по-разному относятся к статистической информации: одни не воспринимают ее, другие безоговорочно верят, а третьи согласны с мнением английского политика Дизраэли: «Существует 3 типа лжи: ложь, наглая ложь и статистика» , однако ему же принадлежит следующее утверждение: «В жизни, как правило, преуспевает больше тот, кто располагает лучшей информацией»

Абсолютные и относительные статистические величины

Абсолютные величины

Результаты статистических наблюдений представляют собой абсолютные величины, отражающие уровень развития какого-либо явления или процесса (например, величина экспорта/импорта i-го товара в j-ю страну). Абсолютные величины обозначаются X, а их общее количество в статистической совокупности N.

Абсолютные величины всегда имеют свою единицу измерения (размерность), присущую изучаемому явлению. Широко распространены следующие виды единиц измерения:

1) натуральные, подразделяющиеся на простые (например, штуки, тонны, метры) и сложные (составные), представляющие собой комбинацию двух разноименных величин (например, киловаттчас);
2) условно-натуральные (например, общая масса энергоносителей – дрова, торф, каменный уголь, нефтепродукты, природный газ – измеряется в т.у.т. – тонны условного топлива, поскольку каждый его вид имеет разную теплотворную способность, а за стандарт принято 29,3 МДж/кГ; общее количество школьных тетрадей измеряется в у.ш.т. – условные школьные тетради размером 12 листов; продукция консервного производства измеряется в у.к.б. – условные консервные банки емкостью 0,33 литра; продукция моющих средств приводится к условной жирности 40%.);
3) стоимостные, позволяющие соизмерить в денежной форме товары, которые нельзя соизмерить в натуральной форме (доллары США, рубли и т.д.).

Количество единиц с одинаковым значением признака обозначается f и называется частота (*f – это начальная буква англ. слова frequency – частота). Очевидно, что суммируя число всех единиц с одинаковыми значениями признака (*в статистике, в отличие от математики, пределы суммирования не ставятся, а подразумеваются, так как абсолютные величины здесь не абстрактные, а смысловые (суммируются все величины совокупности – с первой по последнюю)), получаем N, то есть (1):

Анализируя абсолютные величины, например, статистические данные о торговле, необходимо сопоставлять эти данные во времени и пространстве, исследовать закономерности их изменения и развития, изучать структуру совокупностей. С помощью абсолютных величин эти задачи не выполнимы, в этом случае необходимо использовать относительные величины.

Относительные величины

Относительная величина – это результат деления (сравнения) двух абсолютных величин. В числителе дроби стоит величина, которую сравнивают, а в знаменателе – величина, с которой сравнивают (база сравнения). Например, если сопоставить величины экспорта США и России, которые в 2005 году составили 904,383 и 243,569 млрд. долл. соответственно, то относительная величина покажет, что величина экспорта США в 3,71 раза (904,383/243,569) больше экспорта России, при этом базой сравнения является величина экспорта России. Полученная относительная величина выражена в виде коэффициента, который показывает, во сколько раз сравниваемая абсолютная величина больше базисной. В данном примере база сравнения принята за единицу. В случае если основание принимается за 100, относительная величина выражается в процентах (%), если за 1000 – в промилле (‰). Выбор той или иной формы относительной величины зависит от ее абсолютного значения:

– если сравниваемая величина больше базы сравнения в 2 раза и более, то выбирают форму коэффициента (как в вышеприведенном примере);
– если относительная величина близка к единице, то, как правило, ее выражают в процентах (например, сравнив величины экспорта России в 2006 и 2005 годах, которые составили 304,5 и 243,6 млрд. долл. соответственно, можно сказать, что экспорт в 2006 году составляет 125% от 2005 года [304,5/243,6*100%]);
– если относительная величина значительно меньше единицы (близка к нулю), ее выражают в промилле (например, в 2004 году Россия экспортировала в страны-СНГ всего 4142 тыс. т нефтепродуктов, в том числе в Грузию 10,7 тыс. т, что составляет 0,0026 [10,7/4142], или 2,6‰ от всего экспорта нефтепродуктов в страны СНГ).

Различают относительные величины динамики, структуры, координации, сравнения и интенсивности, для краткости именуемые в дальнейшем индексами.

Индекс динамики (*во многих учебниках по статистике встречается другое название индекса динамики – темп роста. Использование такого названия не совсем логично, так динамика может быть различна (не только рост, но и спад, а также стабильность), поэтому наиболее правильным является использование названия «индекс динамики» или «индекс изменения» где цифры означают: 1 – отчетный или анализируемый период, 0 – прошлый или базисный период) характеризует изменение какого-либо явления во времени. Он представляет собой отношение значений одной и той же абсолютной величины в разные периоды времени. Данный индекс определяется по формуле (2):

Критериальным значением индекса динамики служит единица (или 100%), то есть если 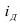>1, то имеет место рост (увеличение) явления во времени; если 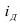=1 – стабильность; если 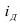<1 – наблюдается спад (уменьшение) явления. Еще одно название индекса динамики – индекс изменения, вычитая из которого единицу (100%), получают темп изменения (динамики) (*часто встречается и другое название темпа изменения – темп прироста, что не совсем логично) с критериальным значением 0, который определяется по формуле (3):

Если T>0, то имеет место рост явления; Т=0 – стабильность, Т<0 – спад.

В рассмотренном выше примере про экспорт России в 2006 и 2005 году был рассчитан именно индекс динамики по формуле (2): 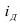= 304,5/243,6*100% = 125%, что больше критериального значения 100%, что свидетельствует об увеличении экспорта. Используя формулу (3) получим темп изменения: Т = 125% – 100% = 25%, который показывает, что экспорт увеличился на 25%.

Разновидностями индекса динамики являются индексы планового задания и выполнения плана, рассчитываемые для планирования различных величин и контроля их выполнения.

Индекс планового задания – это отношение планового значения признака к базисному. Он определяется по формуле (4):

где 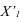– планируемое значение; 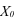– базисное значение признака.

Например, таможенное управление перечислило в федеральный бюджет в 2006 году 160 млрд.руб., а на следующий год запланировали перечислить 200 млрд.руб., значит по формуле (4): 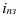= 200/160 = 1,25, то есть плановое задание для таможенного управления на 2007 год составляет 125% от предыдущего года.

Для определения процента выполнения плана необходимо рассчитать индекс выполнения плана, то есть отношение наблюдаемого значения признака к плановому (оптимальному, максимально возможному) значению по формуле (5):

Например, на январь-ноябрь 2006 года таможенные органы запланировали перечислить в федеральный бюджет 1,955 трлн. руб., но фактически перечислили 2,59 трлн. руб., значит по формуле (5): 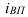= 2,59/1,955 = 1,325, или 132,5%, то есть плановое задание выполнили на 132,5%.

Индекс структуры (доля) – это отношение какой-либо части объекта (совокупности) ко всему объекту. Он определяется по формуле (6):

В рассмотренном выше примере про экспорт нефтепродуктов в страны СНГ, была рассчитана доля этого экспорта в Грузию по формуле (6): d=10,7/4142 = 0,0026, или 2,6‰.

Индекс координации – это отношение какой-либо части объекта к другой его части, принятой за основу (базу сравнения). Он определяется по формуле (7):

Например, импорт России в 2006 году составил 163,9 млрд.долл., тогда, сравнив его с экспортом (база сравнения), рассчитаем индекс координации по формуле (7): 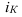= 163,9/304,5 = 0,538, который показывает соотношение между двумя составными частями внешнеторгового оборота, то есть величина импорта России в 2006 году составляет 53,8% от величины экспорта. Меняя базу сравнения на импорт, по той же формуле получим: 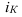= 304,5/163,9 = 1,858, то есть экспорт России в 2006 году в 1,858 раза больше импорта, или экспорт составляет 185,8% от импорта.

Индекс сравнения – это сравнение (соотношение) разных объектов по одинаковым признакам. Он определяется по формуле (8):

где А, Б – сравниваемые объекты.

В рассмотренном выше примере, в котором сопоставлялись величины экспорта США и России, был рассчитан именно индекс сравнения по формуле (8): 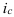= 904,383/243,569 = 3,71. Меняя базу сравнения (то есть экспорт России – объект А, а экспорт США – объект Б), по той же формуле получим: 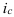= 243,569/904,383 = 0,27, то есть экспорт России составляет 27% от экспорта США.

Индекс интенсивности – это соотношение разных признаков одного объекта между собой. Он определяется по формуле (9):

где X – один признак объекта; Y – другой признак этого же объекта

Например, показатели выработки продукции в единицу рабочего времени, затрат на единицу продукции, цены единицы продукции и т.д.

Контрольная работа 1.

Перевести в тонны условного топлива 23,8 млн. т. нефти с теплотворной способностью 45 Мдж/кГ.

Решение:

Учитывая стандартную теплотворную способность 29,3 МДж/кГ, определяем: 23,8*45/29,3 = 36,55 млн. т.у.т.

Контрольная работа 2.

Рассчитать индекс и темп изменения, если в марте произведено продукции 138 тонн, а в феврале 108 тонн.

Решение:

Индекс изменения (динамики) по формуле (2): 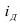= 138/108 = 1,278 или 127,8% — рост, т.к. 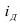> 1. 2.2. Темп изменения по формуле (3): T = 1,278 – 1 = 0,278 или 27,8% — рост, т.к. 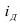> 0.

Контрольная работа 3.

Рассчитать индексы планового задания, выполнения плана и динамики, если выпуск продукции в отчетном году составил 20 млн.рублей. На следующий год планировалось 28 млн.рублей, а фактически получено 26 млн.рублей.

Решение:

Индекс планового задания по формуле (4): 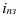= 28/20 = 1,4.
3.2. Индекс выполнения плана по формуле (5): 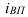= 26/28 = 0,928. 3.3. Индекс динамики по формуле (2) 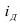= 26/20 = 1,3 или 130% — рост, т.к. 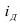> 1.

Контрольная работа 4.

В составе ВВП региона 136,5 млр.рублей произведено товаров на 75,4 млр.рублей, оказано услуг на 51,6 млр.рублей и собрано налогов 9,5 млр.рублей. Рассчитать относительные величины структуры и координации, приняв за основу производство товаров.

Решение:

Индексы структуры (доли) по формуле (6): товары 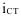= 75,4/136,5 = 0,552 или 55,2%; услуги 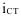= 51,6/136,5 = 0,378 или 37,8%; налоги 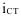= 9,5/136,5 = 0,07 или 7%. Контроль: 0,552 + 0,378 + 0,07 = 1.
4.2. Индексы координации по формуле (7): услуги 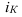= 51,6/75,4 =0,684; налоги 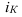= 9,5/75,4 = 0,126.

Контрольная работа 5.

Запасы воды в озере Байкал составляют 23000 км3 , а в Ладожском озере 911 км3 . Рассчитать относительные величины сравнения этих озер.

Решение:

Индекс сравнения озер Байкал с Ладожским по формуле (8): 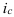= 23000/911 = 25,25. 5.2. Индекс сравнения Ладожского озера с Байкалом по той же формуле: 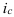= 911/23000 = 0,0396 или 1/25,25 = 0,0396.

Контрольная работа 6.

Рассчитать относительную величину интенсивности ВВП в сумме 276611 млн.$ на душу населения в 147 млн.человек.

Решение:

Показатель интенсивности по формуле (9) 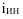= 276611/147 = 1881,7 $/чел.

Средние величины и показатели вариации, понятие средней величины

Статистическая совокупность содержит некоторое количество статистических величин, имеющих, как правило, разные значения и признаки, что делает невозможным сравнение нескольких совокупностей в целом. Для этой цели применяется средняя величина, как обобщающий показатель совокупности, характеризующий уровень изучаемого явления или процесса.

Средняя величина всегда обобщает количественное выражение признака и погашает индивидуальные различия статистических величин совокупности, вызванные случайными обстоятельствами. Но по значению средней величины нельзя делать принципиальные выводы. Например, если один ученик имеет тетрадь в 48 листов, а другой — ни одной, то в среднем получается по 2 у.ш.т. на ученика. Но из этого нельзя заключать, что все ученики школьными тетрадями обеспечены.

Главное значение средних величин состоит в их обобщающей функции, то есть замене множества различных индивидуальных значений признака средней величиной, характеризующей всю совокупность явлений.

Виды средних величин

Виды средних величин различаются прежде всего тем, какое свойство, какой параметр исходной варьирующей массы индивидуальных значений признака должен быть сохранен неизменным.

Средней арифметической величиной называется такое среднее значение признака, при вычислении которого общий объем признака в совокупности сохраняется неизменным. Иначе можно сказать, что средняя арифметическая величина – среднее слагаемое. При ее вычислении общий объем признака мысленно распределяется поровну между всеми единицами совокупности. Исходя из определения, формула средней арифметической величины имеет вид (10):

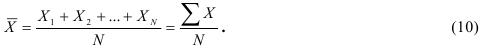
По формуле (10) вычисляются средние величины первичных признаков, если известны индивидуальные значения признака. Если изучаемая совокупность велика, исходная информация чаще представляет собой ряд распределения или группировку, как, например, табл. 2.

Таблица 2. Распределение студентов группы дневного отделения по возрасту

Средний возраст должен представлять собой результат равномерного распределения общего (суммарного) возраста всех студентов. Общий (суммарный) возраст всех студентов, согласно исходной информации табл. 2, можно получить как сумму произведений значений признака в каждой группе 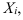на число студентов с таким возрастом 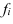(частоты). Получим формулу (11):

где i – число групп.

Такую форму средней арифметической величины называют взвешенной арифметической средней (*обычно в статистических формулах пределы суммирования не ставятся, а подразумеваются, т.е. подразумеваются именно такие пределы как формуле (11) – с 1-ой группы по N-ю (последнюю)) в отличие от простой средней, рассчитанной по формуле (10). В качестве весов здесь выступают количество единиц совокупности в разных группах. Название «вес» выражает тот факт, что разные значения признака имеют неодинаковую «важность» при расчете средней величины. «Важнее», весомее возраст студентов 18, 19, 20 лет, а такие значения возраста как 17, 20 или 21 при расчете средней не играют большой роли – их «вес» мал.

По формуле (11) по данным табл. 2 имеем:

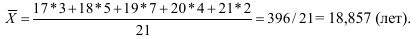
Как видим, средняя арифметическая величина может быть дробным числом, если даже индивидуальные значения признака могут принимать только целые значения. Ничего необычного для метода средних в этом не заключено, так как из сущности средней не следует, что она обязана быть реальным значением признака, которое могло бы встретиться у какой-либо единицы совокупности.

Если при группировке значения осредняемого признака заданы интервалами, то при расчете средней арифметической величины в качестве значения признака в группах принимают середины этих интервалов, то есть исходят из предположения о равномерном распределении единиц совокупности по интервалу значений признака. Для открытых интервалов в первой и последней группе, если таковые есть, значения признака надо определить экспертным путем исходя из сущности, свойств признака и совокупности. При отсутствии возможности экспертной оценки значения признака в открытых интервалах, для нахождения недостающей границы открытого интервала применяют размах (разность между значениями конца и начала интервала) соседнего интервала (принцип «соседа»).

Например, по данным табл. 3 можно минимальную и максимальную величину веса студентов определить затруднительно, поэтому воспользуемся принципом «соседа» – применим размах соседнего интервала, который у второго и предпоследнего составляет 10 кг, значит первый интервал будет от 55 до 65 кг, а последний – от 80 до 90 кг. Середины интервалов определяем как полусумму нижней и верхней границы интервалов.

Таблица 3. Распределение группы студентов по весу

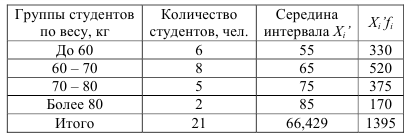
Средняя вес студентов, рассчитанный по формуле (11) с заменой точных значений признака в группах серединами интервалов, составил:

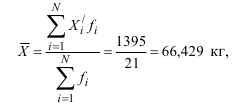
что и записано в итоговую строку в 3-м столбце табл. 3. Следует обратить внимание, что объемного показателя – это сумма, а итог по столбцам относительных показателей или средних групповых величин – средняя.

Средняя арифметическая величина обладает свойствами, знание которых полезно как при ее использовании, так и при ее расчете.

1) Сумма отклонений индивидуальных значений признака от его среднего значения равна нулю.
2) Если каждое индивидуальное значение признака умножить или разделить на постоянное число, то и средняя увеличится или уменьшится во столько же раз. Вследствие этого свойства индивидуальные значения признака можно сократить в c раз, произвести расчет средней и результат умножить на c.
3) Если к каждому индивидуальному значению признака прибавить или из каждого значения вычесть постоянное число, то средняя величина возрастет или уменьшится на это же число. Это свойство полезно использовать при расчете средней величины из многозначных и слабоварьирующих значений признака аналогично предыдущему свойству.
4) Если веса средней взвешенной умножить или разделить на постоянное число, средняя величина не изменится. Используя это свойство, при расчетах следует сокращать веса на их общий сомножитель либо выражать многозначные числа весов в более крупных единицах измерениях.
5) Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем от любого другого числа.

Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменную сумму квадратов исходных величин, то средняя будет являться квадратической средней величиной. Ее формула следующая:

Главной сферой применения квадратической средней в силу пятого свойства средней арифметической величины является измерение вариации признака в совокупности.

Аналогично, если по условиям задачи необходимо сохранить неизменной сумму кубов индивидуальных значений признака при их замене на среднюю величину, мы приходим к средней кубической величине, имеющей вид:

Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменным произведение индивидуальных величин, то следует применить геометрическую среднюю величину, имеющую следующий вид:

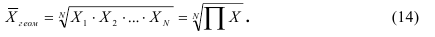
Основное применение средняя геометрическая находит при определении средних относительных изменений, о чем сказано в теме «Ряды динамики». Геометрическая средняя величина дает наиболее точный результат осреднения, если задача также состоит в нахождении такого значения признака, который качественно был бы равноудален как от максимального, так и от минимального значения признака.

Когда статистическая информация не содержит частот f по отдельным вариантам 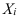совокупности, а представлена как их произведение тогда применяется формула средней гармонической взвешенной, для получения которой обозначим Xf=w, откуда f=w/X, и, подставив эти обозначения в формулу (11), получим формулу (15):

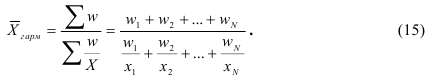
Таким образом, средняя гармоническая взвешенная применяется тогда, когда неизвестны действительные веса f, а известно w=Xf. В тех случаях, когда вес каждого варианта w=1, то есть индивидуальные значения X встречаются по 1 разу, применяется формула средней гармонической простой (16):

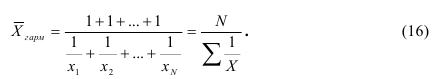
Все рассмотренные выше виды средних величин принадлежат к общему типу степенных средних, имеющему следующий вид:

При m = 1 получаем среднюю арифметическую; при m = 2 – среднюю квадратическую; при m = 3 – среднюю кубическую; при m = 0 – среднюю геометрическую; при m = –1 – среднюю гармоническую. Чем выше показатель степени m, тем больше значение средней величины (если индивидуальные значения признака варьируют). В итоге, можно построить следующее соотношение, которое называется правилом мажорантности средних:

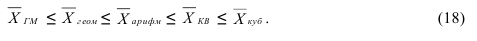
Возможно эта страница вам будет полезна:

Примеры решения задач по статистике

Статистическое изучение вариации

Признаки, изучаемые статистикой, варьируются (отличаются друг от друга) у различных единиц совокупности в один и тот же период или момент времени. Например, величина внешнеторгового оборота (ВО) варьируется по подразделениям Федеральной таможенной службы; величина экспорта (импорта) варьируется по направлениям экспорта (по разным странам-партнерам по внешней торговле), по видам товаров и т.п.

Причиной вариации являются разные условия существования разных единиц совокупности.

Например, огромное число причин влияет на масштабы внешней торговли различных стран мира.

Для управления и изучения вариации статистикой разработаны специальные методы исследования вариации, система показателей, с помощью которой вариация измеряется, характеризуются ее свойства.

Первым этапом статистического изучения вариации является построение ряда распределения (или вариационного ряда) – упорядоченного распределения единиц совокупности по возрастающим (чаще) или по убывающим (реже) значениям признака и подсчет числа единиц с тем или иным значением признака.

Существует 3 вида ряда распределения:

1) ранжированный ряд – это перечень отдельных единиц совокупности в порядке возрастания изучаемого признака (например, таблица 4); если численность единиц совокупности достаточно велика ранжированный ряд становится громоздким, и в таких случаях ряд распределения строится с помощью группировки единиц совокупности по значениям изучаемого признака (ели признак принимает небольшое число значений, то строится дискретный ряд, а в противном случае – интервальный ряд);

2) дискретный ряд – это таблица, состоящая из двух столбцов (строк) – конкретных значений варьирующего признака 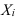и числа единиц совокупности с данным значением признака 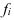– частот; число групп в дискретном ряду определяется числом реально существующих значений варьирующего признака;

3) интервальный ряд – это таблица, состоящая из двух столбцов (строк) – интервалов варьирующего признака 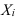и числа единиц совокупности, попадающих в данный интервал (частот), или долей этого числа в общей численности совокупностей (частостей).

Построим ряд распределения внешнеторгового оборота (ВО) по таможенным постам России, для чего необходимо провести статистическое наблюдение, то есть собрать первичный статистический материал, который представляет собой величину ВО по таможенным постам.

Результаты наблюдения ВО по 35 таможенным постам региона за отчетный период представим в виде ранжированного по возрастанию величины ВО ряда распределения (таблица 4).

Таблица 4. Внешнеторговый оборот (ВО) по 35 таможенным постам, млн.долл.

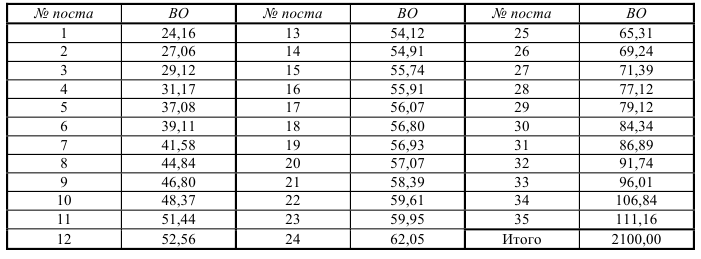
Построим интервальный ряд распределения ВО по таможенным постам, для чего необходимо выбрать оптимальное число групп (интервалов признака) и установить длину (размах) интервала. Поскольку при анализе ряда распределения сравнивают частоты в разных интервалах, необходимо, чтобы длина интервалов была постоянной (*если приходится иметь дело с интервальным рядом распределения с неравными интервалами, то для сопоставимости нужно частоты или частости привести к единице интервала, полученное значение называется плотностью ρ, то есть ρ = f/h). Оптимальное число групп выбирается так, чтобы достаточной мере отразилось разнообразие значений признака в совокупности и в то же время закономерность распределении, его форма не искажалась случайными колебаниями частот. Если групп будет слишком мало, не проявится закономерность вариации; если групп будет чрезмерно много, случайные скачки частот исказят форму распределения.

Чаще всего число групп в ряду распределения определяют по формуле Стерждесса (19) или (20):

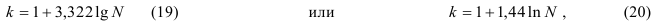
где k – число групп (округляемое до ближайшего целого числа); N – численность совокупности.

Из формулы Стерджесса видно, что число групп – функция объема данных (N). Зная число групп, рассчитывают длину (размах) интервала (*единицы совокупности, имеющие значение признака, равное границе интервала, включаются в тот интервал, где это точное значение впервые указывается) по формуле (21):

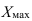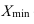где и — максимальное и минимальное значения в совокупности.

В нашем примере про ВО по формуле Стерждесса (19) определим число групп:
k = 1 + 3,322lg35 = 1+ 3,322*1,544 = 6,129 ≈ 6.
Рассчитаем длину (размах) интервала по формуле (21):
h = (111,16 – 24,16)/6 = 87/6 = 14,5 (млн.долл.).

Теперь построим интервальный ряд с 6 группами с интервалом 14,5 млн.долл. (см. первые 3 столбца табл. 5).

Таблица 5. Интервальный ряд распределения ВО по таможенным постам, млн.долл.

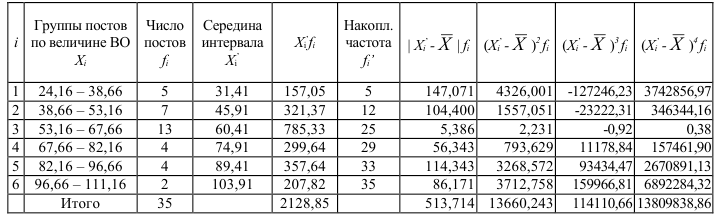
Существенную помощь в анализе ряда распределения и его свойств оказывает графическое изображение. Интервальный ряд изображается столбиковой диаграммой, в которой основания столбиков, расположенные по оси абсцисс, – это интервалы значений варьирующего признака, а высоты столбиков – частоты, соответствующие масштабу по оси ординат. Графическое изображение распределения таможенных постов в выборке по величине ВО приведено на рис. 1. Диаграмма такого типа называется гистограммой (*от греч. «гистос» – ткань, строение) .

Данные табл. 5 и рис. 1 показывают характерную для многих признаков форму распределения: чаще встречаются значения средних интервалов признака, реже – крайние (малые и большие) значения признака. Форма этого распределения близка к нормальному закону распределения, которое образуется, если на варьирующую переменную влияет большое число факторов, ни один из которых не имеет преобладающего значения.

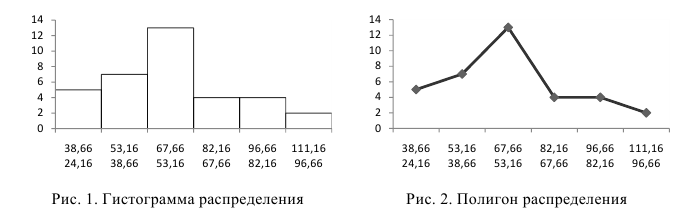
Если имеется дискретный ряд распределения или используются середины интервалов (как в нашем примере про ВО – в таблице 5 в 4-м столбце рассчитаны середины интервалов как полусумма значений начала и конца интервала), то графическое изображение такого ряда называется полигоном (см. рис. 2)(*от греч. слов «поли» и «гонос» – многоугольник) , которое получается соединением прямыми точек с координатам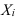и и .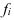

Вторым этапом статистического изучения вариации является расчет характеристик ряда распределения, которые описывают количественно его структуру, строение. Такова, например, медиана – величина варьирующего признака, делящая совокупность на две равные части – со значением признака меньше медианы и со значением признака больше медианы (*при четном числе единиц совокупности за медиану принимают полусумму из двух центральных вариант). В нашем примере про ВО (табл. 4) медиана – это 18-й таможенный пост из 35 с величиной ВО 56,8 млн.долл. Из этого примера видно принципиальное различие между медианой и средней величиной: медиана не зависит от значений на краях ранжированного ряда. Даже если бы ВО 35-го таможенного поста был в 10 раз больше, величина медианы не изменилась бы. Поэтому медиану часто используют как более надежный показатель типичного значения признака, нежели средняя арифметическая, если ряд значений неоднороден, включает резкие отклонения от средней. В интервальном ряду распределения для нахождения медианы применяется формула:

где Ме – медиана;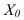
– нижняя граница интервала, в котором находится медиана;
h – величина (размах) интервала;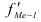
– накопленная частота в интервале, предшествующем медианному;
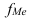– частота в медианном интервале.

В табл. 5 медианным является среднее из 35 значений, т.е. 18-е от начала значение ВО. Как видно из столбца накопленных частот (6-й столбец), оно находится в третьем интервале. Тогда по формуле (22):

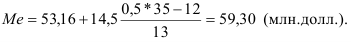
Аналогично медиане вычисляются значения признака, делящие совокупность на 4 равные по численности части – квартили, которые обозначаются заглавной латинской буквой Q с подписным значком номера квартиля. Ясно, что 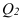совпадает с Ме. Для первого и третьего квартилей приводим формулы и расчет по данным табл. 5:

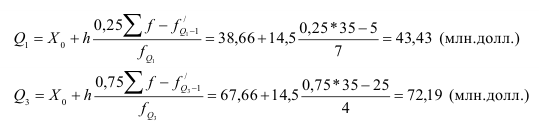
Так как 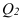= Ме = 59,30 млн.долл., видно, что различие между первым квартилем и медианой (–15,87) больше, чем между медианой и третьим квартилем (12,89). Этот факт свидетельствует о наличии некоторой несимметричности в средней области распределения, что заметно и на рис. 1.

Значения признака, делящие ряд на 5 равных частей, называются квинтилями, на 10 частей – децилями, на 100 частей – перцентилями. Эти характеристики применяются при необходимости подробного изучения структуры ряда распределения.

Безусловно, важное значение имеет такая величина признака, которая встречается в изучаемом ряду распределения чаще всего. Такую величину принято называть модой. В дискретном ряду мода определяется без вычисления как значение признака с наибольшей частотой. Обычно встречаются ряды с одним модальным значением признака. Если в ряду распределения встречаются 2 или несколько равных (и даже несколько различных, но больших чем соседние) значений признака, то он считается соответственно бимодальным или мультимодальным. Это свидетельствует о неоднородности совокупности, возможно, представляющей собой агрегат нескольких совокупностей с разными модами.

В интервальном ряду распределения интервал с наибольшей частотой является модальным. Внутри этого интервала находят условное значение признака, вблизи которого плотность распределения (число единиц совокупности, приходящихся на единицу измерения варьирующего признака) достигает максимума. Это условное значение и считается точечной модой. Логично предположить, что такая точечная мода располагается ближе к той из границ интервала, за которой частота в соседнем интервале больше частоты в интервале за другой границей модального интервала. Отсюда получаем обычно применяемую формулу (23):

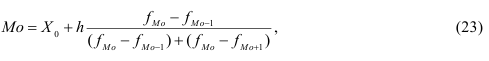
где Мо – мода;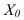
– нижнее значение модального интервала;
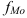– частота в модальном интервале;
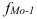– частота в предыдущем интервале;
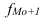– частота в следующем интервале за модальным;
h – величина интервала.

По данным табл. 5 рассчитаем точечную моду по формуле (23):

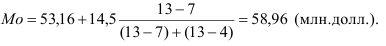
К изучению структуры ряда распределения средняя арифметическая величина также имеет отношение, хотя основное значение этого обобщающего показателя другое. В интервальном ряду распределения ВО по таможенным постам средняя арифметическая рассчитывается как взвешенная по частоте середина интервалов X (расчет числителя – в 5-м столбце табл. 5) по формуле (11):

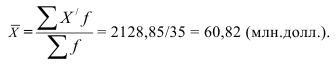
Различие между средней арифметической величиной (60,82), медианой (59,30) и модой (58,96) в нашем примере невелико. Чем ближе распределение по форме к нормальному закону, тем ближе значения медианы, моды и средней величины между собой.

Третьим этапом статистического изучения вариации является расчет показателей размера и интенсивности вариации. Простейшим показателем является размах вариации – абсолютная разность между максимальным и минимальным значениями признака из имеющихся в изучаемой совокупности значений (24):

Поскольку величина размаха характеризует лишь максимальное различие значений признака, она не может измерять закономерную силу его вариации во всей совокупности. Предназначенный для данной цели показатель должен учитывать и обобщать все различия значений признака в совокупности без исключения. Число таких различий равно числу сочетаний по два из всех единиц совокупности (в нашем примере про ВО число сочетаний составит 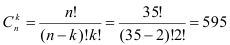). Однако нет необходимости рассматривать, вычислять и осреднять все отклонения. Проще использовать среднюю из отклонений отдельных значений признака от среднего арифметического значения признака, а таковых в нашем примере про ВО всего 35. Но среднее отклонение значений признака от средней арифметической величины согласно первому свойству последней равно нулю. Поэтому показателем силы вариации выступает не арифметическая средняя отклонений, а средний модуль отклонений, или среднее линейное отклонение (25):

В нашем примере про ВО по данным табл. 5 среднее линейное отклонение вычисляется как взвешенное по частоте отклонение по модулю середин интервалов от средней арифметической величины (расчет числителя произведен в 7-м столбце табл. 5), т.е. по формуле (26):

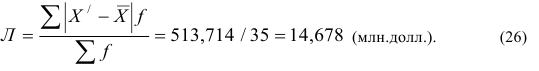
Это означает, что в среднем величина ВО в изучаемой совокупности таможенных постов отклонялась от средней величины ВО в РФ на 14,678 млн.долл.

Простота расчета и интерпретации составляют положительные стороны показателя Л, однако математические свойства модулей «плохие»: их нельзя поставить в соответствие с каким-либо вероятностным законом, в том числе и с нормальным распределением, параметром которого является не средний модуль отклонений, а среднее квадратическое отклонение, обозначаемое малой греческой буквой сигма ( 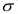) или s и вычисляемое по формуле (27) – для ранжированного ряда и по формуле (28) – для интервального ряда:

В нашем примере про ВО по данным табл. 5 среднее квадратическое отклонение величины ВО по формуле (28) составило (расчет числителя произведен в 8-м столбце табл. 5):

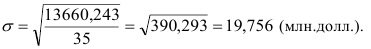
Среднее квадратическое отклонение по величине в реальных совокупностях всегда больше среднего модуля отклонений. Разница между ними тем больше, чем больше в изучаемой совокупности резких, выделяющихся отклонений, что служит индикатором «засоренности» совокупности неоднородными с основной массой элементами. Для нормального закона распределения отношение 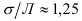. В нашем примере про ВО: 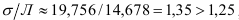, т.е. в изучаемой совокупности наблюдаются некоторое число таможенных постов с отличающимися от основной массы величинами ВО.

Квадрат среднего квадратического отклонения представляет собой дисперсию отклонений, на использовании которой основаны практически все методы математической статистики, ее формула имеет вид (29) – для несгруппированных данных (простая дисперсия) и (30) – для сгруппированных (взвешенная дисперсия):

Еще одним показателем силы вариации, характеризующим ее не по всей совокупности, а лишь в ее центральной части, служит среднее квартильное расстояние (отклонение), т.е. средняя величина разности между квартилями, определяемая по формуле (31):

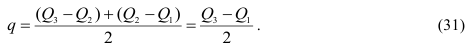
В нашем примере про ВО по формуле (31):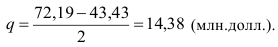

Сила вариации в центральной части совокупности, как правило, меньше, чем в целом по всей совокупности. Соотношение между средним линейным отклонением и средним квартильным расстоянием служит для изучения структуры вариации: большое значение такого соотношения свидетельствует о наличии слабоварьирующего «ядра» и сильно рассеянного вокруг него окружения в изучаемой совокупности. Для нашего примера про ВО соотношение Л/q = 1,021, что говорит о совсем незначительном различии силы вариации в центральной части совокупности и на ее периферии.

Для оценки интенсивности вариации и для сравнения ее в разных совокупностях и тем более для разных признаков необходимы относительные показатели вариации, которые вычисляются как отношение абсолютных показателей силы вариации, рассмотренных ранее, к средней арифметической величине признака, то есть показатели (32) – (35):

– относительный размах вариации: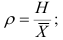(32)
– линейный коэффициент вариации: 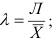(33)
– квадратический коэффициент вариации: 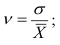(34)
– относительное квартильное расстояние: 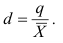(35)

В нашем примере про ВО эти показатели составляют:

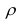= 87/60,82 =1,43, или 143%;
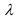= 14,678/60,82 = 0,241, или 24,1%;
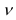= 19,756/60,82 = 0,32, или 32%;
d = 14,38/60,82 = 0,236, или 23,6%.

Оценка степени интенсивности вариации возможна только для каждого отдельного признака и совокупности определенного состава, она состоит в сравнении наблюдаемой вариации с некоторой обычной ее интенсивностью, принимаемой за норматив (максимально возможные значения показателей вариации: 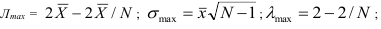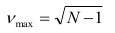). Так, для совокупности таможенных постов вариация величины ВО может быть определена как слабая, если 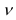< 25%, умеренная при 25% < 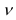< 50% и сильная при 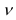> 50%.

Различная сила, интенсивность вариации обусловлены объективными причинами, поэтому нельзя говорить о каком-либо универсальном критерии вариации (например, 33%), так как для разных явлений и признаков этот критерий различен. Например, цена продажи американского доллара в коммерческих банках Н.Новгорода 26 июля 2007 года варьировала от 25,45 до 26,00 при средней цене 25,595 руб., тогда по формуле (32) 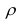= (26,00–25,45)/25,595 = 0,021, или 2,1%. Такая малая вариация вызвана тем, что при значительном различии курса доллара немедленно произошел бы отлив покупателей из «дорогого» банка в более «дешевые». Напротив, цена килограмма говядины в разных регионах России варьирует очень сильно – на десятки процентов и более (это объясняется разными затратами на доставку товара из региона-производителя в регион потребитель).

Возможно эта страница вам будет полезна:

Курсовая работа по статистике

Четвертым этапом статистического изучения вариации является расчет моментов распределения и показателей его формы. Для дальнейшего изучения характера вариации используются средние значения разных степеней отклонений отдельных величин признака от его средней арифметической величины. Эти показатели называются центральные моменты распределения порядка, соответствующего степени, в которую возводятся отклонения (табл. 6) или просто моментов (нецентральные моменты в таможенной статистике практически не используются).

Таблица 6. Центральные моменты

Величина третьего момента 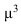зависит, как и его знак, от преобладания положительных кубов отклонений над отрицательными кубами либо наоборот. При нормальном и любом другом строго симметричном распределении сумма положительных кубов строго равна сумме отрицательных кубов, поэтому на основе третьего момента строится показатель, характеризующий степень асимметричности распределения – коэффициент асимметрии (36):

В нашем примере про ВО показатель асимметрии по формуле (36) составил (расчет числителя произведен в 9-м столбце табл. 5):

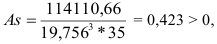т.е. асимметрия значительна.

Английский статистик К.Пирсон на основе разности между средней арифметической величиной и модой предложил другой показатель асимметрии (37):

В нашем примере по данным табл. 5 показатель асимметрии по формуле (37) составил:

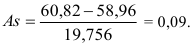
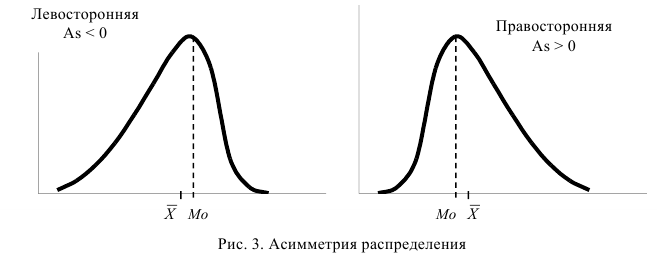
Показатель асимметрии Пирсона (37) зависит от степени асимметричности в средней части ряда распределения, а показатель асимметрии (36) – от крайних значений признака. Таким образом, в нашем примере про ВО в средней части распределения наблюдается меньшая асимметрия, чем по краям, что видно и по графику (рис. 2). Распределения с сильной правосторонней и левосторонней асимметрией показаны на рис. 3.

С помощью момента четвертого порядка характеризуется еще более сложное свойство рядов распределения – эксцесс (от англ. «излишество»). Показатель эксцесса рассчитывается по формуле (38):

Чаще всего эксцесс интерпретируется как «крутизна» распределения, что не совсем верно. График распределения может выглядеть сколь угодно крутым в зависимости от силы вариации признака: чем слабее вариация, тем круче кривая распределения при данном масштабе. Не говоря уже о том, что, изменяя масштабы по осям абсцисс и ординат, любое распределение можно искусственно сделать «крутым» и «пологим». Чтобы показать, в чем состоит эксцесс распределения, и правильно его интерпретировать, нужно сравнить ряды с одинаковой силой вариации (одной и той же величиной σ) и разными показателями эксцесса. Чтобы не смешать эксцесс с асимметрией, все сравниваемые ряды должны быть симметричными. Такое сравнение изображено на рис. 4.

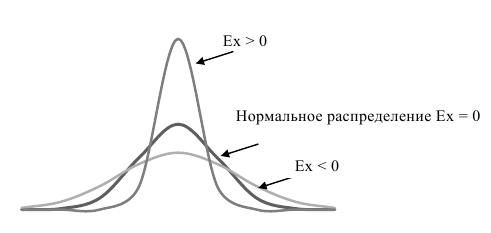
Рис. 4. Эксцесс распределения

Наличие положительного эксцесса означает наличие слабоварьирующего «ядра» и сильно рассеянного вокруг него окружения в изучаемой совокупности. Отрицательный эксцесс означает отсутствие такого «ядра».

В нашем примере по формуле (38) эксцесс составил (расчет числителя произведен в 10-м столбце табл. 5):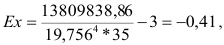т.е. величина ВО по таможенным постам варьирует сильнее, чем при нормальном распределении.

Пятым этапом статистического изучения вариации является проверка соответствия ряда распределения теоретическому (нормальному, логнормальному, биномиальному, распределению Руассона и др.) с помощью критериев согласия, среди которых чаще всего применяют критерии Пирсона 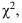Колмогорова и Романовского.

Выборочное наблюдение, понятие выборочного наблюдения

Выборочный метод используется, когда применение сплошного наблюдения физически невозможно из-за огромного массива данных или экономически нецелесообразно. Физическая невозможность имеет место, например, при изучении пассажиропотоков, рыночных цен, семейных бюджетов. Экономическая нецелесообразность имеет место при оценке качества товаров, связанной с их уничтожением. Например, дегустация, испытание кирпичей на прочность и т.п. Выборочное наблюдение используется также для проверки результатов сплошного.

Статистические единицы, отобранные для наблюдения, составляют выборочную совокупность или выборку, а весь их массив — генеральную совокупность (ГС). При этом число единиц в выборке обозначают п, во всей ГС – N. Отношение n/N называется относительный размер или доля выборки.

Качество результатов выборочного наблюдения зависит от репрезентативности выборки, т.е. от того, насколько она представительна в ГС. Для обеспечения репрезентативности выборки необходимо соблюдать принцип случайности отбора единиц, который предполагает, что на включение единицы ГС в выборку не может повлиять какой-либо иной фактор кроме случая.

Способы формирования выборки

1. Собственно случайный отбор: все единицы ГС нумеруются, а выпавшие в результате жеребьевки номера соответствуют единицам, попавшим в выборку, причем число номеров равно запланированному объему выборки. На практике вместо жеребьевки используют генераторы случайных чисел. Данный способ отбора может быть повторным (когда каждая единица, отобранная в выборку, после проведения наблюдения возвращается в ГС и может быть вновь подвергнута обследованию) и бесповторным (когда обследованные единицы в ГС не возвращаются и не могут быть обследованы повторно). При повторном отборе вероятность попадания в выборку для каждой единицы ГС остается неизменной, а при бесповторном отборе она меняется (увеличивается), но для оставшихся в ГС после отбора из нее нескольких единиц, вероятность попадания в выборку одинакова.

2. Механический отбор: отбираются единицы генеральной совокупности с постоянным шагом N/n. Так, если она генеральная совокупность содержит 100 тыс.ед., а требуется выбрать 1 тыс.ед., то в выборку попадет каждая сотая единица.

3. Стратифицированный (расслоенным) отбор осуществляется из неоднородной генеральной совокупности, когда ее предварительно разбивают на однородные группы, после чего производят отбор единиц из каждой группы в выборочную совокупность случайный или механическим способом пропорционально их численности в генеральной совокупности.

4. Серийный (гнездовой) отбор: случайным или механическим способом выбирают не отдельные единицы, а определенные серии (гнезда), внутри которых производится сплошное наблюдение.

Средняя ошибка выборки

После завершения отбора необходимого числа единиц в выборку и регистрации предусмотренных программой наблюдения изучаемых признаков этих единиц, переходят к расчету обобщающих показателей. К ним относят среднюю величину изучаемого признака и долю единиц, обладающих каким-либо значением этого признака. Однако, если ГС произвести несколько выборок, определив при этом их обобщающие характеристики, то можно установить, что их значения будут различными, кроме того, они будут отличаться и от реального их значения в ГС, если такое определить с помощью сплошного наблюдения. Другими словами, обобщающие характеристики, рассчитанные по данным выборки, будут отличаться от их реальных значений в ГС, поэтому введем следующие условные обозначения (табл. 7).

Таблица 7. Условные обозначения

Разность между значением обобщающих характеристик выборочной и генеральной совокупностей называется ошибкой выборки, которая подразделяется на ошибку регистрации и ошибку репрезентативности. Первая возникает из-за неправильных или неточных сведений по причинам непонимания существа вопроса, невнимательности регистратора при заполнении анкет, формуляров и т.п. Она достаточно легко обнаруживается и устраняется. Вторая возникает из-за несоблюдения принципа случайности отбора единиц в выборку. Ее сложнее обнаружить и устранить, она гораздо больше первой и потому ее измерение является основной задачей выборочного наблюдения.

Для измерения ошибки выборки определяется ее средняя ошибка по формуле (39) для повторного отбора и по формуле (40) – для бесповторного:

Из формул (39) и (40) видно, что средняя ошибка меньше у бесповторной выборки, что и обусловливает ее более широкое применение.

Предельная ошибка выборки

Учитывая, что на основе выборочного обследования нельзя точно оценить обобщающую характеристику ГС, необходимо найти пределы, в которых он находится. В конкретной выборке разность 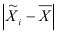может быть больше, меньше или равна 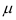. Каждое из отклонений 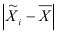от 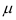имеет определенную вероятность. При выборочном обследовании реальное значение X в ГС неизвестно. Зная среднюю ошибку выборки, с определенной вероятностью можно оценить отклонение выборочной средней от генеральной и установить пределы, в которых находится изучаемый параметр (в данном случае среднее значение) в генеральной совокупности. Отклонение выборочной характеристики от генеральной называется предельной ошибкой выборки . Она определяется в долях средней ошибки с заданной вероятностью, т.е.

где t – коэффициент доверия, зависящий от вероятности, с которой определяется предельная ошибка выборки.

Вероятность появления определенной ошибки выборки находят с помощью теорем теории вероятностей. Согласно теореме Чебышёва, при достаточно большом объеме выборки и ограниченной дисперсии генеральной ГС вероятность того, что разность между выборочной средней и генеральной средней будет сколь угодно мала, близка к единице:

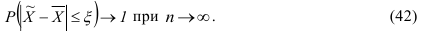
А. М. Ляпунов доказал, что независимо от характера распределения генеральной ГС при увеличении объема выборки распределение вероятностей появления того или иного значения выборочной средней приближается к нормальному распределению (центральная предельная теорема). Следовательно, вероятность отклонения выборочной средней от генеральной средней, т.е. вероятность появления заданной предельной ошибки, также подчиняется указанному закону и может быть найдена как функция от t с помощью интеграла вероятностей Лапласа:

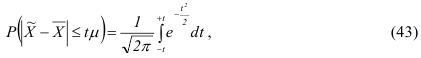
где 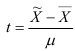– нормированное отклонение выборочной средней от генеральной средней.

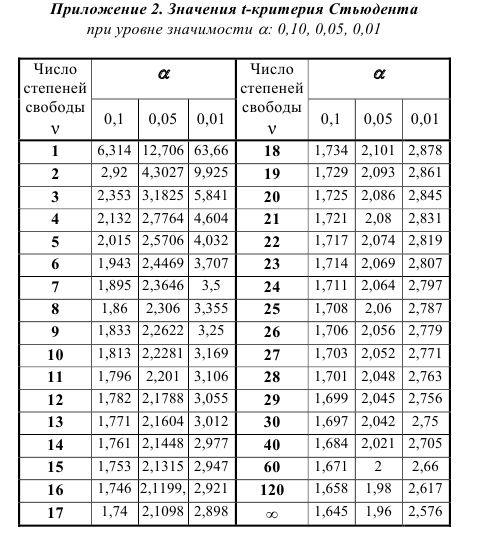
Значения P (интеграла Лапласа) для разных t рассчитаны и имеются в специальной таблице, которая приведена в Приложении 1.

Вероятность, которая принимается при расчете выборочной характеристики, называется доверительной. Чаще всего принимают вероятность P = 0,950, которая означает, что только в 5 случаях из 100 ошибка может выйти за установленные границы. Задавшись конкретным уровнем вероятности, выбирают величину нормированного отклонения t по Приложению 1 и рассчитывают предельную ошибку выборки по формуле (41).

После расчета предельной ошибки находят доверительный интервал обобщающей характеристики ГС совокупности по формуле (44) – для среднего значения, и по формуле (45) – для доли единиц, обладающих каким-либо значением признака:

Следовательно, при выборочном наблюдении определяется не одно, точное значение обобщающей характеристики ГС, а лишь ее доверительный интервал с заданным уровнем вероятности. И это серьезный недостаток выборочного метода статистики.

Необходимая численность выборки

Разрабатывая программу выборочного наблюдения, задаются конкретным значением предельной ошибки и уровнем вероятности. Неизвестной остается минимальная численность выборки, обеспечивающая заданную точность. Ее можно получить из формул средней и предельной ошибок в зависимости от типа выборки. Так, подставляя формулы сначала (39) и затем (40) в формулу (41) и решая ее относительно численности выборки, получим следующие формулы: для повторной выборки 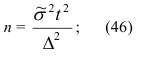для бесповторной выборки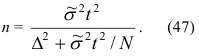

Вариация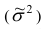значений признака к началу выборочного наблюдения как правило неизвестна, поэтому ее берут приближенно одним из способов:

1) берется из предыдущих выборочных наблюдений;
2) по правилу «трех сигм», согласно которому в размахе вариации укладывается примерно 6 стандартных отклонений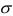
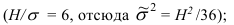
3) если приблизительно известна средняя величина изучаемого признака, то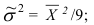
4) если неизвестна дисперсия доли единиц, обладающих каким-либо значением признака, то используется ее максимально возможная величина 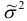= 0,25.

Возможно эта страница вам будет полезна:

Помощь по статистике

Контрольная работа 7.

На предприятии в порядке случайной бесповторной выборки было опрошено 100 рабочих из 1000 и получены следующие данные об их доходе за месяц (таблица 8):

Таблица 8. Результаты бесповторного выборочного наблюдения на предприятии

С вероятностью 0,950 определить:

1) среднемесячный размер дохода работников данного предприятия;
2) долю рабочих предприятия, имеющих месячный доход более 700 у.е.;
3) необходимую численность выборки при определении среднемесячного дохода работников предприятия, чтобы не ошибиться более чем на 50 у.е.;
4) необходимую численность выборки при определении доли рабочих с размером месячного дохода более 700 у.е., чтобы при этом не ошибиться более чем на 5%.

Решение:

Для расчета обобщающих характеристик выборки построим вспомогательную таблицу 9.

Таблица 9. Вспомогательные расчеты для решения задачи

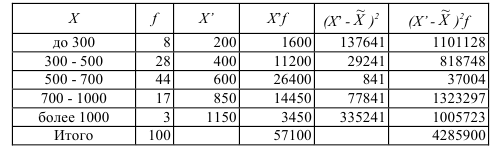
По формуле (11) рассчитаем средний доход в выборке: 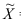= 57100/100 = 571 (у.е.). Применив формулу (28) и рассчитав ее числитель в последнем столбце таблицы, получим дисперсию среднего выборочного дохода: 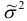= 4285900/100 = 42859.

Теперь можно определить среднюю ошибку выборки по формуле (40):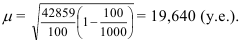 В нашей задаче 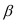= 0,950, значит t = 1,96. Тогда предельная ошибка выборки по формуле (41): = 1,96*19,64 = 38,494 (у.е.).

Для определения средней ошибки выборки при определении доли рабочих с доходами более 700 у.е. в ГС необходимо определить их долю: w = 20/100 = 0,2 или 20%, а затем ее дисперсию по формуле 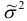= w(1-w) = 0,2*(1–0,2) = 0,16. Тогда можно рассчитать среднюю ошибку выборки по формуле (40): 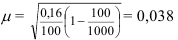или 3,8%. А затем и предельную ошибку выборки по формуле (41): = 1,96*0,038 = 0,075 или 7,5%.

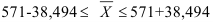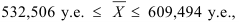Доверительный интервал среднего дохода находим по формуле (44): или то есть средний доход всех рабочих предприятия с вероятностью 95% будет лежать в пределах от 532,5 до 609,5 у.е.

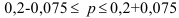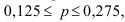Аналогично определяем доверительный интервал для доли по формуле (45): или то есть доля рабочих с доходами более 700 у.е. на всем предприятии с вероятностью 95% будет лежать в пределах от 12,5% до 27,5%.

В нашей задаче выборка бесповторная, значит, воспользуемся формулой (47), в которую подставим уже рассчитанные дисперсии среднего выборочного дохода рабочих (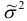 = 42859) и доли рабочих с доходами более 700 у.е. ( 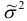= 0,16):

Таким образом, необходимо включить в выборку не менее 62 рабочих при определении среднего месячного дохода работников предприятия, чтобы не ошибиться более чем на 50 у.е., и не менее 197 рабочих при определении доли рабочих с размером месячного дохода более 700 у.е., чтобы при этом не ошибиться более чем на 5%.

Ряды динамики, понятие о рядах динамики

Одной из важнейших задач статистики является изучение изменений анализируемых показателей во времени, то есть их динамика. Эта задача решается при помощи анализа рядов динамики (временных рядов).

Ряд динамики – это числовые значения определенного статистического показателя в последовательные моменты или периоды времени (т.е. расположенные в хронологическом порядке).

Числовые значения того или иного статистического показателя, составляющего ряд динамики, называют уровнями ряда и обычно обозначают через y. Первый член ряда 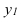называют начальным (базисным) уровнем, а последний 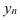– конечным. Моменты или периоды времени, к которым относятся уровни, обозначают через t.

Ряды динамики, как правило, представляют в виде таблицы (см. табл. 10) или графически (см. рис. 5), причем по оси абсцисс строится шкала времени t, а по оси ординат – шкала уровней ряда y.

Таблица 10. Внешнеторговый оборот (ВО) России за период 2000-2006 гг.

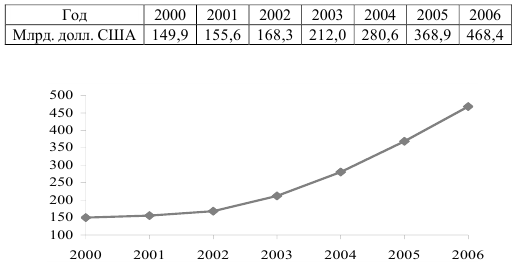
Рис. 5. Внешнеторговый оборот (ВО) России за период 2000-2006 гг.

Данные табл. 10 и рис. 5 наглядно иллюстрируют ежегодный рост внешнеторгового оборота (ВО) в России за период 2000-2006 гг.

Показатели изменения уровней ряда динамики

Анализ рядов динамики начинается с определения того, как именно изменяются уровни ряда (увеличиваются, уменьшаются или остаются неизменными) в абсолютном и относительном выражении. Чтобы проследить за направлением и размером изменений уровней во времени, для рядов динамики рассчитывают показатели изменения уровней ряда динамики:

– абсолютное изменение (абсолютный прирост);
– относительное изменение (темп роста или индекс динамики);
– темп изменения (темп прироста).

Все эти показатели могут определяться базисным способом, когда уровень данного периода сравнивается с первым (базисным) периодом, либо цепным способом – когда сравниваются два уровня соседних периодов.

Абсолютное изменение (абсолютный прирост) уровней рассчитывается как разность между двумя уровнями ряда по формуле (48) – для базисного способа сравнения или по формуле (49) – для цепного. Оно показывает, на сколько (в единицах показателей ряда) уровень одного (i-того) периода больше или меньше уровня какого-либо предшествующего периода, и, следовательно, может иметь знак «+» (при увеличении уровней) или «–» (при уменьшении уровней).

В табл. 11 в столбце 3 рассчитаны базисные абсолютные изменения по формуле (48), а в столбце 4 – цепные абсолютные изменения по формуле (49).

Таблица 11. Анализ динамики ВО России

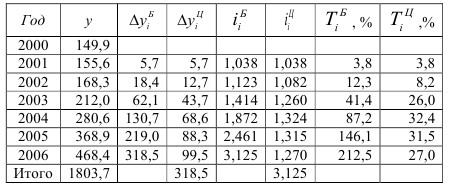
Между базисными и цепными абсолютными изменениями существует взаимосвязь: сумма цепных абсолютных изменений равна последнему базисному изменению, то есть

В нашем примере про ВО подтверждается правильность расчета абсолютных изменений по формуле (50): 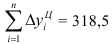рассчитана в итоговой строке 4-го столбца, а 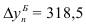– в предпоследней строке 3-го столбца табл. 11.

Относительное изменение (темп роста или индекс динамики) уровней рассчитывается как отношение (деление) двух уровней ряда по формуле (51) – для базисного способа сравнения или по формуле (52) – для цепного.

Относительное изменение показывает во сколько раз уровень данного периода больше уровня какоголибо предшествующего периода (при 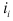>1) или какую его часть составляет (при 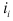<1). Относительное изменение может выражаться в виде коэффициентов, то есть простого кратного отношения (если база сравнения принимается за единицу), и в процентах (если база сравнения принимается за 100 единиц) путем домножения относительного изменения на 100%.

В табл. 11 в столбце 5 рассчитаны базисные относительные изменения по формуле (51), а в столбце 6 – цепные относительные изменения по формуле (52).

Между базисными и цепными относительными изменениями существует взаимосвязь: произведение цепных относительных изменений равно последнему базисному изменению, то есть

В нашем примере про ВО подтверждается правильность расчета относительных изменений по формуле (53):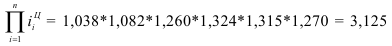рассчитано по данным 6-го столбца, а 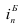= 3,125 – в предпоследней строке 5-го столбца табл. 11.

Темп изменения (темп прироста) уровней – относительный показатель, показывающий, на сколько процентов данный уровень больше (или меньше) другого, принимаемого за базу сравнения. Он рассчитывается путем вычитания из относительного изменения 100%, то есть по формуле (54):

или как процентное отношение абсолютного изменения к тому уровню, по сравнению с которым рассчитано абсолютное изменение (базисный уровень), то есть по формуле (55):

В табл. 11 в столбце 7 рассчитаны базисные темпы изменения ВО по формуле (54), а в столбце 8 – цепные темпы изменения по формуле (55). Все расчеты в табл. 11 свидетельствуют о ежегодном росте ВО России за период 2000-2006 гг.

Средние показатели ряда динамики

Каждый ряд динамики можно рассматривать как некую совокупность n меняющихся во времени показателей, которые можно обобщить в виде средних величин. Такие обобщенные (средние) показатели особенно необходимы при сравнении динамики изменений того или иного показателя ВЭД в разные периоды, в разных странах и т.д.

Обобщенной характеристикой ряда динамики служит прежде всего средний уровень ряда 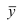. Для разных видов рядов динамики он рассчитывается неодинаково. Ряды динамики бывают равномерные (с равными интервалами времени между уровнями), для которых средний уровень определяется по простой формуле средней величины, и неравномерные (с неравными интервалами), для которых используются формулы средних взвешенных (по интервалам времени) величин. В интервальном ряду динамики (в котором время задано в виде промежутков времени, к которым относятся уровни) 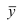определяется по формуле средней арифметической, а в моментном ряду (в котором время задано в виде конкретных моментов времени или дат, к которым относятся уровни) – по формуле средней хронологической. В табл. 12 приводятся виды рядов динамики и соответствующие формулы для расчета их среднего уровня .

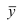Таблица 12. Виды средних величин, применяемых при расчете среднего уровня

В нашем примере про ВО России за период 2000-2006 гг. имеем равномерный интервальный ряд динамики, поэтому его средний уровень определяем по формуле (56): 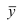= 1803,7/7 = 257,671, то есть ВО России в период 2000-2006 гг. составлял ежегодно в среднем 257,671 млрд. долл. США.

Кроме среднего уровня ряда рассчитываются и другие средние показатели:

– среднее абсолютное изменение (средний абсолютный прирост);
– среднее относительное изменение (средний темп роста);
– средний темп изменения (средний темп прироста).

Каждый из этих показателей может рассчитываться базисным и цепным способом.

Базисное среднее абсолютное изменение – это частное от деления последнего базисного абсолютного изменения на количество изменений уровней (60); цепное среднее абсолютное изменение уровней ряда – это частное от деления суммы всех цепных абсолютных изменений на количество изменений (61):

По знаку средних абсолютных изменений также судят о характере изменения явления в среднем: рост, спад или стабильность. Очевидно, что числители формулы (60) и (61) равны между собой по формуле (50), значит, среднее абсолютное изменение не зависит от способа расчета (базисный или цепной), так как результат получится одинаковый. В нашей задаче по формуле (60) или (61): 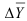= 318,5/6 = 53,083, то есть ежегодно в среднем ВО растет на 53,083 млрд. долл.

Наряду со средним абсолютным изменением рассчитывается и среднее относительное. Базисное среднее относительное изменение определяется по формуле (62), а цепное среднее относительное изменение – по формуле (63):

Естественно, базисное и цепное среднее относительное изменения должны быть одинаковыми и сравнением их с критериальным значением 1 делается вывод о характере изменения явления в среднем: рост, спад или стабильность. В нашем примере про ВО: 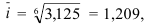то есть ежегодно в среднем в период 2000-2006 гг. ВО России растет в 1,209 раза.

Вычитанием 100% из среднего относительного изменения образуется соответствующий средний темп изменения, по знаку которого также можно судить о характере изменения изучаемого явления, отраженного данным рядом динамики. В нашем примере про ВО: 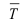= 1,209 – 1 = 0,209, то есть ежегодно в среднем в период 2000-2006 гг. ВО России растет на 20,9%.

Методы выявления основной тенденции (тренда) в рядах динамики

Одна из основных задач изучения рядов динамики – выявить основную тенденцию (закономерность) в изменении уровней ряда, именуемую трендом. Закономерность в изменении уровней ряда в одних случаях проявляется наглядно, в других – может маскироваться колебаниями случайного или неслучайного характера. Поэтому, чтобы сделать правильные выводы о закономерностях развития того или иного показателя, надо суметь отделить тренд от колебаний, вызванных случайными кратковременными причинами. На основании выделенного тренда можно экстраполировать (прогнозировать) развитие явления в будущем. С этой целью (устранить колебания, вызванные случайными причинами) ряды динамики подвергают обработке.

Существует несколько методов обработки рядов динамики, помогающих выявить основную тенденцию изменения уровней ряда, а именно: метод укрупнения интервалов, метод скользящей средней и аналитическое выравнивание. Во всех методах вместо фактических уровней при обработке ряда рассчитываются иные (расчетные) уровни, в которых тем или иным способом взаимопогашается действие случайных факторов и тем самым уменьшается колеблемость уровней. Последние в результате становятся как бы «выравненными», «сглаженными» по отношению к исходным фактическим данным. Такие методы обработки рядов динамики называются сглаживанием или выравниванием рядов динамики.

Простейший метод сглаживания уровней ряда – укрупнения интервалов, для определяется итоговое значение или средняя величина исследуемого показателя. Этот метод особенно эффективен, если первоначальные уровни ряда относятся к коротким промежуткам времени. Например, если имеются данные о ежесуточном производстве мороженого на предприятии за месяц, то, естественно, в таком ряду возможны значительные колебания уровней, так как чем меньше период, за который приводятся данные, тем больше влияние случайных факторов. Чтобы устранить это влияние, рекомендуется укрупнить интервалы времени, например до 5 или 10 дней, и для этих укрупненных интервалов рассчитать общий или среднесуточный объем производства (соответственно по пятидневкам или декадам). В ряду с укрупненными интервалами времени закономерность изменения уровней будет более наглядной.

По своей сути метод скользящей средней похож на метод укрупнения интервалов, но в данном случае фактические уровни заменяются средними уровнями, рассчитанными для последовательно подвижных (скользящих) укрупненных интервалов, охватывающих m уровней ряда. Например, если принять m=3, то сначала рассчитывается средняя величина из первых трех уровней, затем находится средняя величина из 2-го, 3-го и 4-го уровней, потом из 3-го, 4-го и 5-го и т.д., т.е. каждый раз в сумме трех уровней появляется новый уровень, а два остаются прежними, что и обусловливает взаимопогашение случайных колебаний в средних уровнях. Рассчитанные из m членов скользящие средние относятся к середине (центру) каждого рассматриваемого интервала.

Сглаживание методом скользящей средней можно проводить по любому числу членов m, но удобнее, если m – нечетное число, так как в этом случае скользящая средняя сразу относится к конкретной временнОй точке – середине (центру) интервала. Если же m – четное, то скользящая средняя относится к промежутку между временнЫми точками: например, при сглаживании по четырем членам (m=4) средняя из первых четырех уровней будет находиться между второй и третьей временной точкой, следующая – между третьей и четвертой и т.д. Тогда, чтобы сглаженные уровни относились непосредственно к конкретным временнЫм точкам, из каждой пары смежных промежуточных значений скользящих средних находят среднюю арифметическую, которую относят к временной точке, находящейся между смежными. Такой прием двойного расчета сглаженных уровней называется центрированием.

Недостатком метода скользящей средней является то, что сглаженный ряд укорачивается по сравнению с фактическим с двух концов: при нечетном m на (m-1)/2, а при четном m – на m/2 с каждого конца. Применяя этот метод, надо помнить, что он сглаживает (устраняет) лишь случайные колебания. Если же, например, ряд содержит сезонную волну (см. 6.6), она сохранится и после сглаживания методом скользящей средней. Кроме того, этот метод сглаживания, как и метод укрупнения интервалов не позволяет выражать общую тенденцию изменения уровней в виде математической модели.

Наиболее совершенным методом обработки рядов динамики в целях устранения случайных колебаний и выявления тренда является выравнивание уровней ряда по аналитическим формулам (или аналитическое выравнивание). Суть аналитического выравнивания заключается в замене эмпирических (фактических, исходных) уровней 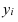теоретическими 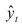, которые рассчитаны по определенному уравнению, принятому за математическую модель тренда, где теоретические уровни рассматриваются как функция времени: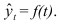

При этом каждый фактический уровень 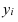рассматривается обычно как сумма двух составляющих:

где 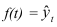— систематическая составляющая, отражающая тренд и выраженная определенным уравнением; 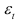— случайная величина, вызывающая колебания уровней вокруг тренда.

Задача аналитического выравнивания сводится к следующему:

1) определение на основе фактических данных формы (вида) гипотетической функции 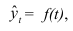способной наиболее адекватно отразить тенденцию развития исследуемого показателя;
2) нахождение по эмпирическим данным параметров указанной функции (уравнения);
3) расчет по найденному уравнению теоретических (выравненных) уровней. В аналитическом выравнивании наиболее часто используются простейшие функции, представленные в табл. 13, где обозначено 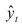— теоретические (выравненные) уровни (читается как «игрек, выравненный по t»); t – условное обозначение времени (1, 2, 3 …);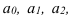… – параметры аналитической функции; k – число гармоник (при выравнивании по ряду Фурье). Выбор той или иной функции для выравнивания ряда динамики осуществляется на основании графического изображения эмпирических данных. Если по тем или иным причинам уровни эмпирического ряда трудно описать одной функцией, следует разбить анализируемый период на отдельные части и затем выровнять каждую часть по соответствующей кривой.

Таблица 13. Виды математических функций, используемые при выравнивании

Нередко один и тот же ряд можно выровнять по разным аналитическим функциям и получить довольно близкие результаты. В нашем примере про ВО России можно произвести выравнивание и по прямой линии, и по параболе. Чтобы решить вопрос о том, использование какой кривой дает лучший результат, обычно сопоставляют суммы квадратов отклонений эмпирических уровней от теоретических (остатки), рассчитанным по разным функциям, то есть:

Та функция, при которой эта сумма минимальна, считается наиболее адекватной, приемлемой. Однако сравнивать непосредственно суммы квадратов отклонений можно в том случае, если сравниваемые уравнения имеют одинаковое число параметров. Если же число параметров k разное, то каждую сумму квадратов делят на разность (n – k), выступающую в роли числа степеней свободы, и сравнивают уже квадраты отклонений уровней, рассчитанные на одну степень свободы (т.е. остаточные дисперсии на одну степень свободы).

Параметры искомых уравнений (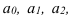…) при аналитическом выравнивании могут быть определены по-разному, но наиболее распространенным методом является метод наименьших квадратов (МНК). При этом методе учитываются все эмпирические уровни и должна обеспечиваться минимальная сумма квадратов отклонений эмпирических значений уровней y от теоретических уровней

В частности, при выравнивании по прямой вида (65) параметры 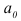и 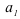отыскиваются по МНК следующим образом. В формуле (73) вместо 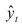записываем его конкретное выражение 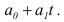Тогда 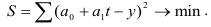Дальнейшее решение сводится к задаче на экстремум, т.е. к определению того, при каком значени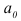и и 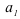функция двух переменных S может достигнуть минимума. Как известно, для этого надо найти частные производные S по 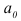и 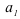, приравнять их к нулю и после элементарных преобразований решить систему двух уравнений с двумя неизвестными. В соответствии с вышеизложенным найдем частные производные:

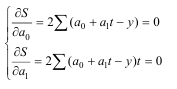
Сократив каждое уравнение на 2, раскрыв скобки и перенеся члены с y в правую сторону, а остальные – оставив в левой, получим систему нормальных уравнений:

где n – количество уровней ряда; t – порядковый номер в условном обозначении периода или момента времени; y – уровни эмпирического ряда. Эта система и, соответственно, расчет параметров 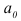и 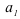упрощаются, если отсчет времени ведется от середины ряда(*при расчете параметров уравнения тренда на ЭВМ необходимость вести отсчет от середины ряда динамики отпадает. Например, для получения уравнения тренда в Microsoft Office Excel необходимо построить его график с помощью «Мастера диаграмм», после чего вызвать контекстное меню, нажав на правую кнопку мыши на построенном графике, и выбрать пункт «Добавить линию тренда», в появившемся окне выбрать подходящую математическую функцию и установить галочку «показывать уравнение на диаграмме»). Например, при нечетном числе уровней (как в нашем примере про ВО России – 7 уровней) серединная точка времени (год, месяц) принимается за нуль, тогда предшествующие периоды обозначаются соответственно –1, –2, –3 и т.д., а следующие за средним (центральным) – соответственно 1, 2, 3 и т.д. (см. 3-й столбец табл. 14). 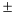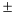При четном числе уровней два серединных момента (периода) времени обозначают –1 и +1, а все последующие и предыдущие, соответственно, через два интервала: 3, 5 , 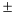7 и т.д.

При таком порядке отсчета времени (от середины ряда) 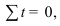поэтому, система нормальных уравнений (74) упрощается до следующих двух уравнений, каждое из которых решается самостоятельно:

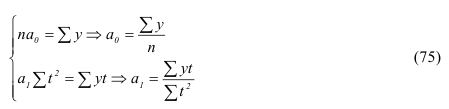
Как видим, при такой нумерации периодов параметр 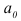представляет собой средний уровень равномерного интервального ряда, то есть формулу (56). Определим по формуле (75) параметры уравнения прямой для нашего примера про ВО России, для чего исходные данные и все расчеты необходимых сумм представим в табл. 14.

Таблица 14. Вспомогательные расчеты для линейного тренда

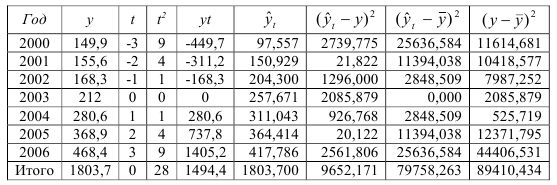
Из табл. 14 получаем, что: 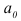= 1803,7/7 = 257,671 и 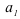= 1494,4/28 = 53,371. Отсюда искомое уравнение тренда: 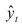=257,671+53,371t. В 6-м столбце табл. 14 приведены теоретические (трендовые) уровни, рассчитанные по этому уравнению, а в итоге 7-го столбца – остатки по формуле (72). Для иллюстрации построим график эмпирических и трендовых уровней – рис. 6.

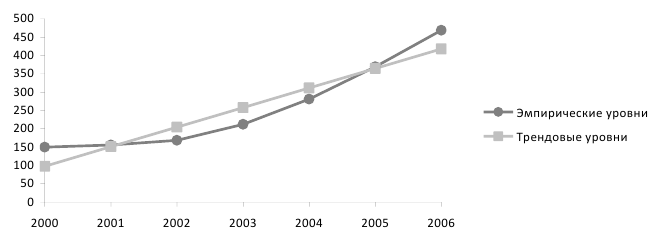
Рис. 6. Эмпирические и трендовые уровни ряда динамики ВО России

Возможно эта страница вам будет полезна:

Заказать работу по статистике

Оценка адекватности тренда и прогнозирование

Для найденного уравнения тренда необходимо провести оценку его надежности (адекватности), что осуществляется обычно с помощью критерия Фишера, сравнивая его расчетное значение 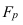с теоретическим (табличным) значением 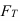(Приложение 3). При этом расчетный критерий Фишера определяется по формуле (76):

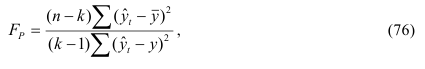
где k – число параметров (членов) выбранного уравнения тренда.

Для проверки правильности расчета сумм в формуле (76) можно использовать следующее равенство (77):

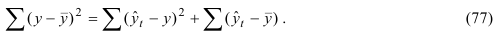
В нашем примере про ВО равенство (77) соблюдается (необходимые суммы рассчитаны в трех последних столбцах табл. 14): 89410,434 = 9652,171 + 79758,263.

Сравнение расчетного и теоретического значений критерия Фишера ведется при заданном уровне значимости (вероятности сделать неверный прогноз) с учетом степеней свободы: 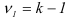и 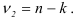При условии 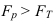считается, что выбранная математическая модель ряда динамики адекватно отражает обнаруженный в нем тренд. Проверим тренд на адекватность в нашем примере про ВО по формуле (76): 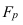= 79758,263*5/(9652,171*1) = 41,32 > 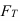, значит, модель адекватна и ее можно использовать для прогнозирования (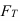= 6,61 находим по Приложению 3 в 1-ом столбце 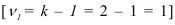и 5-й строке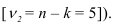

Как уже было отмечено ранее, в нашем примере про ВО России можно произвести выравнивание не только по прямой линии, но и по параболе, чего делать не будем, так как уже найденный линейный тренд адекватно описывает тенденцию.

При составлении прогнозов уровней социально-экономических явлений обычно оперируют не точечной, а интервальной оценкой, рассчитывая так называемые доверительные интервалы прогноза. Границы интервалов определяются по формуле (78):

где 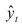– точечный прогноз, рассчитанный по модели тренда; 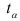– коэффициент доверия по распределению Стьюдента при уровне значимости 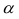и числе степеней свободы 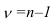(Приложение 2)(*используется при малом количестве уровней (n<30), в противном случае (n>30) вместо 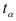используют коэффициент доверия t нормального закона распределения (Приложение 1)); 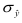– ошибка аппроксимации, определяемая по формуле (79):

Спрогнозируем ВО России на 2007 и 2008 годы с вероятностью 0,95 (значимостью 0,05), для чего найдем ошибку аппроксимации по формуле (79): 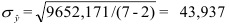и найдем коэффициент доверия по распределению Стьюдента по Приложению 2: 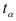= 2,4469 при 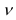= 7 – 1= 6. Прогноз на 2007 и 2008 годы с вероятностью 0,95 по формуле (78):

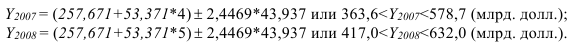
Как видно из полученных прогнозов, доверительный интервал достаточно широк (из-за достаточно большой величины ошибки аппроксимации). Более точный прогноз можно получить при выравнивании по параболе 2-го порядка.

Статистическое изучение взаимосвязей, понятие корреляционной зависимости

Один из наиболее общих законов объективного мира – закон всеобщей связи и зависимости между явлениями. Естественно, что, исследуя явления в самых различных областях, статистика неизбежно сталкивается с зависимостями как между количественными, так и между качественными показателями, признаками. Ее задача – обнаружить (выявить) такие зависимости и дать им количественную характеристику.

Среди взаимосвязанных признаков (показателей) одни могут рассматриваться как определенные факторы, влияющие на изменение других (факторные), а вторые (результативные) – как следствие, результат влияния первых.

Существует 2 вида связи между отдельными признаками: функциональная и стохастическая (статистическая), частным случаем которой является корреляционная.

Связь между двумя переменными x и y называется функциональной, если определенному значению переменной x строго соответствует одно или несколько значений другой переменной y, и с изменением значения x значение y меняется строго определенно. Такие связи обычно встречаются в точных науках. Например, известно, что площадь квадрата равна квадрату его стороны 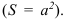Это соотношение характерно для каждого единичного случая (квадрата), это так называемая жестко детерминированная связь. Такие связи можно встретить и в области экономических явлений. Например, при простой сдельной оплате труда связь между оплатой труда y и количеством изготовленных изделий x при фиксированной расценке за одну деталь, например 5 руб., легко выразить формулой y = 5x .. Для изучения функциональных связей применяется индексный метод, который рассматривается в теме 7.

Существуют и иного рода связи, где взаимно действуют многие факторы, комбинация которых приводит к вариации значений результативного признака (показателя) при одинаковом значении факторного признака. Например, при изучении зависимости величины таможенных платежей, поступающих в федеральный бюджет, от количества товаров, перемещаемых через таможенную границу государства, (или от стоимостного товарооборота) последние будут рассматриваться как факторный признак, а величина таможенных платежей – как результативный. Между ними нет жестко детерминированной связи, т.е. при одном и том же количестве перемещенных через таможенную границу товаров (или стоимости товарооборота) величина таможенных платежей, перечисленных разными таможнями будет различной, так как кроме количества товаров, перемещаемых через таможенную границу государства, (или стоимость товарооборота) на величину таможенных платежей влияет много других факторов (различная номенклатура товаров, для которых применяются различные таможенные пошлины, сборы и льготы; различные таможенные режимы перемещения товаров через таможенную границу и др.), комбинация которых вызывает вариацию величины таможенных платежей.

Там, где взаимодействует множество факторов, в том числе и случайных, выявить зависимости, рассматривая единичный случай, невозможно. Такие связи можно обнаружить только при массовом наблюдении как статистические закономерности (*проявление стохастических связей подвержено действию закона больших чисел: лишь в достаточно большом числе единиц индивидуальные особенности сгладятся, случайности взаимопогасятся и зависимость, если она имеет существенную силу, проявится достаточно отчетливо). Выявленная таким образом связь именуется стохастической (*термин «стохастический» происходит от греч. «stochos» – мишень. Стреляя в мишень, даже хороший стрелок редко попадает в ее центр, выстрелы ложатся в некоторой близости от него. Другими словами стохастическая связь означает приблизительный характер значений признака).

Корреляционная связь (*термин «корреляция» ввел в статистику английский биолог и статистик Ф. Гальтон в конце XIX в., под которым понималась «как бы связь», т.е. связь в форме, отличающейся от функциональной. Еще ранее этот термин применил француз Ж.Кювье в палеонтологии, где под законом корреляции частей животных он понимал возможность восстановить по найденным в раскопках частям облик всего животного) – понятие более узкое, чем стохастическая связь, это ее частный случай. Именно корреляционные связи являются предметом изучения статистики.

Корреляционная связь – это связь, проявляющаяся при большом числе наблюдений в виде определенной зависимости между средним значением результативного признака и признакамифакторами. Другими словами, корреляционную связь условно можно рассматривать как своего рода функциональную связь средней величины одного признака (результативного) со значением другого (или других). При этом, если рассматривается связь средней величины результативного показателя y с одним признаком-фактором x, корреляция называется парной, а если факторных признаков 2 и более 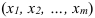– множественной (*множественная корреляция изучается в курсе эконометрики на основе применения компьютерных программ (напр., специальная надстройка к Excel, SPSS и др.), в курсе статистики изучается только парная корреляция).

По характеру изменений x и y в парной корреляции различают прямую и обратную связь. При прямой связи значения обоих признаков изменяются в одном направлении, т.е. с увеличением (уменьшением) значений x увеличиваются (уменьшаются) и значения y. При обратной связи значения факторного и результативного признаков изменяются в разных направлениях.

Изучение корреляционных связей сводится в основном к решению следующих задач:

1) выявление наличия (отсутствия) корреляционной связи между изучаемыми признаками;
2) измерение тесноты связи между двумя (и более) признаками с помощью специальных коэффициентов (эта часть исследования именуется корреляционным анализом);
3) определение уравнения регрессии – математической модели, в которой среднее значение результативного признака у рассматривается как функция одной или нескольких переменных – факторных признаков (эта часть исследования именуется регрессионным анализом).

Общий термин «корреляционно-регрессионный анализ» подразумевает всестороннее исследование корреляционных связей (т.е. решение всех трех задач).

Корреляционно-регрессионный анализ находит широкое применение в статистике. Рассмотрим его практическое применение на примере данных таможенной статистики внешней торговли России в 2006 году – таблица 15.

Таблица 15. Величина внешнеторгового оборота и таможенных платежей

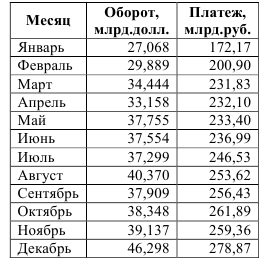
В качестве факторного признака x примем стоимостной внешнеторговый товарооборот в млрд. долл. США, а в качестве результативного признака y – величину таможенных платежей в федеральный бюджет в млрд. руб.

Методы выявления и оценки корреляционной связи

Для выявления наличия и характера корреляционной связи между двумя признаками в статистике используется ряд методов.

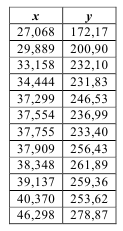
1. Рассмотрение параллельных данных (значений x и y в каждой из n единиц). Единицы наблюдения необходимо расположить по возрастанию значений факторного признака х (как в таблице справа) и затем сравнить с ним (визуально) поведение результативного признака у.
В нашей задаче в 6 случаях по мере увеличения значений x увеличиваются и значения y, а в 5 случаях этого не происходит, поэтому затруднительно говорить о прямой связи между х и у.

2. Графический метод – это графическое изображение корреляционной зависимости. Для этого, имея n взаимосвязанных пар значений x и y и пользуясь прямоугольной системой координат, каждую такую пару изображают в виде точки на плоскости с координатами x и y. Совокупность полученных точек представляет собой корреляционное поле (рис. 7), а соединяя последовательно нанесенные точки отрезками, получают ломаную линию, именуемую эмпирической линией регрессии (рис. 8)

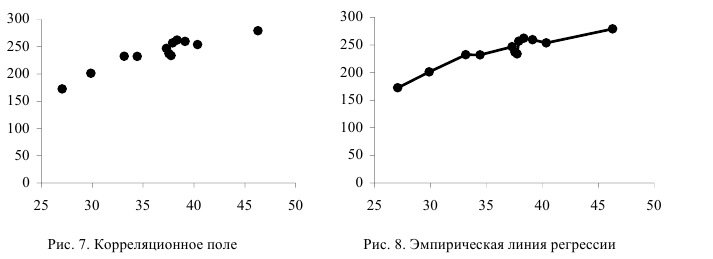
Визуально анализируя график, можно предположить характер зависимости между признаками x и y. В нашей задаче эмпирическая линия регрессии (рис.8) похожа на восходящую прямую, что позволяет выдвинуть гипотезу о наличии прямой зависимости между величиной стоимостного внешнеторгового товарооборота и величиной таможенных платежей в федеральный бюджет.

3. Коэффициент корреляции знаков (Фехнера) – простейший показатель тесноты связи, основанный на сравнении поведения отклонений индивидуальных значений каждого признака (x и y) от своей средней величины. При этом во внимание принимаются не величины отклонени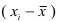й и 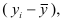а их знаки («+» или «–»). Определив знаки отклонений от средней величины в каждом ряду, рассматривают все пары знаков и подсчитывают число их совпадений (С) и несовпадений (Н). Тогда коэффициент Фехнера рассчитывается как отношение разности чисел пар совпадений и несовпадений знаков к их сумме, т.е. к общему числу наблюдаемых единиц:

Очевидно, что если знаки всех отклонений по каждому признаку совпадут, то 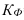=1, что характеризует наличие прямой связи. Если все знаки не совпадут, то 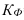=–1 (обратная связь). Если же 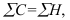то 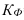=0. Итак, как и любой показатель тесноты связи, коэффициент Фехнера может принимать значения от 0 до 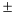1. Однако, если 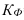=1, то это ни в коей мере нельзя воспринимать как свидетельство функциональной зависимости между х и у. Средние значения факторного и результативного признаков определяем по формуле средней арифметической простой (10):

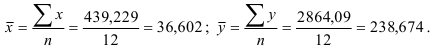
В двух последних столбцах таблицы 16 приведены знаки отклонений каждого х и у от своей средней величины. Число совпадений знаков – 10, а несовпадений – 2, тогда определяем коэффициент корреляции знаков (Фехнера) по формуле (80):

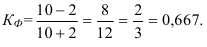
Таблица 16. Вспомогательная таблица для расчета коэффициента Фехнера

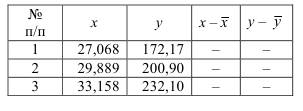
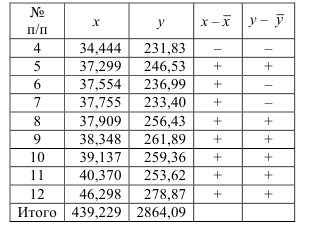
Обычно такое значение показателя тесноты связи характеризует заметную прямую зависимость между x и y, однако, следует иметь в виду, что поскольку КФ зависит только от знаков и не учитывает величину самих отклонений х и у от их средних величин, то он практически характеризует не столько тесноту связи, сколько ее наличие и направление.

4. Линейный коэффициент корреляции – самый популярный измеритель тесноты линейной связи между двумя количественными признаками x и y. Он основан на предположении, что при полной независимости признаков (*данное условие означает отстутствие автокорреляции в коррелируемых рядах динамики) x и у отклонения значений факторного признака от средней 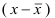носят случайный характер и должны случайно сочетаться с различными отклонениями 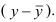При наличии значительного перевеса совпадений или несовпадений таких отклонений делается предположение о наличии связи между x и y.

В отличие от 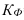в линейном коэффициенте корреляции учитываются не только знаки отклонений от средних величин, но и значения самих отклонений, выраженные для сопоставимости в единицах среднего квадратического отклонения t:

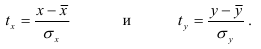
Линейный коэффициент корреляции r представляет собой среднюю величину из произведений нормированных отклонений для x и у:

Числитель формулы (82), деленный на n, представляющий собой среднее произведение отклонений значений двух признаков от их средних значений, называется коэффициентом ковариации – это мера совместной вариации факторного x и результативного y признаков:

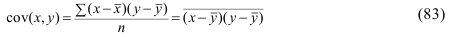
Недостатком коэффициента ковариации является то, что он не нормирован, в отличие от линейного коэффициента корреляции. Очевидно, что линейный коэффициент корреляции представляет собой частное от деления ковариации между x и у на произведение их средних квадратических отклонений:

Путем несложных математических преобразований можно получить и другие модификации формулы линейного коэффициента корреляции, например:

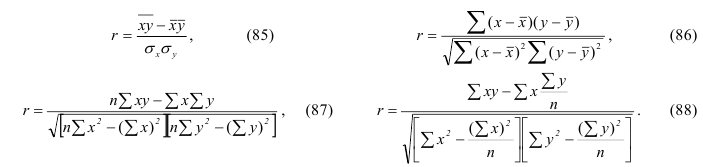
Линейный коэффициент корреляции может принимать значения от –1 до +1, причем знак определяется в ходе решения. Например, если 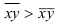, то r по формуле (85) будет положительным, что характеризует прямую зависимость между х и у, в противном случае (r<0) – обратную связь. Если 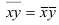, то r=0, что означает отсутствие линейной зависимости между х и у, а при r=1 – функциональная зависимость между х и у . Следовательно, всякое промежуточное значение r от 0 до 1 характеризует степень приближения корреляционной связи между х и у к функциональной. Существует эмпирическое правило (шкала Чэддока) для оценки тесноты связи, представленное в таблице 17.

Таблица 17. Шкала Чэддока

Таким образом, коэффициент корреляции при линейной зависимости служит как мерой тесноты связи, так и показателем, характеризующим степень приближения корреляционной зависимости между х и у к линейной. Поэтому близость значения r к 0 в одних случаях может означать отсутствие связи между х и у , а в других свидетельствовать о том, что зависимость не линейная.

В нашей задаче для расчета r построим вспомогательную таблицу 18.

Таблица 18. Вспомогательные расчеты линейного коэффициента корреляции

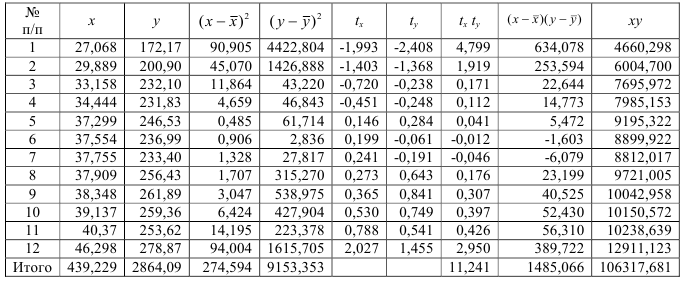
В нашей задаче: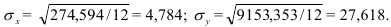
Тогда линейный коэффициент корреляции по формуле (81): r = 11,241/12 = 0,937.
Аналогичный результат получаем по формуле (82): r = 1485,066/(12*4,784*27,618) = 0,937
Или по формуле (85): r = (106317,681/12 – 36,602*238,674) / (4,784*27,618) = 0,937,

Найденное значение свидетельствует о том, что связь между величиной стоимостного внешнеторгового товарооборота и величиной таможенных платежей в федеральный бюджет очень близка к функциональной (сильная по шкале Чэддока). стр.34

Проверка коэффициента корреляции на значимость (существенность). Интерпретируя значение коэффициента корреляции, следует иметь в виду, что он рассчитан для ограниченного числа наблюдений и подвержен случайным колебаниям, как и сами значения x и y, на основе которых он рассчитан.

Другими словами, как любой выборочный показатель, он содержит случайную ошибку и не всегда однозначно отражает действительно реальную связь между изучаемыми показателями.

Для того, чтобы оценить существенность (значимость) самого r и, соответственно, реальность измеряемой связи между x и y, , необходимо рассчитать среднюю квадратическую ошибку коэффициента корреляции 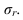Оценка существенности (значимости) r основана на сопоставлении значения r с его средней квадратической ошибкой: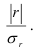

Существуют некоторые особенности расчета σr в зависимости от числа наблюдений (объема выборки) – n.

1. Если число наблюдений достаточно велико (n>30), то 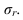рассчитывается по формуле (89):

Обычно, если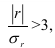 то r считается значимым (существенным), а связь – реальной. Задавшись определенной вероятностью, можно определить доверительные пределы (границы) 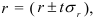где t – коэффициент доверия, рассчитываемый по интегралу Лапласа (см. Приложение 1).

2. Если число наблюдений небольшое (n<30), то 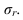рассчитывается по формуле (90):

а значимость r проверяется на основе t-критерия Стьюдента, для чего определяется расчетное значение критерия по формуле (91) и сопоставляется c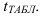

Табличное значение 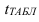находится по таблице распределения t-критерия Стьюдента (см. Приложение 2) при уровне значимости α=1-β и числе степеней свободы ν=n–2. Если 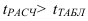, то r считается значимым, а связь между х и у – реальной. В противном случае 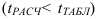считается, что связь между х и у отсутствует, и значение r, отличное от нуля, получено случайно.

В нашей задаче число наблюдений небольшое, значит, оценивать существенность (значимость) линейного коэффициента корреляции будем по формулам (90) и (91):

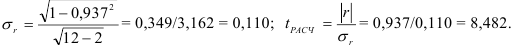
Из приложения 2 видно, что при числе степеней свободы ν = 12 – 2 = 10 (в 10-й строке) и вероятности β = 95% (уровень значимости α =1 – β = 0,05) tтабл=2,2281, а при вероятности 99% (α=0,01) 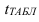=3,169, значит, 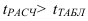, что дает возможность считать линейный коэффициент корреляции r = 0,937 значимым.

5. Подбор уравнения регрессии (*термин «регрессия» ввел в статистику Ф. Гальтон, который изучив большое число семей, установил, что в группе семей высокорослыми отцами сыновья в среднем ниже ростом, чем их отцы, а в группе семей с низкорослыми отцами сыновья в среднем выше отцов, т.е. отклонение роста от среднего в следующем поколении уменьшается – регрессирует) представляет собой математическое описание изменения взаимно коррелируемых величин по эмпирическим (фактическим) данным. Уравнение регрессии должно определить, каким будет среднее значение результативного признака у при том или ином значении факторного признака х, если остальные факторы, влияющие на у и не связанные с х, не учитывать, т.е. абстрагироваться от них. Другими словами, уравнение регрессии можно рассматривать как вероятностную гипотетическую функциональную связь величины результативного признака у со значениями факторного признака х.

Уравнение регрессии можно также назвать теоретической линией регрессии. Рассчитанные по уравнению регрессии значения результативного признака называются теоретическими. Они обычно обозначаются 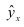или 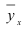(читается: «игрек, выравненный по х») и рассматриваются как функция от х, т.е.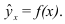

Найти в каждом конкретном случае тип функции, с помощью которой можно наиболее адекватно отразить ту или иную зависимость между признаками х и у, — одна из основных задач регрессионного анализа. Выбор теоретической линии регрессии часто обусловлен формой эмпирической линии регрессии; теоретическая линия как бы сглаживает изломы эмпирической линии регрессии. Кроме того, необходимо учитывать природу изучаемых показателей и специфику их взаимосвязей.

Для аналитической связи между х и у могут использоваться виды уравнений, приведенные в таблице 13 (при условии замены t на x). Обычно зависимость, выражаемую уравнением прямой, называют линейной (или прямолинейной), а все остальные — криволинейными зависимостями. Выбрав тип функции (таблица 13), по эмпирическим данным определяют параметры уравнения. При этом отыскиваемые параметры должны быть такими, при которых рассчитанные по уравнению теоретические значения результативного признака 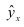были бы максимально близки к эмпирическим данным.

Существует несколько методов нахождения параметров уравнения регрессии. Наиболее часто используется метод наименьших квадратов (МНК). Его суть заключается в следующем требовании: искомые теоретические значения результативного признака 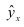должны быть такими, при которых бы обеспечивалась минимальная сумма квадратов их отклонений от эмпирических значений, т.е.

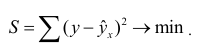
Поставив данное условие, легко определить, при каких значениях 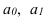и т.д. для каждой аналитической кривой эта сумма квадратов отклонений будет минимальной. Данный метод уже использовался нами в теме 6 «Статистическое изучение динамики ВЭД», поэтому, воспользуемся формулой (74) для нахождения параметров теоретической линии регрессии, заменив параметр t на x:

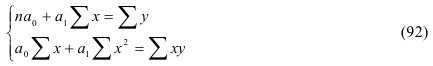
Выразив из первого уравнения системы (92) 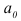, получим (*параметры a0 и a1 можно получить не только методом подстановки как приводится далее, но и методом определителей 2- го порядка) :

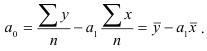
Подставив (93) во второе уравнение системы (92), затем разделив обе его части на n, получим:

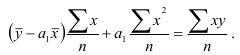
Применяя 3 раза формулу средней арифметической, получим:

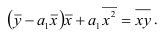
Раскрыв скобки и перенеся члены без 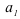в правую часть уравнения, выразим :

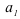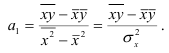
Параметр 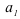в уравнении линейной регрессии называется коэффициентом регрессии, который показывает на сколько изменяется значение результативного признака y при изменении факторного признака x на единицу. Исходные данные и расчеты для нашего примера представим в таблице 19.

Таблица 19. Вспомогательные расчеты для нахождения уравнения регрессии

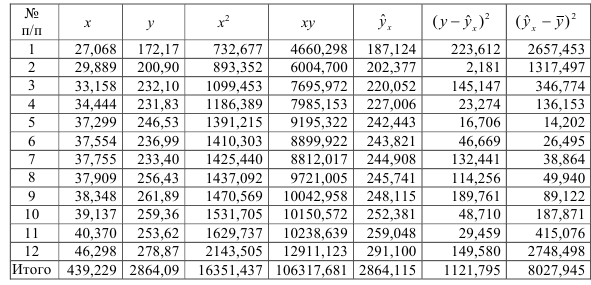
По формуле (96):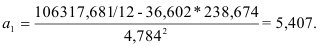
По формуле (93):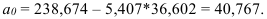

Отсюда получаем уравнение регрессии: 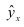=40,767+5,407x, подставляя в которое вместо x эмпирические значения факторного признака (2-й столбец таблицы 19), получаем выравненные по прямой линии теоретические значения результативного признака 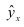(6-й столбец таблицы 19) (*сумма эмпирических (2864,09) и выравненных по прямой линии (2864,115) значений должна совпадать, но в нашем случае этого не происходит из-за округлений расчетов до 3-х знаков после запятой). Для иллюстрации различий между эмпирическими и теоретическими линиями регрессии построим график (рисунок 9).

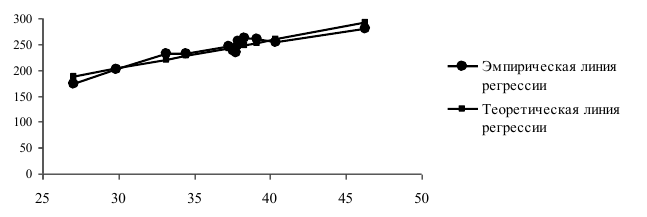
Рис. 9. График эмпирической и теоретической линий регрессии

Из рисунка 9 видно, что небольшие различия между эмпирической и теоретической линиями регрессии существуют, поэтому необходимо оценить существенность коэффициента регрессии и уравнения связи, для чего определяют среднюю ошибку параметров уравнения регрессии и сравнивают их с этой ошибкой.

Расчет ошибок параметров уравнения регрессии основан на использовании остаточной дисперсии, характеризующей расхождение (отклонение) между эмпирическими и теоретическими значениями результативного признака. Для линейного уравнения регрессии 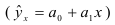средние ошибки параметров 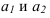определяются по формулам (97) и (98) соответственно:

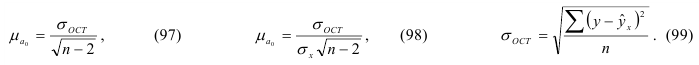
Значимость параметров проверяется путем сопоставления его значения со средней ошибкой. Обозначим это соотношение как t:

При большом числе наблюдений (n>30) параметр 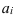считается значимым, если 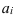t >3. Если выборка малая (n<30), то значимость параметра ai проверяется путем сравнения с табличным значения t-критерия Стьюдента при числе степеней свободы ν=n-2 и заданном уровне значимости α (Приложение 2). Если рассчитанное по формуле (100) значение больше табличного, то параметр считается значимым.

В нашем примере по формуле (99):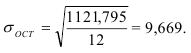
Находим среднюю ошибку параметра 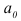по формуле (97):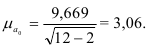
Теперь находим среднюю ошибку параметра 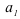по формуле (98):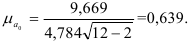
Теперь по формуле (100) для параметра :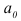
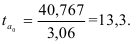
И по той же формуле для параметра :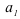

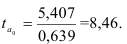
Так как выборка малая, то задавшись стандартной значимостью α=0,05 находим в 10-й строке Приложения 2 табличное значение 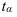=2,23, которое значительно меньше полученных значений 13,3 и 8,46, что свидетельствует о значимости обоих параметров уравнения регрессии. Наряду с проверкой значимости отдельных параметров осуществляется проверка значимости уравнения регрессии в целом или, что то же самое, проверка адекватности модели с помощью критерия Фишера по Приложению 3. Данный метод уже использовался нами для проверки адекватности уравнения тренда в предыдущей теме, поэтому воспользовавшись формулой (76) в нашем примере получим (*в числителе – сумма последнего столбца, а в знаменателе – сумма предпоследнего столбца таблицы 19) : 71,56 (2 1)1121,795 (12 2)8027,945    FР 

Сравнивая расчетное значение критерия Фишера Fр = 71,56 с табличным Fт = 4,96, определяемое по Приложению 3 при числе степеней свободы ν1 = k – 1 = 2 –1 = 1 и ν2 = n – k = 12 – 2 = 10 (т.е. 1-й столбец и 10-я строка) и стандартном уровне значимости α=0,05, можно сделать вывод, что уравнение регрессии значимо.

6. Коэффициент эластичности показывает, на сколько процентов изменяется в среднем результативный признак y при изменении факторного признака x на 1%. Он рассчитывается на основе уравнения регрессии:

где x yx  ˆ – первая производная уравнения регрессии y по x. Коэффициент эластичности – величина переменная, т.е. изменяется с изменением значений фактора x. Так, для линейной зависимости y a a x x 0 1 ˆ   :

Применительно к рассмотренному уравнению регрессии, выражающему зависимость величины таможенных платежей в федеральный бюджет от величины стоимостного внешнеторгового оборота ( x y ˆ = 40,767 + 5,407x), коэффициент эластичности по формуле (102): x x Э 40,767 5,407 5,407   .

Подставляя в данное выражение разные значения x, получаем и разные значения Э. Так, например, при x = 40 коэффициент эластичности 40,767 5,407*40 5,407*40  Э  = 0,84, а при x = 50 соответственно 40,767 5,407*50 5,407*50  Э  = 0,87 и т.д. Это значит, что при увеличении внешнеторгового товарооборота x с 40 до 40,4 млрд.долл. (т.е. на 1%), величина таможенных платежей возрастет в среднем на 0,84% прежнего уровня; при увеличении x с 50 до 50,5 млрд.долл. (т.е. на 1%) y возрастет на 0,87% и т.д.

Возможно эта страница вам будет полезна:

Задачи статистики: предмет, метод, теория

Индексы, индивидуальные индексы

Индекс – относительная величина, показывающая, во сколько раз уровень изучаемого явления в данных условиях отличается от уровня того же явления в других условиях. В статистическом анализе индексы используются не только для сопоставления уровней явлений, но и для установления значимости причин, вызывающих их изменение.

Если анализируются простые явления или не имеет значения структура сложных явлений, то применяются индивидуальные индексы. Например, такие простые явления как количество проданного товара q и его цена р своим произведением образуют такое сложное явление, как выручка от продаж Q=qp. Сравнение их значений по отдельности для конкретного товара в отчетном периоде времени относительно какого-либо базисного периода и дает индивидуальные индексы:

—количества товара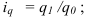
—его цены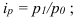
—выручки от продаж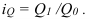

Очевидно, что индивидуальный индекс сложного явления формируется из таких индексов простых его составляющих по типологической формуле его определения. То есть

Подставив сюда индивидуальный индекс выручки, записываем: 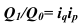откуда получаем, что

Формула (104) представляет собой двухфакторную мультипликативную модель сложного явления, позволяющую находить его изменение под влиянием каждого фактора в отдельности.

Мультипликативной она называется потому, что содержит только действие умножения. Если в формуле только сложение, или вычитание, или оба этих действия, то она называется аддитивной моделью. Если в формуле только деление, то она называется кратной моделью. Если в формуле сложение и вычитание с умножением и делением в любом сочетании, то она называется смешанной моделью.

Общее изменение выручки равняется 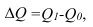а ее изменение от каждого фактора определяется следующим образом. От изменения количества товара при постоянной цене 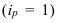оно равно

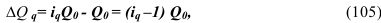
а при изменении еще и цены оно будет равным

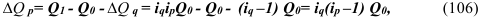
Так, если выручка от продаж возросла с 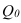= 8 млн. руб. в предыдущем периоде до 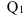=12,18 млн. руб. в последующем при увеличении количества проданного товара на 5% (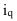=1,05) и повышении цены на 45% (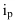=1,45), то можно по формуле (104) записать, что

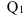= 1,05*1,45*8 = 12,18 млн. руб.

При этом весь прирост выручки в сумме 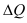= 12,18-8=4,18 млн. руб. вызван увеличением обоих факторов. За счет изменения количества проданного товара он по формуле (105) составил 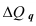=(1,05- 1)8=0,4 млн. руб., а за счет изменения цены по формуле (106) равняется 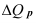=1,05(1,45-1)8 =3,78 млн. руб. Для контроля отмечаем, что сумма факторных изменений выручки равна общему: 0,4+3,78=4,18 млн. руб.

Формулы (105) и (106) получены исходя из того, что в основной формуле выручки количество товара — первый фактор, а цена — второй. Если эти факторы поменять местами, то выручка и ее общее изменение останутся прежними, но изменения от каждого фактора будут другими.

Так, если основываться на формуле выручки вида Q = pq, то ее изменение за счет цены, как первого фактора, по аналогии с формулой (105) будет равняться

Изменение выручки за счет количества товара, как второго фактора, по аналогии с формулой (106) определится по выражению

Суммарное по факторам изменение выручки по-прежнему равняется ее общему изменению.

В рассмотренном примере, считая цену первым фактором и применяя формулу (107), определяем, что изменение выручки за счет повышения цены равняется 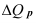= (1,45-1)8 = 3,6 млн. руб.

Изменение выручки за счет увеличения количества проданного товара, как второго фактора, по формуле (108) равно 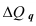= 1,45(1,05-1)8 = 0,58 млн. руб.

Общее изменение выручки осталось прежним: 3,6+0,58=4,18 млн. руб.

В связи с различными факторными изменениями выручки в зависимости от места фактора в ее основной формуле, встает вопрос, какую же формулу выручки применять для анализа. Это зависит от конкретной экономической ситуации. Если увеличение выручки обеспечивается главным образом за счет роста количества проданного товара при более или менее стабильной цене, то товар считается первым фактором, а цена — вторым. Если же увеличение выручки достигается в основном повышением цен без увеличения и даже при снижении количества проданного товара, то цена считается первым фактором, а товар — вторым.

Значит, очередность анализа по факторам вытекает из вида формулы сложного явления. Так, если материальные затраты М на выпуск продукции определяются как произведение ее количества q, удельного расхода материала m и его цены р, то типологическая формула имеет вид

М = qmp, (109)

а трехфакторная мультипликативная модель запишется как

Следовательно, можно записать следующие формулы факторных изменений материальных затрат;

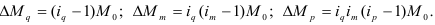
Меняя факторы местами в основной формуле (110), можно получать другие факторные формулы. Но всегда общее изменение материальных затрат, равное сумме факторных изменений, будет одинаковым.

Подобные мультипликативные модели можно формировать для неограниченного числа факторов.

Простые общие индексы

Индекс становится общим, когда в основной формуле показывается неоднородность изучаемого явления. Например, анализируется изменение выручки от продаж не одного, а всех или нескольких видов товаров. Тогда общий индекс количества проданных товаров будет равен

Аналогично по ценам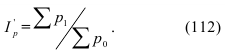

Аналогично по выручке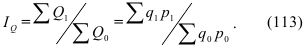

Однако здесь двухфакторная мультипликативная модель не может выглядеть как в случае индивидуальных индексов, потому что произведение простых общих индексов количества товаров и цен не равно общему индексу выручки. То есть 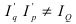и убеждаемся в этом неравенстве, подставив значения общих индексов из формул (111) – (113).

В самом деле: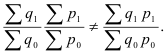

Как видим, в числителе и знаменателе левой части произведения сумм, а в числителе и знаменателе правой части сумма произведений и они, конечно, не адекватны.

Это вызвано тем, что записанные выше общие индексы простых явлений не отражают взаимосвязи между собой в сложном явлении и потому считаются не объективными. Поэтому они помечены штрихом и названы простыми общими индексами.

Агрегатные общие индексы

Объективность общим индексам придает их запись в агрегатном виде, предложенная Ласпейресом и Пааше.

Агрегатный общий индекс Ласпейреса для количества товаров как первого фактора выручки определяется по формуле

Аналогично можно записать агрегатный общий индекс Ласпейреса для цен как первого фактора выручки, то есть

В формулах Ласпейреса знаменатели по существу одинаковые, представляя собой выручку базисного периода, а числители разные. В формуле (114) это отчетная выручка в базисных ценах (количесгво товаров отчетное, а цены — базисные), в формуле (115) наоборот — базисная выручка в отчетных ценах (цены отчетные, а количество товаров — базисное).

Агрегатные общие индексы Пааше применяются ко вторым факторам мультипликативных моделей. Поэтому такой индекс для цен как второго фактора выручки определяется по формуле

Аналогично можно записать агрегатный общий индекс Пааше для количества товаров как второго фактора выручки, то есть

В формулах Пааше числители по существу одинаковые, представляя собой выручку отчетного периода, а знаменатели аналогичны числителям формул Ласпейреса. Для облегчения запоминания студентами формул Ласпейреса и Пааше предлагаю обратить внимание на букву «ш» в слове «Пааше», которая напоминает «111» — так обозначены отчетные периоды в общей формуле (две единицы – в числителе, а одна – в знаменателе). В формуле же Ласпейреса – три нуля (наоборот к формуле Пааше).

Произведения количественного индекса Ласпейреса и ценового индекса Пааше, а также ценового индекса Ласпейреса и количественного индекса Пааше дают общий индекс выручки

Однако вид этих формул показывает, что однофакторные индексы Ласпейреса и Пааше не равны между собой. То есть не равными являются количественные индексы Ласпейреса и Пааше и ценовые. Американский экономист Гершенкрон обширными расчетами установил, что по одному и тому же фактору индекс Ласпейреса обычно больше индекса Пааше и это открытие названо эффектом Гершенкрона.

Но в статистике должно быть одно значение индекса, поэтому американский экономист Фишер предложил применять среднюю геометрическую величину из индексов Ласпейреса и Пааше, определяя ее по формулам:

для количества товаров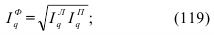

для цен

Общие индексы как средние из индивидуальных

Помимо записи общих индексов в агрегатном виде, на практике часто используют формулы их расчета как величин, средних из соответствующих индивидуальных индексов. Используя их формулы, можем записывать, что 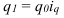и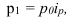 а также, что 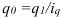и 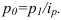Подставив отчетные значения количества товара и цены в формулу общего индекса выручки, получим

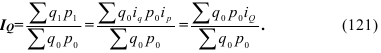
Значит, общий индекс выручки можно определять только через ее базисные значения с умножением в числителе на индивидуальный индекс выручки по конкретному товару.

Теперь подставим базисные значения количества товара и цены в формулу общего индекса выручки. Тогда получим

Значит, общий индекс выручки можно определять только через ее отчетные значения с делением в знаменателе на индивидуальный индекс выручки по конкретному товару.

Аналогично через индивидуальные индексы количества товара и цены можно выразить агрегатные общие индексы Ласпейреса и Пааше.

Индекс структурных сдвигов

Выше изложенные общие индексы применимы к изучению явлений, образованных как разными, так и однородными процессами. В последнем случае динамику итога можно показать через простые общие индексы отдельных факторов.

Для доказательства в формуле количественного индекса Ласпейреса числитель умножим и разделим на 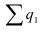, а знаменатель – на 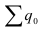. Тогда будем иметь

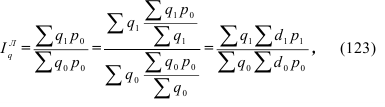
где 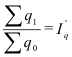— простой общий индекс количества товаров;
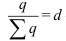– доля или удельный вес конкретного товара в общем количестве;
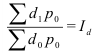— агрегатный общий индекс структуры, доли или удельного веса, часто называемый индексом структурных сдвигов.

Следовательно, количественный индекс Ласпейреса равняется произведению простого общего индекса количества товаров и индекса структурных сдвигов. То есть

откуда для определения индекса структурных сдвигов получается довольно простая формула

Используя формулу (124) в двухфакторной модели общего индекса выручки, получим его трехфакторную мультипликативную модель вида

Трехфакторная модель возможна к широкому применению в экономическом анализе для установления количественного влияния каждого фактора на вариацию сложного явления.

Факторный анализ общей и частной выручки

Приравнивая правую часть полученной трехфакторной модели и среднюю часть формулы (113), записываем выражение

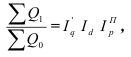
из которого заключаем, что общую выручку отчетного периода можно определить через общую выручку базисного периода и общие индексы по мультипликативной формуле

Эта формула в точности соответствует мультипликативной модели (110), что позволяет применять соответствующие формулы факторных изменений. Так, изменение общей выручки за счет изменения общего количества товаров определится по формуле

Изменение общей выручки за счет изменения долей конкретных товаров (структурных сдвигов) определяется по формуле

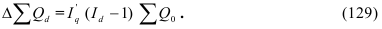
И наконец изменение общей выручки за счет изменения цен определяется по формуле

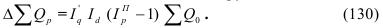
Естественно, сумма факторных изменений должна равняться общему итоговому изменению. То есть для контроля правильности анализа проверяется выполнение условия

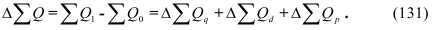
Факторный анализ изменения выручки по отдельному товару в составе общего товарооборота ведется на основе следующей трехфакторной мультипликативной модели

где 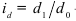— индивидуальный индекс доли конкретного товара.

Следовательно, изменения выручки по конкретному товару за счет изменения каждого фактора могут определяться по формулам:

за счет изменения общего количества товаров (товарооборота)

за счет изменения доли конкретного товара

за счет изменения цены конкретного товара

Естественно, факторные изменения выручки по конкретному товару в сумме должны равняться полному изменению выручки по этому товару. То есть для контроля правильности анализа проверяется выполнение условия

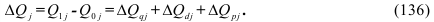
где j — признак конкретного товара.

Кроме того, полные изменения выручки по каждому товару в сумме должны равняться общему изменению выручки по всему товарообороту. То есть для контроля правильности анализа дополнительно проверяется выполнение условия 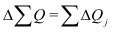. При этом для облегчения необходимого контроля результаты факторного анализа представляются в виде факторной таблицы, рассмотренной ниже в методических указаниях по теме.

Индексы фиксированного (постоянного) и переменного состава

В полученной трехфакторной модели (126) второй и третий индексы запишем подробно по формулам их определения, а третий еще и сократим на 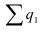. Тогда сначала будем иметь

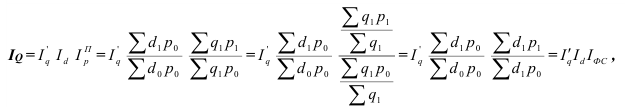
а, произведя очевидное сокращение и обозначив

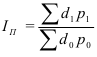— индекс переменного состава, (137) получим общий индекс выручки в виде формулы

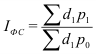называется индексом фиксированного (постоянного) состава. (139)

Следовательно, общий индекс выручки есть произведение простого общего индекса количества товаров и индекса переменного состава, который показывает изменение средних цен, т.е.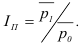

Из формулы (138) можно заключить, что индекс переменного состава есть частное от деления общего индекса выручки на простой общий индекс количества товаров, тогда как ценовый индекс Пааше наравне с формулой (116) возможно определять как отношение общего индекса выручки и количественного индекса Ласпейреса. Изложенные математические выкладки позволяют общий индекс выручки определять следующими семью способами

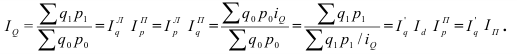
Результат расчета любым способом должен быть одинаковым и это яркий пример того, что истина всегда одна, хотя пути ее достижения могут быть разными.

Контрольная работа 8.

Процесс определения всевозможных индексов и факторного анализа сложного явления рассмотрим на примере двух фирм, выпускающих однородный продукт. Исходные данные приведены в табл. 20.

Решение:

В табл. 20 итоговое количество продукта есть сумма его количества по фирмам, а итоговая цена представляет собой среднюю арифметическую взвешенную величину, найденную по формуле (11).

Таблица 20. Результаты работы двух фирм по выпуску однородного продукта

Так, для базисного периода она равна

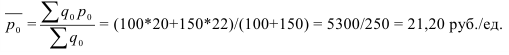
Для отчетного периода средняя цена равняется

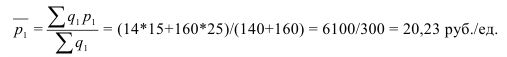
После этого в табл. 21 ведется расчет индивидуальных индексов.

Таблица 21. Определение выручки и индивидуальных индексов

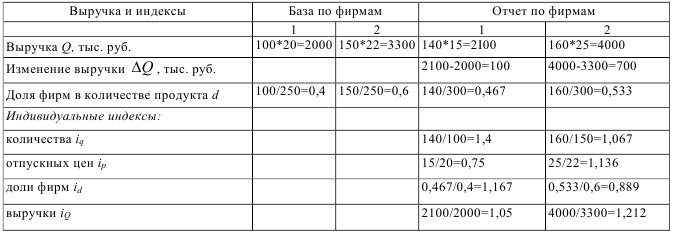
Из табл. 21 заключаем, что общая выручка по периодам составляет:

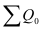= 2000+3300 =5300 тыс. руб.; 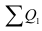= 2100+4000 =6100 тыс. руб.

Ее абсолютное изменение равно 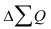=6100-5300=800 тыс. руб., а общий индекс изменения равняется 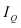= 6100/5300 = 1,151.

Контроль правильности расчетов по табл. 21 заключается в следующем.

1. Общее изменение выручки должно равняться сумме ее частных изменений: 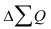= 100+700 = 800 тыс. руб.
2. Произведение факторных индивидуальных индексов по периодам должно равняться соответствующему индивидуальному индексу выручки: 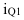=1,4*0,75 =1,05; 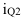= 1,067*1,136 = 1,212.
3. Сумма долей количества продукта по периодам должна равняться единице: 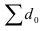=0,4+0,6 = 1; 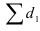=0,467+0,533=1.

Затем переходим к расчету простых и агрегатных общих индексов. Простой общий индекс количества продукта — по формуле (111) 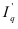=(140+160)/(100+150)=300/250=1,2.

Агрегатный общий количественный индекс Ласпейреса — по формуле (114)

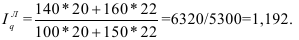
Агрегатный общий ценовый индекс Пааше — по формуле (116)

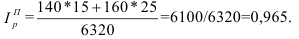
Контроль по формуле 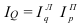= 1,192*0,965 = 1,151.

Агрегатный общий ценовый индекс Ласпейреса — по формуле (115)

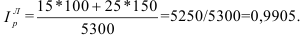
Агрегатный общий количественный индекс Пааше — по формуле (117) 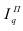=6100/5250=1,162.

Контроль по формуле 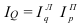= 0,9905*1,162 =1,151.

Средняя геометрическая величина из индексов Ласпейреса и Пааше (по методике Фишера) по формулам (119) и (120)

Общий индекс выручки как средний из ее индивидуальных индексов:

— с использованием только базисной выручки — по формуле (121)

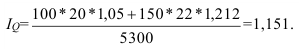
— с использованием только отчетной выручки — по формуле (122)

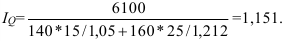
Индекс структурных сдвигов — по формуле

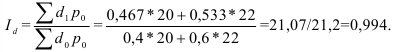
Контроль по формуле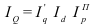= 1,2*0,994*0,965 = 1,151.

Индекс переменного состава — по формуле (137)

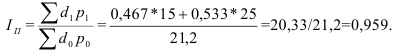
Контроль по формуле 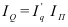= 1,2*0,959=1,151.

Далее выполняется факторный анализ общей выручки. Так ее изменение за счет изменения общего количества продукта определится по формуле (128) 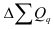= (1,2-1)*5300 = 1060 тыс. руб.

Изменение общей выручки за счет структурных сдвигов в количестве продукта находится по формуле
(129) 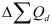= 1,2*(0,994-1)*5300 = -40 тыс. руб.

Изменение общей выручки за счет изменения отпускных цен — по формуле (130)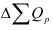
=1,2*0,994*(0,965-1)*5300 = -220 тыс. руб.

Контроль по формуле (131): 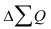= 1060-40-220 = 800 тыс. руб.

Результаты факторного анализа общей выручки заносятся в табл. 22.

Наконец, ведется факторный анализ изменения частной выручки по формулам (133) – (135). Так у первой фирмы изменение выручки за счет изменения общего количества продукта равно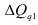
=(1,2-1)*2000 = 400 тыс. руб.

Аналогично у второй фирмы 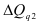= (1,2-1)*3300 = 660 тыс. руб. Контроль: 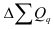=400+660=1060 тыс.руб.

У первой фирмы изменение выручки за счет структурных сдвигов в количестве продукта равно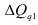
=1,2*(1,167-1)*2000 = 400 тыс. руб.

Аналогично у второй фирмы 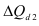=1,2*(0,889-1)*3300 = -440 тыс. руб.
Контроль: 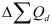=400-440= -40 тыс.руб.

У первой фирмы изменение выручки за счет изменения отпускной цены равно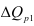
=1,2*1,167*(0,75-1)*2000 = -700 тыс. руб.

Аналогично у второй фирмы 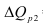=1,2*0,889*(1,136-1)*3300 = 480 тыс. руб.
Контроль: 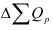= -700+480= -220 тыс.руб.

Результаты факторного анализа частной выручки также заносятся в табл. табл. 23, в которой все числа оказались взаимно согласованными.

Таблица 22. Результаты факторного анализа сложного явления

Таблица. 23 свидетельствует о правильности проведенного факторного анализа, поскольку в ней факторные изменения выручки, как по столбцам, так и по строкам в сумме равняются ее изменениям по отдельным факторам, фирмам и в целом.

Приложения – статистические таблицы

Приложение 1. Значения интеграла Лапласа