Заказать эконометрику — решение на заказ онлайн

Здравствуйте! Я Людмила Анатольевна Фирмаль, занимаюсь помощью студентам более 17 лет. У меня своя команда грамотных, сильных преподавателей. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И неважно – она по объёму на две формулы или огромная, сложно структурированная, на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте.

Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!

Как заказать выполнение заданий по эконометрике

Вы можете написать сообщение в WhatsApp. После этого я оценю ваш заказ и укажу стоимость и срок выполнения вашей работы. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за вашу работу, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл готовой работы в личные сообщения.

Сколько может стоить заказ эконометрики

Стоимость заказа зависит от задания и требований Вашего учебного заведения. На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости, загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.

Какой срок выполнения заказа

Минимальный срок выполнения заказа составляет 2-4 дня, но помните, срочные задания оцениваются дороже.

Как оплатить заказ

Сначала пришлите задание, я оценю, после вышлю вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.

Гарантии и исправление ошибок

В течение 1 года с момента получения Вами готового решения заказа действует гарантия. В течении 1 года я и моя команда исправим любые ошибки в заказе.

Чуть ниже я предоставила примеры оформления заказов по некоторым темам эконометрики, так я буду оформлять ваши работы если закажите у меня, это не все темы, это лишь маленькая часть их, чтобы вы понимали насколько подробно я оформляю.

Пример оформления заказа №1.

По территориям региона приводятся данные за 199Х г.

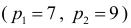
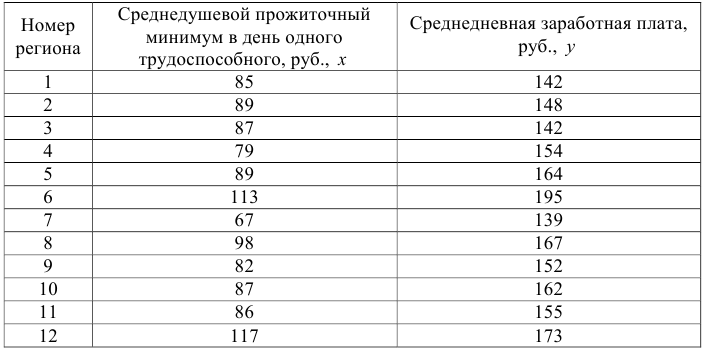
Требуется:

1. Построить линейное уравнение парной регрессии 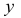по .
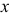2. Рассчитать линейный коэффициент парной корреляции, коэффициент детерминации и среднюю ошибку аппроксимации.
3. Оценить статистическую значимость уравнения регрессии в целом и отдельных параметров регрессии и корреляции с помощью 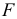-критерия Фишера и 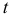-критерия Стьюдента.
4. Выполнить прогноз заработной платы 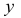при прогнозном значении среднедушевого прожиточного минимума 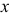, составляющем 107% от среднего уровня.
5. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.
6. На одном графике отложить исходные данные и теоретическую прямую.
7. Проверить вычисления в MS Excel.

Решение:

1.Для расчета параметров уравнения линейной регрессии строим расчетную таблицу.

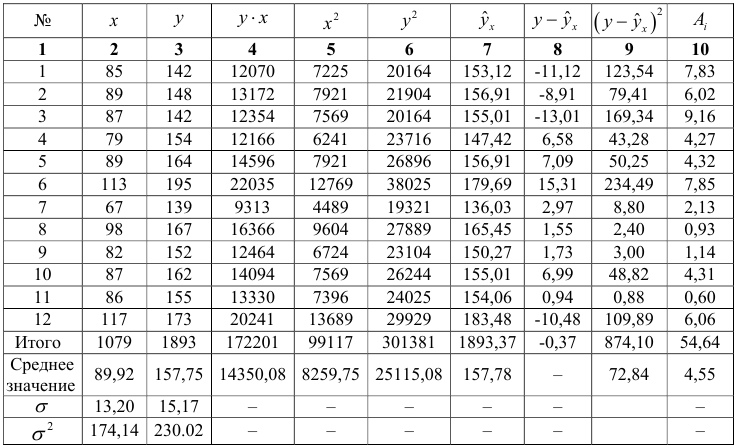
Находим параметры уравнения регрессии

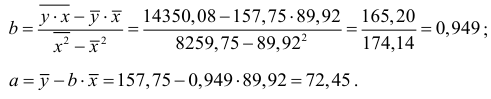
Получено уравнение регрессии:

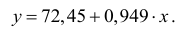
Параметр регрессии позволяет сделать вывод, что с увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,95 руб. (или 95 коп.).

После нахождения уравнения регрессии заполняем столбцы 7-10 нашей таблицы.

• Тесноту линейной связи оценит коэффициент корреляции:

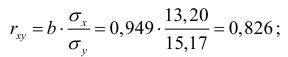
Т.к. значение коэффициента корреляции больше 0,7, то это говорит о наличии весьма тесной линейной связи между признаками. Коэффициент детерминации:

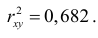
Это означает, что 68,2% вариации заработной платы (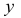) объясняется вариацией фактора 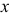— среднедушевого прожиточного минимума.

Качество модели определяет средняя ошибка аппроксимации:

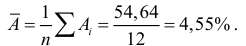
Качество построенной модели оценивается как хорошее, так как 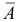не превышает 10%.

• Оценку статистической значимости уравнения регрессии в целом проведем с помощью 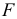-критерия Фишера. Фактическое значение 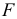-критерия составит

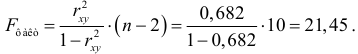
Табличное значение критерия при пятипроцентном уровне значимости и степенях свободы

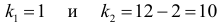
составляет 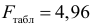. Так как 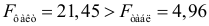, то уравнение регрессии признается статистически значимым.

Оценку статистической значимости параметров регрессии и корреляции проведем с помощью 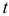-статистики Стьюдента и путем расчета доверительного интервала каждого из параметров.

Табличное значение 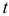-критерия для числа степеней свободы

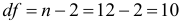
и уровня значимости 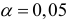составит .

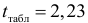Определим стандартные ошибки 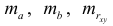(остаточная дисперсия на одну степень свободы

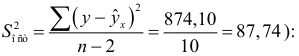
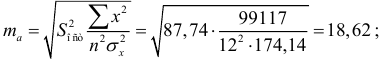
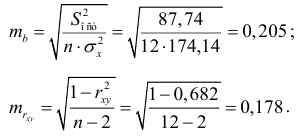
Тогда

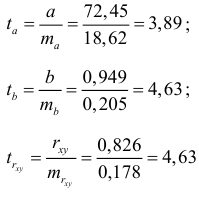
Фактические значения 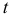-статистики превосходят табличное значение:

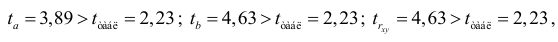
поэтому параметры 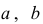и 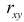не случайно отличаются от нуля, а статистически значимы.

Рассчитаем доверительные интервалы для параметров регресси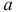и и 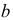. Для этого определим предельную ошибку для каждого показателя:

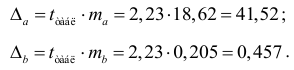
Доверительные интервалы

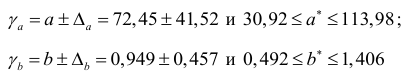
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью 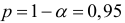параметры 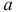и 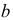, находясь в указанных границах, не принимают нулевых значений, т.е. являются статистически значимыми и существенно отличны от нуля.

Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:

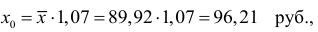
тогда индивидуальное прогнозное значение заработной платы составит:

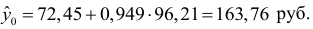
Ошибка прогноза составит:

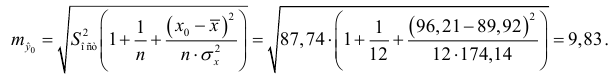
Предельная ошибка прогноза, которая в 95% случаев не будет превышена, составит:

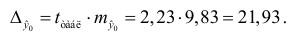
Доверительный интервал прогноза:

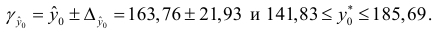
Выполненный прогноз среднемесячной заработной платы является надежным

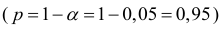
и находится в пределах от 141,83 руб. до 185,69 руб.

В заключение решения задачи построим на одном графике исходные данные и теоретическую прямую:

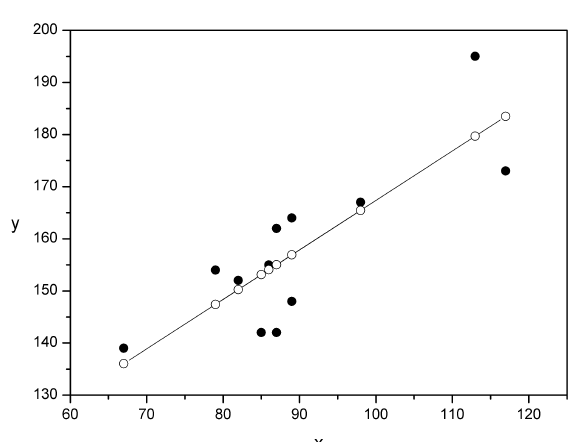
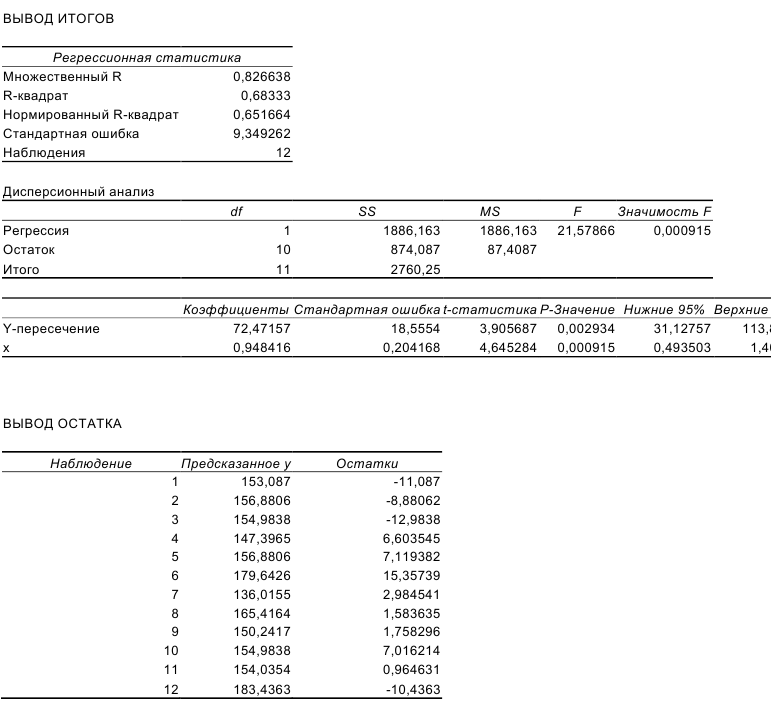
Проверим вычисления в MS Excel (Сервис—^Анализ данных—>Регрессия).

Получаем следующие результаты:

Пример оформления заказа №2.

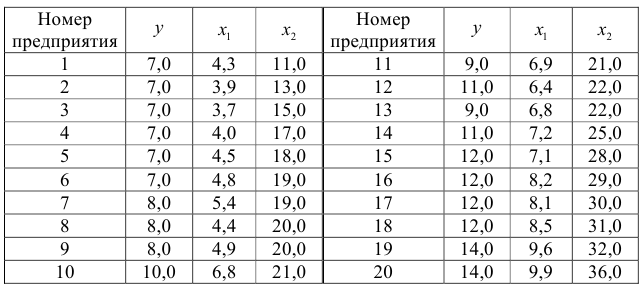
По 20 предприятиям региона изучается зависимость выработки продукции на одного работника 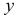(тыс. руб.) от ввода в действие новых основных фондов 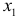(% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих (%).

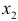Требуется:

1. Построить линейную модель множественной регрессии. Записать стандартизованное уравнение множественной регрессии. На основе стандартизованных коэффициентов регрессии и средних коэффициентов эластичности ранжировать факторы по степени их влияния на результат.
2. Найти коэффициенты парной, частной и множественной корреляции. Проанализировать их.
3. Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации.
4. С помощью 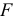-критерия Фишера оценить статистическую надежность уравнения регрессии и коэффициента детерминации .
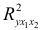5. С помощью 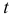-критерия оценить статистическую значимость коэффициентов чистой регрессии.
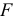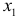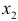6. С помощью частных -критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора после и фактора 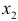после .
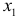7. Составить уравнение линейной парной регрессии, оставив лишь один значащий фактор.

Решение:

Для удобства проведения расчетов поместим результаты промежуточных расчетов в таблицу:

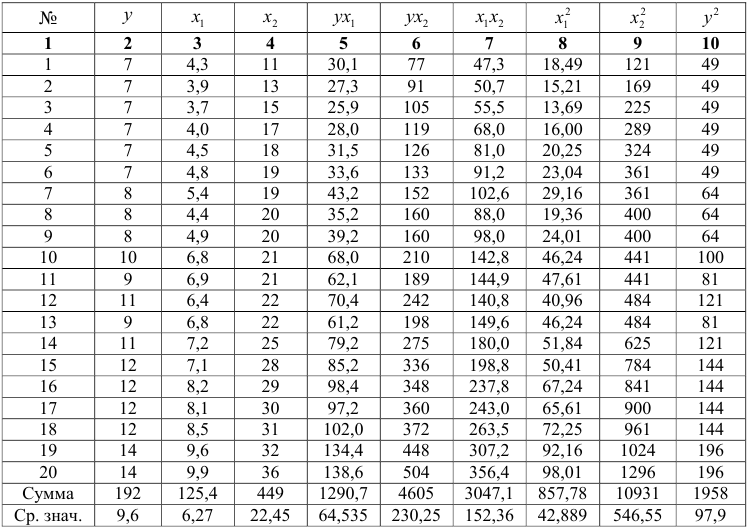
Найдем средние квадратические отклонения признаков:

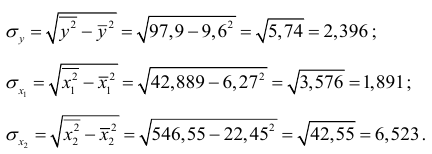
Для нахождения параметров линейного уравнения множественной регрессии

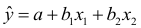
необходимо решить систему линейных уравнений относительно неизвестных параметров

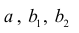
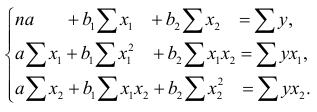
либо воспользоваться готовыми формулами

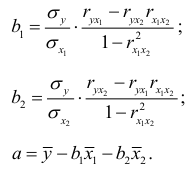
Рассчитаем сначала парные коэффициенты корреляции:

Находим коэффициенты чистой регрессии и параметр а :

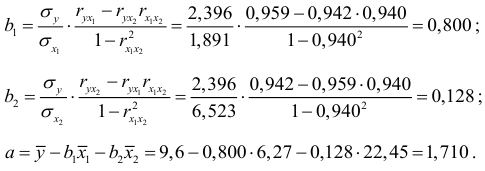
Таким образом, получили следующее уравнение множественной регрессии:

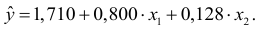
Уравнение регрессии показывает, что при увеличении ввода в действие основных фондов на 1% (при неизменном уровне удельного веса рабочих высокой квалификации) выработка продукции на одного рабочего увеличивается в среднем на 0,8 тыс. руб., а при увеличении удельного веса рабочих высокой квалификации в общей численности рабочих на 1% (при неизменном уровне ввода в действие новых основных фондов) выработка продукции на одного рабочего увеличивается в среднем на 0,128 тыс. руб.

После нахождения уравнения регрессии составим новую расчетную таблицу для определения теоретических значений результативного признака, остаточной дисперсии и средней ошибки аппроксимации.

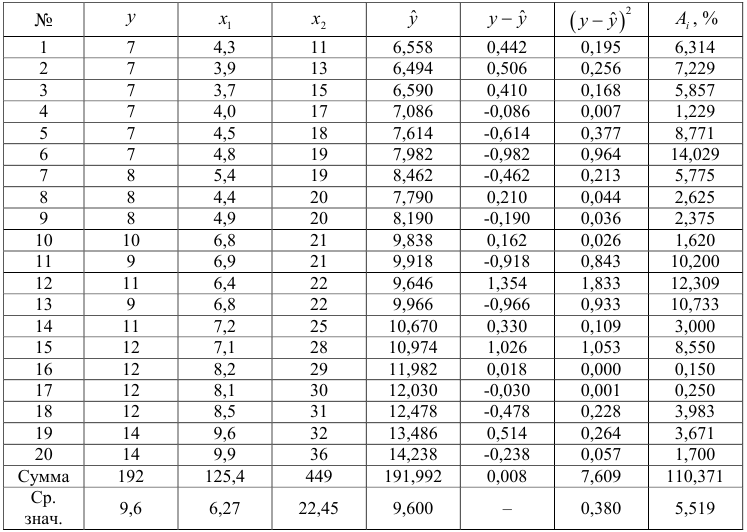
Остаточная дисперсия:

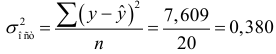
Средняя ошибка аппроксимации:

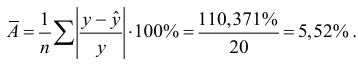
Качество модели, исходя из относительных отклонений по каждому наблюдению, признается хорошим, т.к. средняя ошибка аппроксимации не превышает 10%.

Коэффициенты 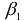и 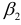стандартизованного уравнения регрессии :

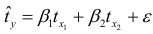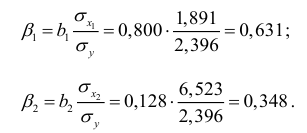
Т.е. уравнение будет выглядеть следующим образом:

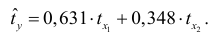
Так как стандартизованные коэффициенты регрессии можно сравнивать между собой, то можно сказать, что ввод в действие новых основных фондов оказывает большее влияние на выработку продукции, чем удельный вес рабочих высокой квалификации.

Сравнивать влияние факторов на результат можно также при помощи средних коэффициентов эластичности:

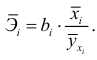
Вычисляем:

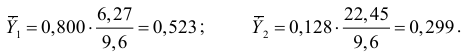
Т.е. увеличение только основных фондов (от своего среднего значения) или только удельного веса рабочих высокой квалификации на 1% увеличивает в среднем выработку продукции на 0,523% или 0,299% соответственно. Таким образом, подтверждается большее влияние на результат 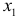фактора чем фактора .

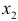• Коэффициенты парной корреляции мы уже нашли:

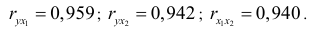
Они указывают на весьма сильную связь каждого фактора с результатом, а также высокую межфакторную зависимость (факторы 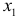и 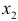явно коллинеарны, т.к. 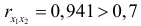). При такой сильной межфакторной зависимости рекомендуется один из факторов исключить из рассмотрения.

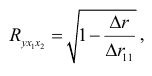
где

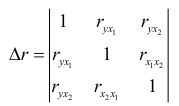
• определитель матрицы парных коэффициентов корреляции;

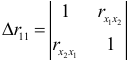
• определитель матрицы межфакторной корреляции. Находим:

Коэффициент множественной корреляции:

Аналогичный результат получим при использовании других формул:

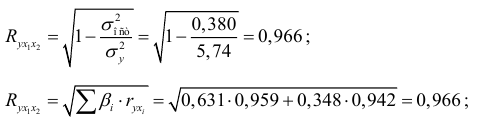
Коэффициент множественной корреляции указывает на весьма сильную связь всего набора факторов с результатом.

• Нескорректированный коэффициент множественной детерминации 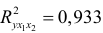оценивает долю дисперсии результата за счет представленных в уравнении факторов в общей вариации результата. Здесь эта доля составляет 93,3% и указывает на весьма высокую степень обусловленности вариации результата вариацией факторов, иными словами — на весьма тесную связь факторов с результатом.

Скорректированный коэффициент множественной детерминации

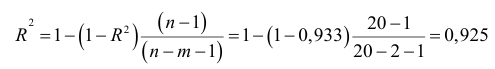
определяет тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов и поэтому может сравниваться по разным моделям с разным числом факторов. Оба коэффициента указывают на весьма высокую (более 92%) детерминированность результата у в модели факторам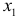и и .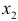

• Оценку надежности уравнения регрессии в целом и показателя тесноты связи 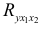, дает 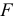-критерий Фишера:

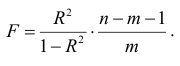
В нашем случае фактическое значение 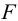-критерия Фишера:

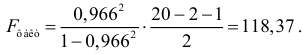
Получили, что 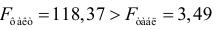(при 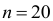), т.е. вероятность случайно получить такое значение F -критерия не превышает допустимый уровень значимости 5%. Следовательно, полученное значение не случайно, оно сформировалось под влиянием существенных факторов, т.е. подтверждается статистическая значимость всего уравнения и показателя тесноты связи .

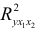• Оценим статистическую значимость параметров чистой регрессии с помощью 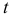-критерия Стьюдента. Рассчитаем стандартные ошибки коэффициентов регрессии:

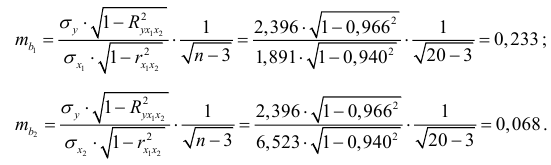
Фактические значения 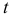-критерия Стьюдента:

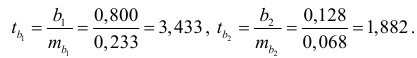
Табличное значение критерия при уровне значимости 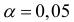и числе степеней свободы 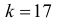составит

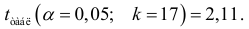
Таким образом, признается статистическая значимость параметра 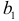и незначимость параметра .

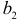Доверительные интервалы для параметров чистой регрессии:

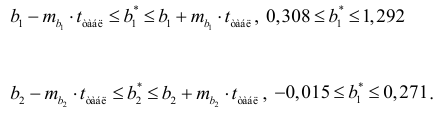
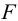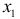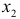• С помощью частных -критериев Фишера оценим целесообразность включения в уравнение множественной регрессии фактора после и фактора 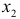после 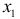при помощи формул (3.16):

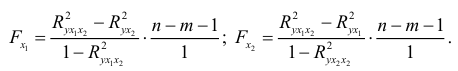
Найдем 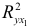и :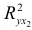

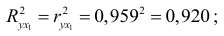
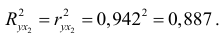
Имеем:

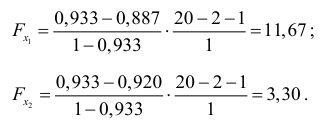
Получили, что

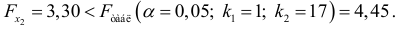
Следовательно, включение в модель фактора 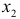после того, как в модель включен фактор 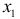, статистически нецелесообразно: прирост факторной дисперсии за счет дополнительного признака 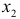оказывается незначительным, существенным; фактор 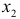включать в уравнение после фактора 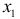не следует.

Если поменять первоначальный порядок включения факторов в модель и рассмотреть вариант включения 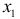после 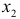, то результат расчета частного 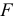-критерия для 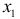, будет иным.

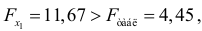
т.е. вероятность его случайного формирования меньше принятого стандарта 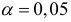(5%). Следовательно, значение частного 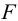-критерия для дополнительно включенного фактора 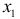не случайно, является статистически значимым, надежным, достоверным: прирост факторной дисперсии за счет дополнительного фактора 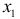является существенным. Фактор 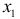должен присутствовать в уравнении, в том числе в варианте, когда он дополнительно включается после фактора .

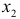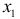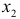• Общий вывод состоит в том, что множественная модель с факторами и с 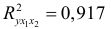содержит неинформативный фактор 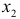. Если исключить фактор 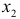, то можно ограничиться уравнением парной регрессии:

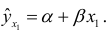
Найдем его параметры:

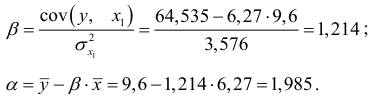
Таким образом,

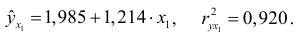
Проверим вычисления в MS Excel.

Найдем матрицу парных коэффициентов корреляции

(Сервис—^Анализ данных—^Корреляция):

С помощью инструмента Регрессия (Сервис—>Анализ данных—>Регрессия) получаем следующие результаты: вывод итогов

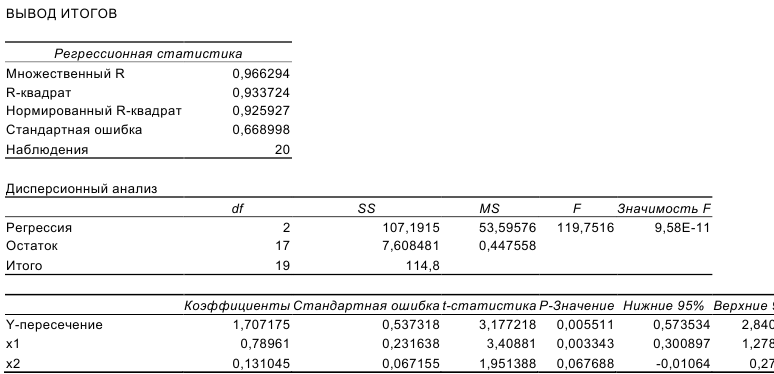
Результаты «ручного счета» от машинного отличаются незначительно (отличия связаны с ошибками округления).

Возможно эти страницы вам будут полезны:

• Примеры решения задач по эконометрике
• Курсовая работа по эконометрике
• Лабораторная работа по эконометрике
• Помощь по эконометрике
• Решение задач по эконометрике в Excel
• Системы эконометрических уравнений