Контрольные работы по экономико математическим методам

Математическое моделирование экономических процессов тесно связано с компьютеризацией экономической науки и ее практическим применением. Контрольные занятия по курсу «Экономико-математические методы и модели» предназначены для углубления теоретические знаний студентов по моделированию экономических процессов как на микро так и на макро уровне, а также для получения практических навыков построения численных моделей, их реализации с применением ПЭВМ и анализа полученных результатов.

Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!

Экономико-математические методы

Экономико-математические методы дают фундаментальную основу решения аналитических задач различных сфер деятельности современных предпринимателей. Построение математических моделей в экономике во многих случаях связано напрямую с анализом статистических данных, для получения которых часто требуются большие материальные и временные затраты. Поэтому изучение данного предмета требует от студентов глубоких знаний как в области экономики, так и математики и статистики. Реальный объект моделирования в экономике по своей сложности превосходит многие объекты физической природы. Вместе с тем проверка адекватности экономико-математических моделей с помощью единственного критерия истины – практики – затруднена, поскольку практический эксперимент зачастую связан с колоссальными затратами и поэтому не всегда возможен.

Возможно эта страница вам будет полезна:

Предмет экономико-математические методы (ЭММ)

Данный лабораторный практикум содержит варианты типовых заданий по лабораторным работам, выполнение которых предполагает использование ЭВМ и краткие инструкции для решения задач с использованием пакета EXCEL.

Контрольная работа №1. Тема: Оптимизация деятельности торгового предприятия

Цель — научить студентов:

• составлять оптимизационные модели;
• решать полученные математические задачи на ЭВМ с использованием пакета EXCEL;
• проводить содержательный послеоптимизационный анализ полученных результатов.

Постановка задачи:

Торговое предприятие (предприятие оптовой торговли), исходя из специализации, может реализовать 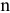групп товаров 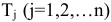. Пусть общая площадь торговых залов 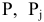— норматив складских площадей на содержание товаров 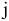-ой группы; 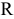— фонд рабочего времени работников, 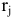— плановый норматив затрат времени работников на единицу товарооборота 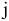-ой товарной группы. Пусть 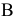— допустимые издержки обращения, 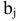— плановый норматив издержек обращения на единицу товарооборота 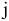-ой товарной группы. — общий объем товарных запасов. 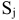— норматив товарных запасов на единицу товарооборота 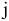-ой товарной группы. 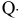— плановый показатель товарооборота, 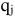— параметр товарооборота (средняя цена реализации), по 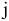-ой товарной группе. 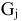— минимально допустимые значения плана товарооборота по 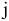-ой товарной группе. 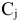— торговая прибыль в расчете на единицу товарооборота 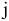-й группы. Требуется

1. определить план хозяйственной деятельности торгового предприятия, обеспечивающий максимум торговой прибыли при заданных ограничениях на складские площади, трудовые ресурсы, издержки обращения, товарные запасы, величину товарооборота и др.
2. Сделать анализ полученного решения.
3. Дать экономическую интерпретацию двойственным оценкам и дополнительным двойственным переменным.
4. Выявить «узкие места» на торговом предприятии и сделать рекомендации по их «расшивке»

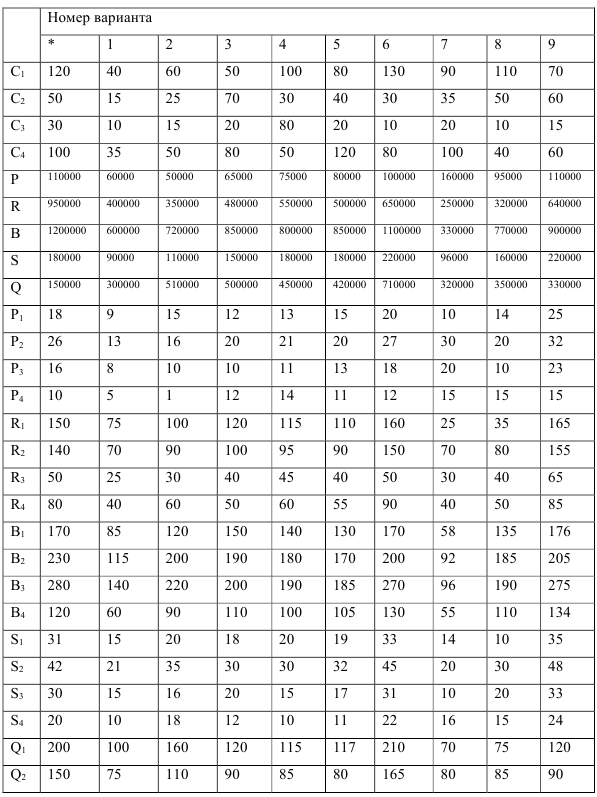
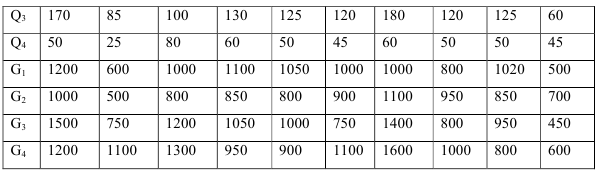
Порядок выполнения работы, (на примере варианта *)

Составление математической модели задачи. Введем переменные: 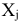(ед.)- величина товарооборота 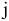-й товарной группы. Тогда математическая модель задачи примет вид:

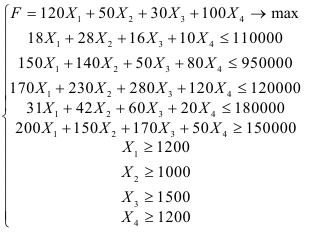
• Инструкция по решению задачи средствами EXCEL. 2.1. Ввод условий задачи.

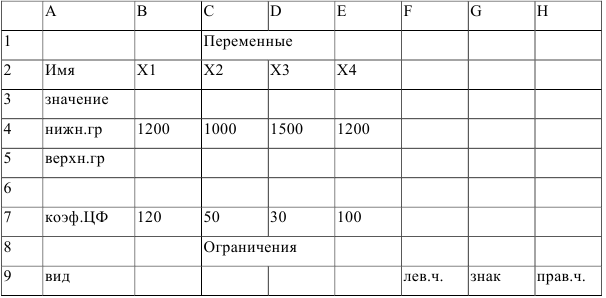
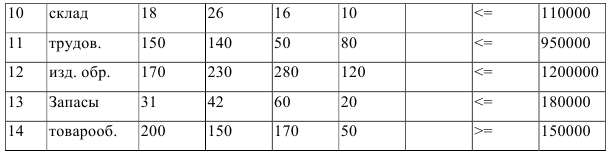
Шаг 1. Сделать форму и ввести исходные данные.

Шаг 2. Ввод зависимостей из математической модели.

Чтобы получить значение целевой функции в ячейке F7, воспользуемся функцией СУММПРОИЗВ. Для этого поместим курсор в ячейку F7, с помощью команды МАСТЕР ФУНКЦИЙ вызовем математическую функцию СУММПРОИЗВ. На экране появится диалоговое окно. В массив 1 вводим строку со значениями переменных, т.е. SB$3:$E$3 (знак $ ставим для того, чтобы адрес не менялся при копировании формул). В массив 2 ввести адрес строки коэффициентов целевой функции, т.е. В7:Е7.

Заметим, что во все диалоговые окна адреса ячеек удобно вводить не с клавиатуры, а протаскивая мышь по ячейкам, чьи адреса следует ввести.

Далее копируем формулу из ячейки F7 в столбец «Левые части ограничений».

Решение контрольной осуществляется в следующей последовательности

Командой Поиск решения из меню Сервис откроем диалоговое окно Поиск решения и занесем в него необходимые данные: Установить целевую функцию — адрес ячейки, отведенной под значение целевой функции, т.е. F7; Равной — максимальному значению;

Изменяя ячейки — адреса изменяемых значений переменных, т.е. ВЗ:ЕЗ; Ограничения — Добавить…

На экране появится диалоговое окно Добавление ограничения. Здесь вводим граничные условия на переменные: ВЗ:ЕЗ > В4:Е4 Добавить.

Вводим ограничения по ресурсам:

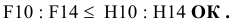
Далее командой Параметры вызываем диалоговое окно Параметры и устанавливаем флажки: Линейная модель. Неотрицательные значения, Автоматическое масштабирование. Возвращаемся в диалоговое окно Поиск решения и, щелкнув по кнопке Выполнить, находим оптимальное решение задачи. На экране появляется диалоговое окно Результаты поиска решения. Помечаем для вывода все три отчета: по результатам, по устойчивости, по пределам.

Анализ полученных результатов.

Экономико-математические методы задачи с решением и примерами

Контрольная работа №2. Тема: Оптимизация сетевого графика по времени

Цель Научиться решать задачу сетевого планирования с одновременной оптимизацией средствами EXCEL. Постановка задачи 1.

Проект представлен сетевым графиком. Для каждой работы известна ее продолжительность 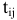и минимально возможное время выполнения 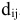. Пусть задан срок выполнения проекта 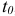, а расчетное 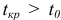. Продолжительность выполнения работы 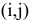линейно зависит от суммы дополнительно вложенных средств 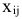и выражается соотношением: 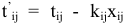. Технологические коэффициенты 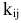известны.

Требуется найти такие 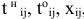, чтобы:

• срок выполнения всего комплекса работ не превышал заданной величины ;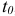

• суммарное количество дополнительно вложенных средств было минимальным.;

• продолжительность выполнения каждой работы 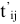была не меньше заданной величины .

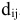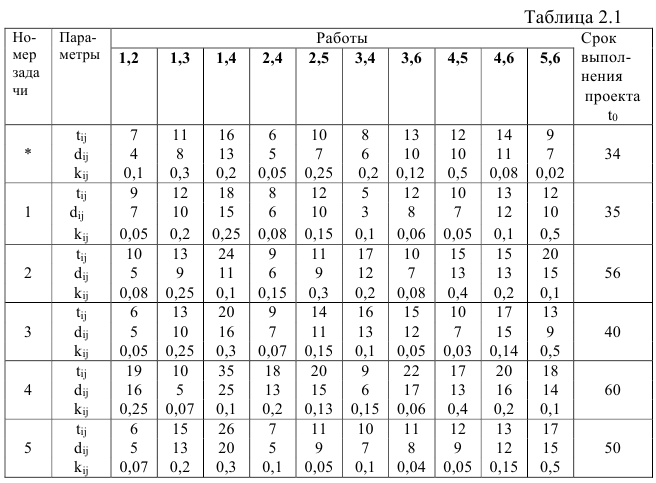
1 Запишем все данные на сетевой график и рассчитаем сроки свершения событий .

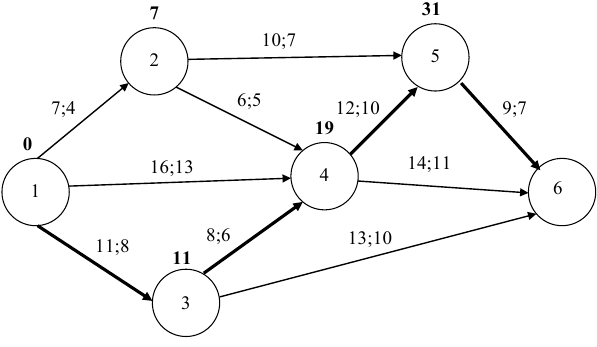
Расчеты показали, что срок выполнения проекта 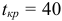, т.е. превышает директивный срок .

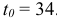• Составление математической модели задачи. Целевая функция имеет вид

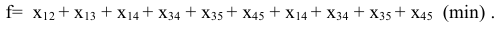
Запишем ограничения задачи:

а) срок выполнения проекта не должен превышать :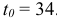

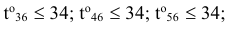
б) продолжительность выполнения каждой работы должна быть не меньше минимально возможного времени:

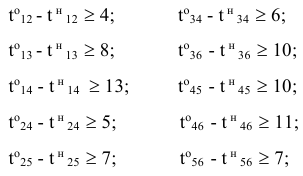
в) зависимость продолжительности работ от вложенных средств:

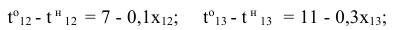
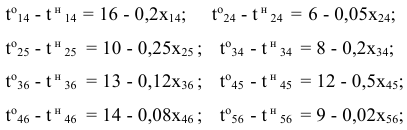
г) время начала выполнения каждой работы должно быть не меньше времени окончания непосредственно предшествующей ей работы:

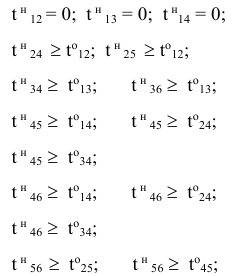
д) условие неотрицательности неизвестных:

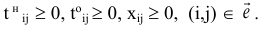
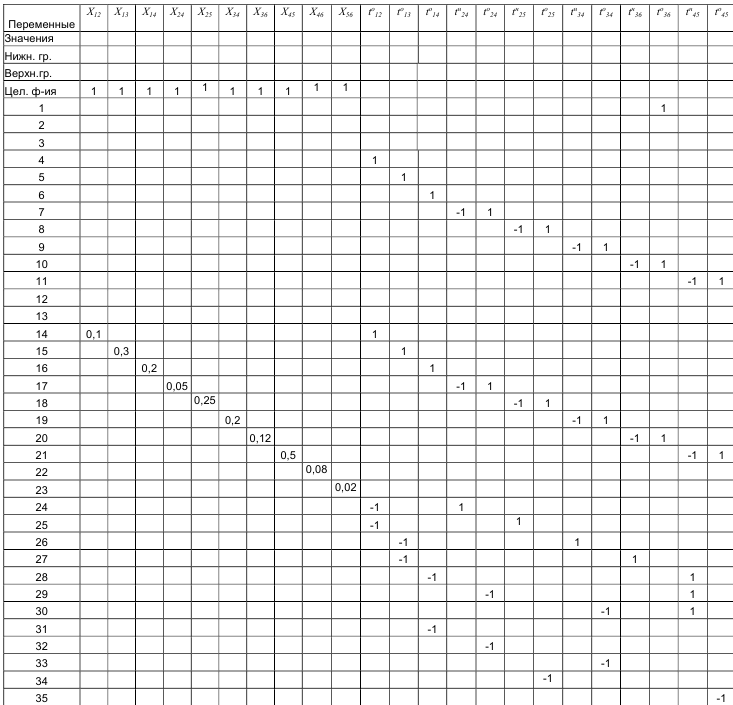
Численное решение задачи:

Табличную запись математической модели см. табл. 2.2.

Решив данную задачу средствами EXCEL, получаем следующие результаты:

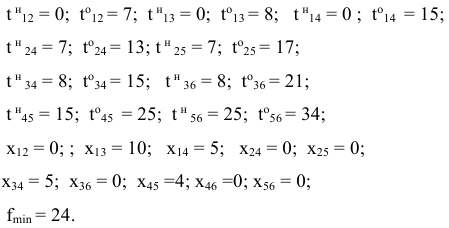
Результаты представим на сетевом графике:

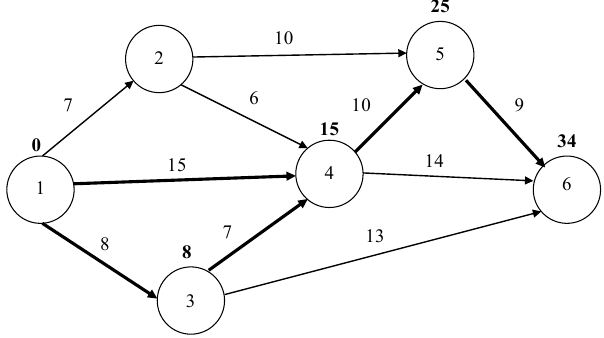
Анализ полученных результатов. Чтобы выполнить работы проекта за директивное время 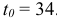, необходимо дополнительно вложить 24 ден.ед. При этом средства распределятся следующим образом: 10 ден.ед. — в работу (1,3), 5 ден.ед. — в работу (1,4), 5 ден.ед. — в работу (3,4) и 4 ден.ед. — в работу (4,5), что приведет к сокращению продолжительности работы (1,3) на 3 дня, работы (1,4) — на 1 день, работы (3,4) — на 1 день и работы (4,5) — на 2 дня.

Сокращение срока реализации проекта за счет вложения дополнительных средств составит 6 ед. времени.

Постановка задачи 2.

Проект представлен сетевым графиком. Для каждой работы известна ее продолжительность 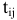и минимально возможное время выполнения 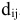. Для сокращения срока реализации проекта выделено В ден.ед. Вложение дополнительных средств 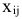в работу 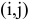сокращает время ее выполнения до 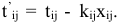. Технологические коэффициенты 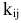известны.

Требуется найти такие 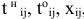чтобы:

• время выполнения всего комплекса работ было минимальным;

• количество используемых дополнительных средств не превышало В ден. ед.;

• продолжительность выполнения каждой работы была меньше заданной величины .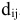

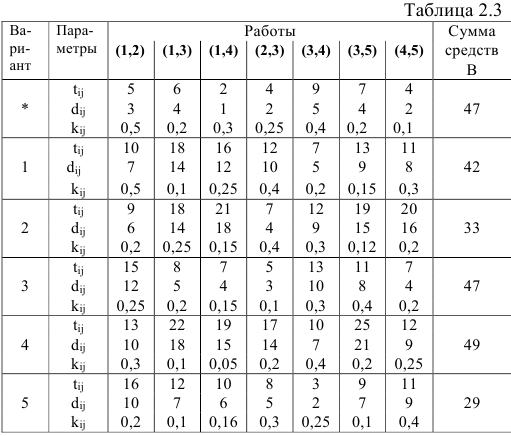
Решение варианта *.

I. Запишем все данные на сетевой график.

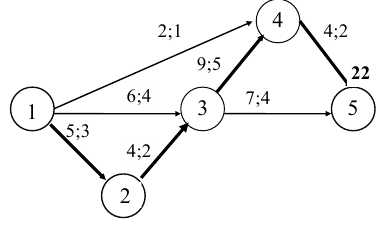
По первоначальному условию 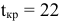, т.е. проект может быть выполнен за 22 ед. времени.

• Составление математической модели задачи.

Чтобы однозначно записать целевую функцию, добавим на сетевом графике фиктивную работу (5,6).

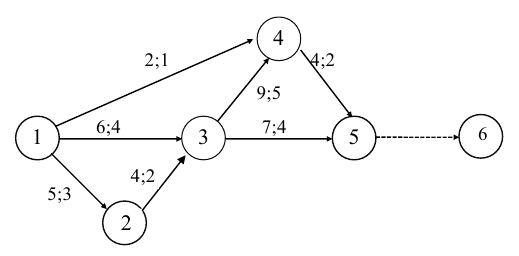
Целевая функция имеет вид

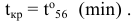
Запишем ограничения задачи: а) сумма вложенных средств не должна превышать их наличного количества:

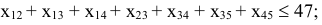
б) продолжительность выполнения каждой работы должна быть не меньше минимально возможного времени:

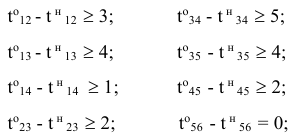
в) зависимость продолжительности работ от вложенных средств:

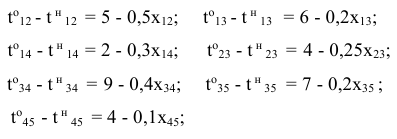
г) время начала выполнения каждой работы должно быть не меньше времени окончания непосредственно предшествующей ей работы:

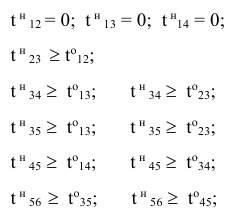
д) условие неотрицательности неизвестных:

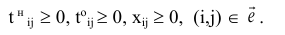
• Численное решение задачи:

Табличную запись математической модели см. табл.2.4.

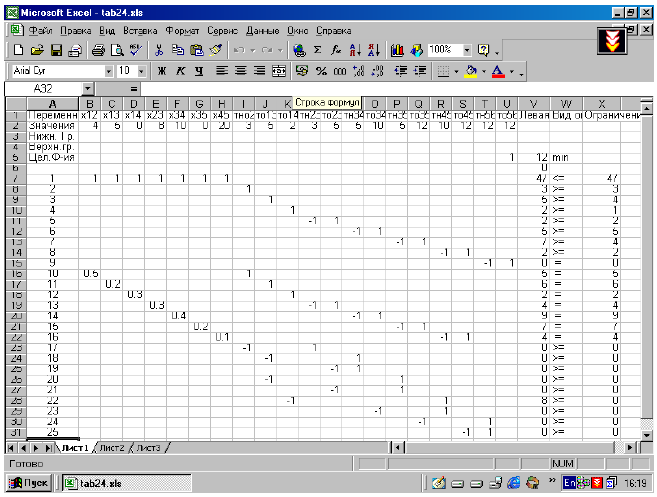
Решив данную задачу средствами EXCEL, получаем следующие результаты:

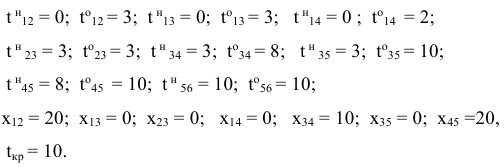
Результаты представим на сетевом графике:

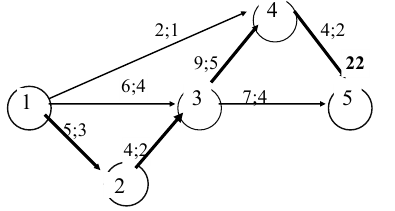
• Анализ полученных результатов. При дополнительном вложении 47 ден.ед., проект может быть выполнен за 10 ед. времени. При этом средства распределятся следующим образом: 20 ден.ед. — в работу (1,2), 10 ден.ед. — в работу (3,4) и 20 ден.ед. — в работу (4,5), что приведет к сокращению продолжительности работы (1,2). Сокращение срока реализации проекта за счет вложения дополнительных средств составит 8 ед. времени.

Контрольная работа №3. Тема: Применение элементов теории игр при принятии управленческих решений

Цель. Используя математический аппарат теории игр определить оптимальное количество продаваемого товара для максимизации среднего денежного дохода Постановка задачи.

На каждой из двух торговых баз ассортиментный минимум составляет один и тот же набор из 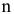видов товаров. Магазины, обозначим их 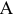и 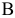, конкурируют между собой. Один и тот же вид товара в обоих магазинах продается по одной и той же цене. Однако товар, поставляемый в магазин 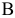, более высокого качества. Если магазин 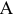завезет с базы товар, отличный от товара, завезенного в магазин 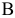, то товар будет пользоваться спросом и магазин 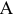от его реализации получит прибыль 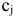денежных единиц. Если же в магазины 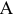и 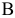завезены товары одинакового вида, то товар в магазине 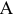спросом пользоваться не будет, поскольку такой же товар, по такой же цене, но более высокого качества, можно купить в магазине , и потому магазин понесет убытки по хранению и возможно порче товара в размере 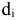денежных единиц.

Требуется формализовать конфликтную ситуацию, построить матрицу игры и дать рекомендации по выбору оптимальной смешанной стратегии при следующих числовых данных:

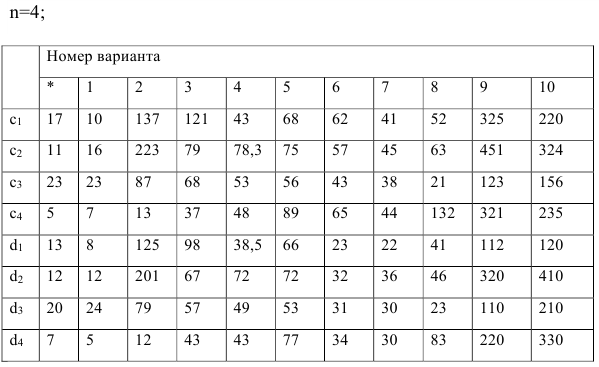
Порядок выполнения работы (на примере варианта*)

• Представим данную ситуацию в виде матричной игры. У руководства магазина 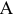четыре стратегии: 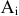— продавать товар 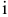-ого вида 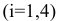. Аналогично у руководства магазина 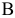стратегии 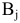-продавать товар 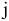-огo вида 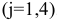. Платежная матрица данной игры примет вид:

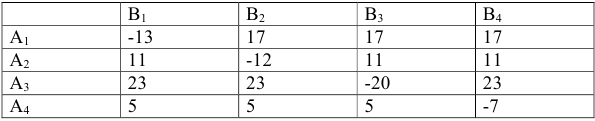
Определим, имеет ли игра оптимальное решение в чистых стратегиях. Для этого рассчитаем верхнюю и нижнюю чистые цены игры.

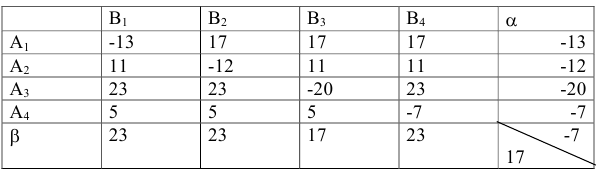
Итак,

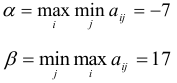
Так как 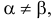то игра не имеет решения в чистых стратегиях. 2. Найдем решение игры в смешанных стратегиях. 2.1. Чтобы свести игру к паре двойственных задач линейного программирования, увеличим все элементы платежной матрицы на 20:

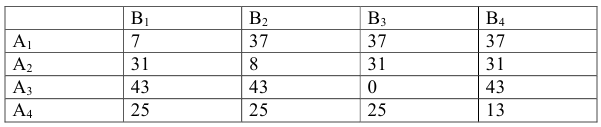
Задача линейного программирования для игрока :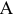

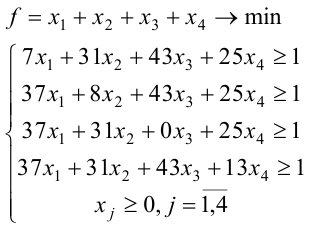
Численное решение контрольной

Решив данную задачу средствами EXCEL, получаем:

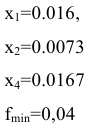
Для определения смешанной стратегии, воспользуемся формулами: Отсюда смешанная стратегия :

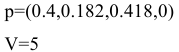
Анализ полученных результатов

Итак, оптимальной стратегией магазина будет продажа товаров в следующей пропорции:

40% товара 1; 18,2% товара 2; 41,8% товара 3;

Средняя прибыль составит 5 д.е.

Контрольная работа №4. Тема: Многономенклатурные модели управления запасами

Цель. Используя математический аппарат теории нелинейного программирования рассчитать оптимальный режим поставок товара для минимизации торговых издержек Постановка задачи.

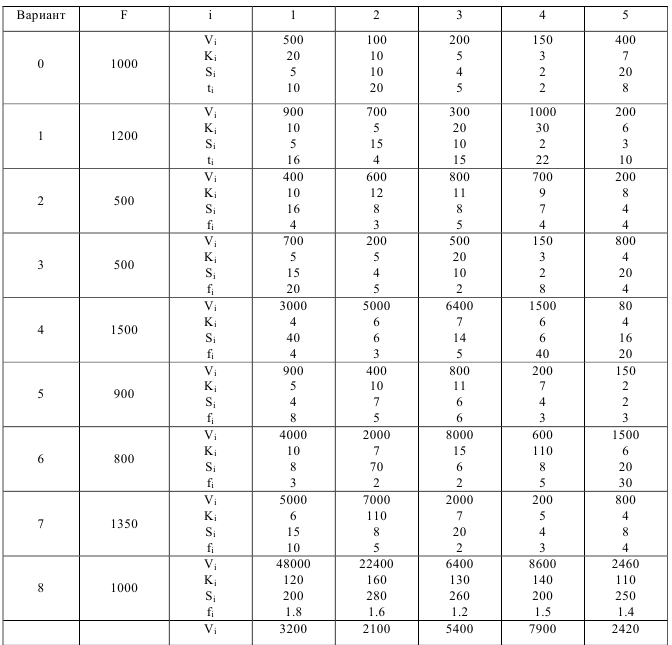
Склад оптовой торговли отпускает 5 видов товаров. Известны потребности 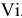, издержки заказывания , издержки содержания 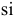, расход складской площади на единицу товара 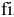, а также величина складской площади торгового зала 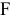. Требуется:

• Определить оптимальные партии поставок при ограничении на максимальный уровень запаса при условии, что все пять видов продукции поступают на склад от разных поставщиков (раздельная оптимизация)
• Продукция поступает из одного источника (полное совмещение заказов). Издержки размещения заказов в этом случае равны средним издержкам индивидуальных издержек заказывания плюс 25% от стоимости организации заказа по каждому продукту.
• Сравнить полученные результаты с действующей системой поставок — один раз в квартал с индивидуальным подходом к каждому продукту (без учета ограничений на складские площади).

Порядок выполнения работы (на примере варианта*)

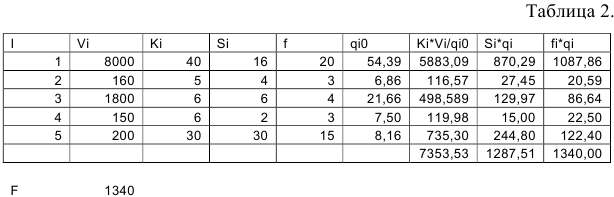
• Раздельная оптимизация вез ограничений на складские площади.) Строим таблицу 1.

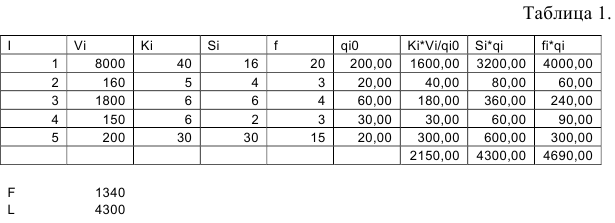
Найдем оптимальные размеры поставок при отсутствии ограничений по формуле Уилсона.

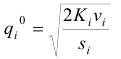
Заносим вычисления в таблицу.

Рассчитаем суммарные расходы при данном плане поставок.

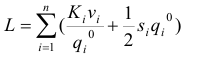
Для этого введем дополнительные столбцы

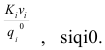
Далее в отдельной ячейке записываем формулу для расчета.

• Раздельная оптимизация с ограничениями на складские площади. Так как ограничение накладывается на максимальный уровень запаса, то 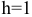. Проверим существенность ограничения на складские площади 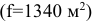. Для этого сравним необходимое количество складских площадей с имеющимся.

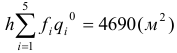
Так как полученное значение больше исходного, то ограничение является существенным.

Для нахождения скорректированных значений составим оптимизационную модель.

Цель — минимизировать суммарные расходы.

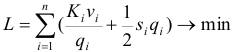
Ограничение вводится на величину складских площадей.

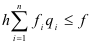
Получили задачу нелинейной оптимизации, которую можно решить средствами ECXEL.

Для расчетов строим таблицу 2. ( Копируем таблицу 1 ниже и ставим значения в столбце 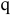равные 1 для того, чтобы начальные значения удовлетворяли области ограничений).

Столбцом значений будет столбец 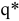. Значение целевой функции находится в ячейке 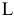. Правая часть ограничения записывается в отдельную ячейку. В программе «поиск решения» задаем параметры -«нелинейная модель», «неотрицательные значения».

• Полное совмещение заказов без учета ограничений на складские площади.

Сначала рассмотрим случай без учета ограничений на складские площади. Издержки размещения заказа равны:

где — среднее значение издержек (в EXCEL рассчитывается с помощью функции СРЗНАЧ).

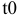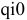Рассчитаем и без учета ограничений.

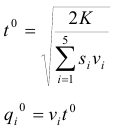
Вычисления делаем в таблице.

Рассчитаем среднегодовые издержки по формуле:

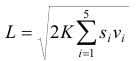
Проверим существенность ограничений на складские площади при полном совмещении заказов.

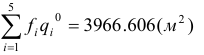
Ограничение является существенным, поэтому для нахождения оптимального периода возобновления поставок воспользуемся формулой:

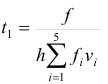
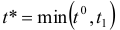
в EXCEL можно использовать функцию МИН. Оптимальные поставки находим по формуле:

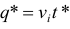
Рассчитываем издержки работы системы при условии ограниченности складских помещений:

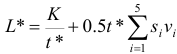
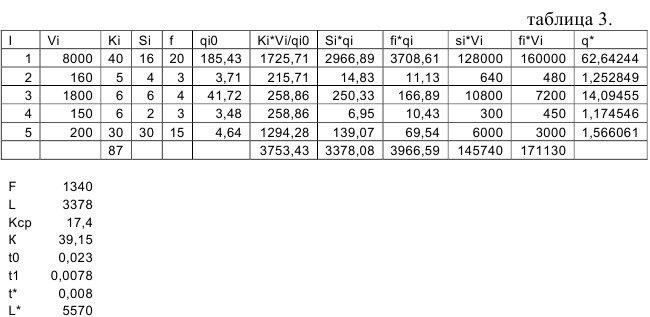
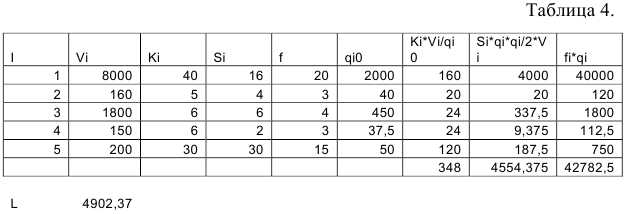
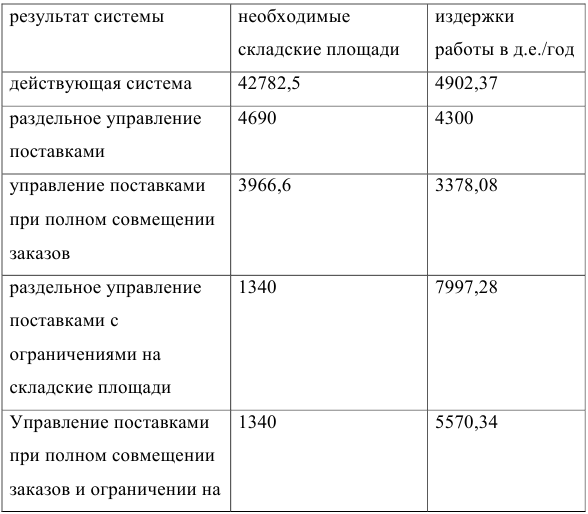
А. Действующая система поставок — один раз в квартал с индивидуальным подходом каждому продукту (без учета ограничений на складские площади). Расчеты проводим в таблице 4.

Так как поставки поквартальные, то

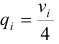
Издержки рассчитываются по формуле:

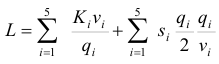
для содержания понадобятся складские площади:

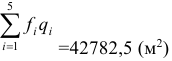
Издержки работы системы составят 4902, 37 д.е.

• сведем полученные результаты в таблицу:

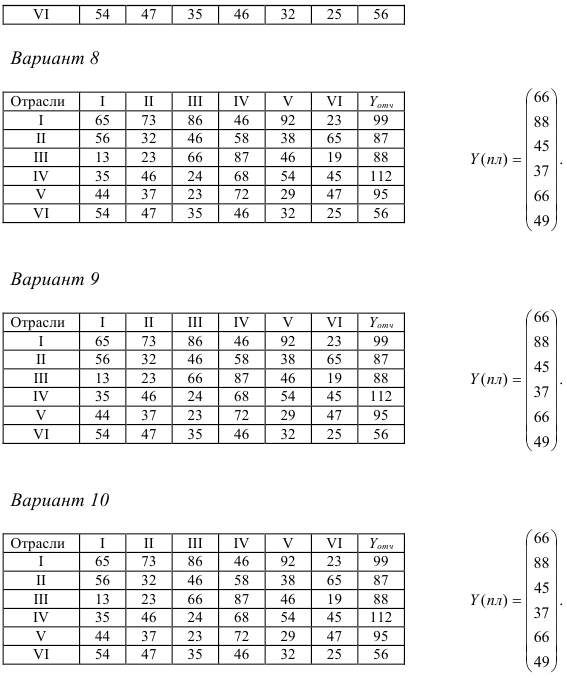
Контрольная работа №5. Тема: Балансовые модели в экономике

Цель. Научиться строить балансовую модель на планируемый период.

Постановка задачи.

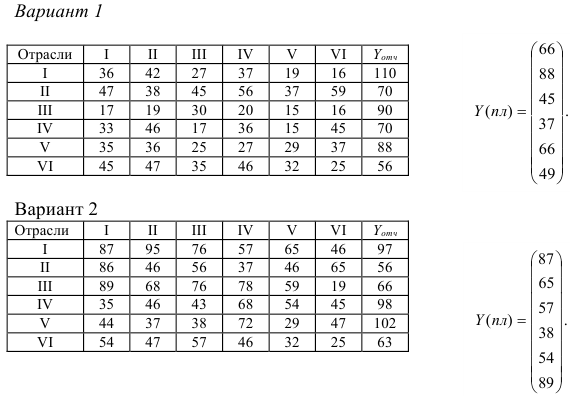
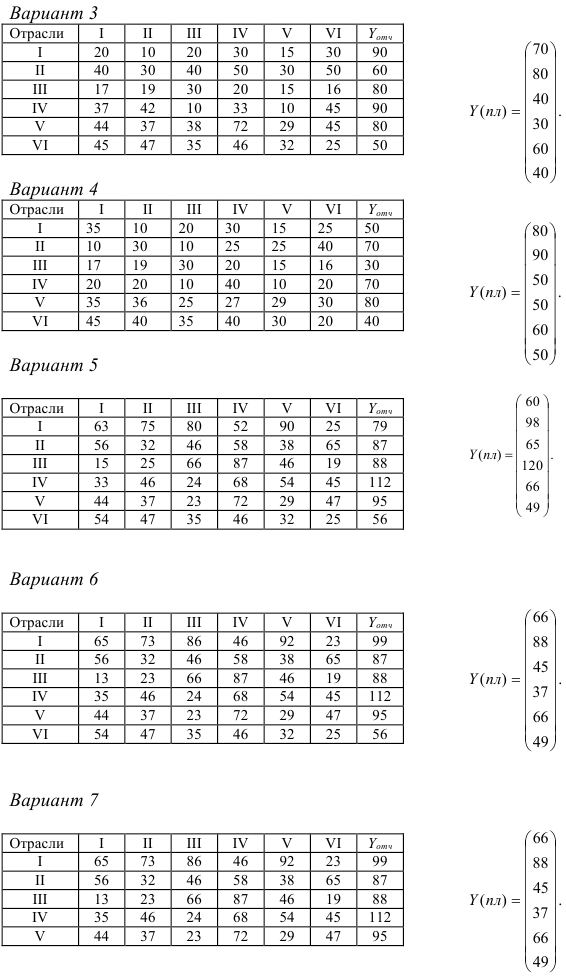
Для шести отраслей за отчетный период известны межотраслевые потоки 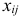и вектор объемов конечного использования 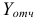. Предполагаем, что в плановом периоде технология производства не изменится.

Требуется:

1) рассчитать плановый межотраслевой баланс при условии, что в плановом периоде известен вектор конечной продукции ;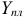

2) привести числовую схему баланса;

3) проанализировать полученные результаты.

Инструкция по выполнению

• Заносим исходные данные баланса в электронную таблицу Excel:

Элементы столбца 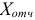рассчитываем по формуле

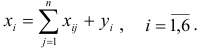
Для этого курсор помещаем в ячейку для 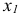, используем функцию СУММ, где в качестве аргумента берем элементы первой строки, затем копируем эту формулу в остальные ячейки столбца 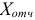. Переписываем полученные значения в строчку 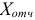внизу, для этого используем формулы, то есть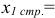 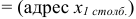и т.д.

• Строим матрицу .

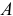Строим таблицу для матрицы размером 6 • 6. В первой клетке записываем формулу например, для 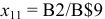(где В$9 — адрес 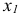в столбце).

Чтобы дальше эту формулу скопировать, в знаменателе перед цифрой в адресе ставим знак $.

Далее эту формулу копируем по матрице.

1. Строим матрицу 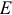. Для этого в свободном пространстве размещаем по диагонали 6 единиц, остальные клетки оставляем свободными.
2. Строим матрицу . Рассчитываем первый элемент 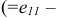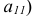, а дальше формулу копируем.
3. Строим матрицу 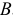, используя функцию МОБР:

а) выделяем массив 6 • 6 под матрицу ;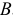

б) вызываем функцию МОБР;

в) вводим в поле Массив диапазон, в котором размещена матрица ;

г) нажимаем Ctrl-Shift и одновременно ОК.

В результате в выделенном массиве появится матрица .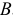

• Строим результирующую таблицу:
  Баланс на планируемый период

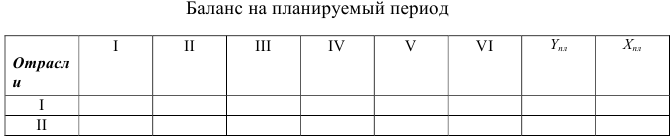
В столбец 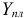вписываем значения 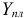из условия. Столбец 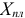и рассчитываем с помощью функции МУМНОЖ:

а) выделяем массив (столбец );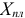

б) вызываем функцию МУМНОЖ;

в) вносим данные: Массив 1 — матрица В, Массив 2 — вектор ;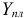

г) Ctrl-Shift-OK одновременно.

• Переписываем значение 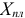вниз в строку (используя формулы).
• Рассчитываем элементы таблицы 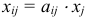, (например, 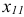= В9 • BS28). Опять в адресе 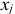перед цифрой ставим $ и затем копируем формулу в нужные клетки таблицы.
• Рассчитываем валовую добавленную стоимость 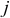-х отраслей:

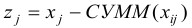
• Проверяем, выполняется ли балансовое соотношение

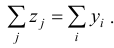
• Рассчитываем балансовое соотношение и заносим в правую нижнюю клетку

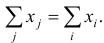
• Анализируем полученные результаты.

Контрольная работа № 6. Тема: Модели анализа инвестиционных проектов»

Цель. Используя математические методы анализа инвестиционных проектов и модели целочисленного программирования оценить эффективность инвестиционного проекта и построить оптимальный инвестиционный портфель Постановка задачи 1.

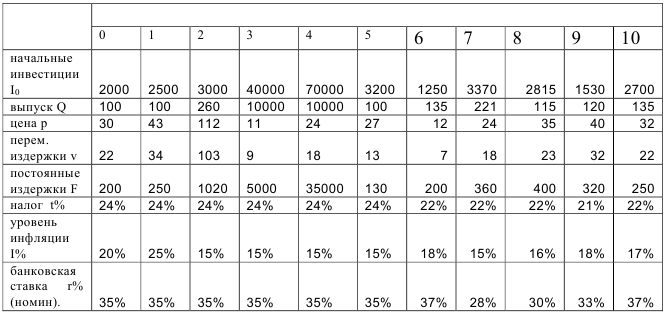
Предприятие рассматривает возможность производства нового вида продукции. Начальные инвестиции в проект составляют 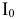млн. д.е., планируемый выпуск продукции — 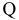в год, ожидаемая цена единицы продукции 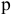д.е., переменные издержки в расчете на единицу — 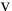д.е., постоянные издержки — 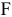млн. д.е. в год. Проект рассчитан на 6 лет. Налог на прибыль равен 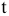%. Ставка дисконтирования денежных потоков проекта — 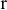%. Уровень инфляции — 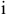% в год. Требуется:

1. Рассчитать основные показатели эффективности инвестиционного проекта.
2. Определить точку безубыточности проекта для следующих переменных параметров:

• выпуск продукции
• цена единицы продукции
• переменные издержки
• постоянные издержки
• налоговая ставка.

Инструкция по решению.

Оценка проекта выполняется в несколько этапов:

1. Расчет исходных показателей по годам
2. расчет показателей эффективности
3. Расчет точек безубыточности.
4. анализ полученных результатов. Этап 1. Строим таблицу данных. Этап 2. Строим электронную таблицу

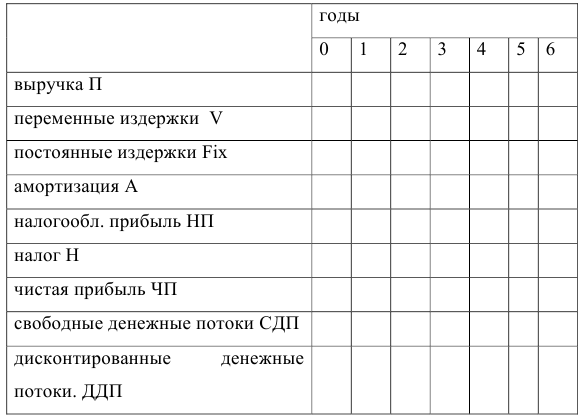
Выручка 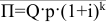, где — номер соответствующего года, в таблице -номер столбца.

переменные издержки 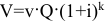постоянные издержки 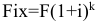амортизация 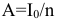налогооблагаемая прибыль 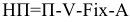налог 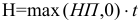рассчитывается с помощью встроенной функции МАКС.

Чистая прибыль

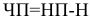
Свободные денежные потоки

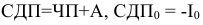
Дисконтированные денежные потоки

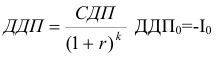
Записываем эти формулы в таблицу: формулу записываем в соответствующую ячейку первого года, указав адреса ячеек с данными, затем копируем ее в клетки по годам. Чтобы сохранялись адреса постоянных ячеек, перед из буквами и цифрами в адресе ставим знак $. ЭтапЗ.

• Чистая приведенная стоимость

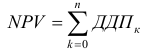
Для расчета воспользуемся математической формулой СУММ. В качестве аргумента выбираем данные строки ДДП, начиная с нулевого года.

• Внутренняя норма прибыли рассчитывается при помощи финансовой функции ВЫДОХ.

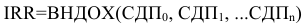
Ставим курсор в ячейку для 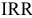, вызываем функцию ВЫДОХ и выделяем строку СДП.

• Показатель рентабельности

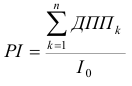
Пишем формулу в ячейку для 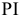аналогично предыдущим пунктам, но для функции СУММ в качестве аргумента берем данные строки ДДП, начиная с первого года.

Этап 4. Делаем экономический анализ полученных результатов

Этап 5. Проводим анализ безубыточности проекта.

Указание. Под точкой безубыточности проекта понимают такое значение параметра 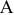, при котором .

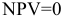Анализ безубыточности проводится с помощью сервис — подбор параметра.

Например, для того, чтобы рассчитать точку безубыточности для параметра 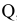, задаем:

• установить в ячейке 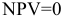значение =0, изменяя значения ячейки «адрес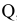

Рассчитанное значение выписываем и возвращаем таблицу в исходное состояние.

Далее проводим анализ безубыточности для остальных параметров. Этап 6. Составляем отчет по работе.

Возможно эти страницы вам будут полезны:

• Экономико-математические методы задачи с решением и примерами
• Решение задач по ЭММ
• Решение экономико математических методов
• Помощь по экономико математическим методам
• Курсовая работа по экономико математическим методам
• Заказать работу по экономико математическим методам